Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Томский Государственный Университет Систем Управления и Радиоэлектроники

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Математика.-7

.pdf

Скачиваний:

Добавлен:

05.02.2023

Размер:

2.74 Mб

Скачать

☆

<<< < Предыдущая 12 / 122 3 4 5 6 7 8 9 10 11 12 > Следующая >>>

Интгерал по

вычисляется с помощью тригонометрической

подстановки
2
2 d sin d
0	0

2 

R sin t
R	2	sin	2

		2
.	2		d			sin
.	2		d			sin
		0			0
t		R	2	R			2	sin
t		R		R				sin

		R		R
d			2	R	2
			2		2
		0
2	t	R cos tdt
	t	R cos tdt

	2	d
	2


		cos				2
2 2						R
2 2					0	R
							4
						0

8R		2		t cos			tdt
8R	4	sin	2	t cos		2	tdt
	4		2			2
		0

sin	2	t	1	sin			2	t	cos tdt		=
sin		t	1	sin				t	cos tdt		=
										2
					2					2
	8R		4			sin 2t
=	8R									dt	=
					0			2
					0


2R		2		2tdt
2R	4	sin	2	2tdt
	4		2
		0

				cos 4t
		2
= 2R	4		1		dt
		0		2
		0

	2						2
												2
		1 dt						cos 4t dt	= 2 R4		sin 4t		1 2 R 4 .
2R 4											sin 4t	=
2R 4												=
		2						2		4	8		2
		2						2		4	8		2
	0						0					0
Ответ.	1		2	R	4	.
			2		4
	2
	2

Задача 6. Вычислить тройной интеграл по 1/8 части шара в 1-м

октанте от функции	f (x, y, z) xy	2	.

Решение. Строение части шара такое же как в задаче 2. А вот в

функции надо будет выразить всё через	,,	по формулам
сферических координат.

		1
2	2	1		sin d
	d	d sin cos sin sin	2	sin d
		2	2
0	0	0

		1
2	2	1
	d	d	5	sin	4	sin	2	cos d
	d	d		sin		sin		cos d
0	0	0

далее, мы видим, что все

множители зависят только от различных переменных, поэтому можно вынести их в соответствующий интеграл и считать не как вложенные действия, а как произведение.

							1
2				2			1
	sin	2	cos	d	sin	4	d	5	d
	sin		cos	d	sin		d		d
0				0			0

. Здесь в первом интеграле -

подведение под знак дифференциала, во втором двукратно применим формулу понижения степени, а в третьем всё очевидно, там только степенная функция.

2 sin 2

1
1	sin	3
		3
3
3			0
			0

				2	1 cos 2				2
d (sin )										d
d (sin )										d
			0			2

2	2	1						1
2		1				2	d	1		=
		4	1 cos 2				d	6		=
	0	4						6
	0

	1		1
	1	6		=
		6	0	=
	6


1		1	1	2
1		1	1	1 2 cos 2 cos	2	2 d
					2

3		6	4	0
				0

	=	1
	=	72
		72

	1
	72
	72

	2
	2

		1 2 cos 2
0
0
			sin 2
		2	sin 2		2
	0				0
3			=	3	.
2		2	=	288	.
2		2		288

1 cos			4
		2
		2

	1	2
	2
	2	0
		0

Ответ.


	d

	1	sin
	8	sin
	8
	3
	288


4		2

	0
	0

1		0	1	0
		0		0
72	2		2 2

первой формулой.

Практика № 2.

Криволинейные интегралы 1 рода Задача 7. Вычислить криволинейный интеграл 1

радиуса 1, на которой задана скалярная функция

рода по окружности

F (x, y) x	2	.

Физический смысл. Можно представить таким образом: на проволоку, выполненную в виде окружности, напыляют какие-то частицы (тогда плотность вполне может даже обращаться в 0 в некоторых точках, ведь это плотность не самой проволоки, а напылённого вещества).

Решение. Вспомним основные формулы из лекций, для параметрически или явно заданной кривой в плоскости.

(1)
(1)
	L
(2)
(2)
	L

F dl




(x(t), y(t))	(x (t))	2

(x, f (x))	1 ( f (x))		2

( y (t))	2	dt
( y (t))		dt
dx .

Решим эту задачу двумя способами, и увидим, что бывают ситуации, когда оба способа вполне применимы и уровню по сложности почти одинаковы.

Способ 1. Зададим окружность параметрически и воспользуемсяx cost, y sin t - параметрически заданное

движение по окружности радиуса 1, где

[0,2

]

При этом x							sin t, y					cost .			F		(x, y) x		2	cos	2	t .
																			2		2

			2														2			2		1 cos 2t
Тогда			cos			2	t	( sin t)			2		(cos t)	2	dt		= cos	2		tdt =		1 cos 2t	dt	=
						2					2			2				2
																						2
			0														0				0	2
			0														0				0
1		2		1				2		1		(2 0) (0 0) = .
1	t	2		1	sin 2t				=	1

2		0		2				0		2
		0


Способ 2. Зададим окружность явно и воспользуемся первой

формулой. В данном случае y																1 x2 , из-за симметрии фигуры
можно вычислить для верхней полуокружности и удвоить.

F (x, y) y через через x .


x	2	, не зависит от y , поэтому в ней

x . А в общем случае надо ещё и			F (
При этом x [ 1,1].

не нужно пересчитывать x, y(x)) - выразить только

f (x)	1 x	2

f	2x
		2
2	1 x

. Тогда

	1
2
2
	1

x	2		1 ( f (x))	2	dx

	1					x	2		1		1 x	2		x	2	1			1
2 x		2		1		x		2 dx	= 2 x	2	1 x			x		2 dx = 2 x	2		1		2 dx	=
		2								2							2
						x					1 x	2		x					x
	1				1	x			1		1 x		1	x		1		1	x
	1								1							1
	1		x	2
2			x		dx	. Далее воспользуемся заменой (известной из 2-го


	1	1 x			2
	1	1 x
семестра), с целью устранить корень.													x sin t dx costdt							, при

этом, чтобы не появлялся знак модуля, лучше даже свести всё к 1-й четверти, для этого можно воспользоваться тем фактом, что функция

чётная, и записать интеграл так:

Если

x [0,1]

то соответственно

1		x	2
2		x				dx
2	1 x				2	dx
1					2
1
t [0,				] .
t [0,		2		] .
		2

1 4

x	2
x
1 x		2
1 x

x 2

sin 2 t

2 sin 2 t

= 4

cos tdt

= 4

cos t

cos tdt = 4

sin 2 tdt =

1 x

sin

1 cos 2t

= 2 (

0) (0 0)

= .

sin 2t

dt = 2 t

Ответ. .

Задача 8.

Вычислить массу проволоки, выполненной в виде графика

f (x) ln x , плотность которой

F (x, y) x

, где x [1,

2] .

Решение.

Здесь кривая задана явно, так что надо решать по формуле

F dl F (x, f (x))

1 ( f (x)) 2

dx . Очевидно, f (x)

, тогда

2							1				2					x		2		1
		x	2		1		1			=			x	2		x				1			=
			2					2 dx						2								dx
							x	2 dx											x	2		dx
1							x				1								x
1											1
1		2										1		2
1				x	2	1		2xdx			=	1				x	2				1 d (x			2
					2												2							2
2												2
2		1										2		1
		1												1
1	3			3 2			2		=	3			2		2 .
3	3			3 2			2		=	3			3		2 .
3													3
Ответ.						3		2		2 .
Ответ.						3		3		2 .
								3

2
	x
1
1)

x 2

=1 2

2 3

1 dx

x 2

13 2 = 1

Задача 9. Найти линии (спирали) вx cost, y sin t,

криволинейный интеграл 1-го рода по винтовой пространстве, заданной параметрически:

z t , рассматривая 1 виток, т.е. t [0,2 ] ,

если скалярная функция	F (x, y, z) 2z x	2

Решение. Нужно воспользоваться формулой

y	2	.

для 3-мерного случая:

b
	F (x(t), y(t), z(t))										2					2					2	dt .
	F (x(t), y(t), z(t))						(x (t))					( y (t))					(z (t))					dt .
a
Вычислим производные: x sin t, y cost, z 1 .
В функции			F		нужно все переменные полностью выразить через
В функции					нужно все переменные полностью выразить через
			2	2t cos										t
Получаем:								2	t sin				2		( sin t)			2	(cos t)				2	1	2	=
Получаем:									t sin						( sin t)				(cos t)					1	dt	=
			0
2										2				2			2 4			2 .
2t 1			2dt			=			2		t								2
									2										2
							2 t							=
0										0				0
0		2 4				2 .
Ответ.					2
Ответ.

Поверхностные интегралы 1 рода

						2
Формула из теории:		F dS		F (x, y, f (x, y))
Формула из теории:		F dS		F (x, y, f (x, y))	1 f x
	S		D

f
	2
	y

dxdy

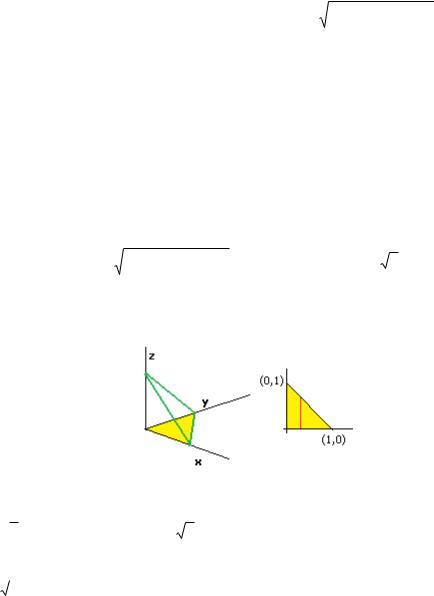
Задача 10. Найти поверхностный интеграл 1-го рода от скалярной функции F (x, y, z) xyz по треугольнику с вершинами (1,0,0), (0,1,0)

и (0,0,1).

Решение. Во-первых, нужно получить явное уравнение плоскости, в которой расположен треугольник. Пусть z kx my c . Подставим

точку (0,0,1), получим

c 1.

Подставим (1,0,0), получим Подставим (0,1,0), получим Итак, уравнение плоскости:

0 k 0 0 z f



0 1, откуда

m 1, откуда , y) 1 x y

k 1.

m 1.

Тогда		1	,		1.
	f x			f y

F (x, y, f (x, y))	1 f x		f y		dxdy =	xy(1 x y)	3dxdy , где
		2		2

D						D

- проекция исходного треугольника на плоскость, т.е. треугольник с вершинами (0,0), (1,0) и (0,1) в плоскости, ограниченный сверху

линией

y 1 x .

Расстановка пределов в таком двойном интеграле была подробно изучена в прошлом семестре:

1 1 x

3 dx xy(1 x

0 0

	1		y	2


3 dx x(1		x)
3 dx x(1		x)	2

0

						1	1 x
y)dy =				3			dx		(x(1 x) y xy	2	)dy
										2

						0		0
1 x		y	3		1 x
1 x			3		1 x
	x							=
	x							=
	3
0	3				0
0					0

1	1	1
	1	1		x)	3	dx
3			x(1	x)		dx
0	2	3
0

3	1
3	x(1 x)	3	dx
		3
6
6	0
	0

. Далее, чтобы уменьшить

количество арифметических действий при раскрытии скобок, можно сделать замену

t 1

	t
3	1
3
6	0
	0

, при этом получим										3
, при этом получим										6
										6
		dt		3	t		4	t	5		1
				3	t		4	t	5
t	4		=
t			=	6		4		5

											0
											0

0
(1 t)t		3	( dt)
(1 t)t			( dt)
1
=	3	.
=	120	.
	120

		1
	3	1
=	3		(1 t)t 3dt			=
=	6		(1 t)t 3dt			=
	6	0
		0
Ответ.				3	.
Ответ.				120	.
				120

Задача 10. Найти поверхностный интеграл 1-го рода от скалярной

функции F (x, y, z) x y 3z

по полусфере радиуса 3 в верхней

полуплоскости.

Решение. Уравнение сферы

, тогда явное уравнение

данной полусферы

f (x, y)

9 x

, соответственно

2 y

f x

9 x

, f y

F (x, y, f (x, y))

dxdy

1 f x

f y

x y 3

9 x

dxdy =

9 x

x y 3

9 x

dxdy

, где

- проекция этой

9 x

полусферы на плоскость Оху т.е. круг радиуса 3:

9 .

Разобьём на 2 слагаемых, причём во 2-м корни сокращаются:

			x y			dxdy 9							dxdy. В первом перейдём к полярным

3				2
	D		9 x	2	y	2					D
	D		9 x		y						D
координатам, а во втором интеграл от 1, т.е. это просто площадь
круга.
			x y												2				3		cos sin
			x y			dxdy 9							dxdy = 3				d				cos sin			d 9	3	2
3																										2
3																							2
	D		9 x	2	y	2					D					0			0			9	2
	D		9 x		y						D					0			0			9
	2								3				2
=	3		(cos sin )d												d 81				=


		0							0	9					2
		0							0	9
	3 sin cos						2	3				2
=							2								d 81			=		0 81		= 81 .
							0
										9				2
								0						2
								0

интеграл по получается 0, поэтому в первом слагаемом интеграл по вычислять уже не нужно.

Ответ. 81 .

Криволинейные интегралы 2 рода
Задача 12.		F x z, y, y z по перемещению
Найти работу векторного поля		F x z, y, y z по перемещению
точки по винтовой линии (спирали), заданной уравнениями
x a cos t, y a sin t, z t ,	t		0,		.
	t		0,	2

Решение. Требуется вычислить такой интеграл:

P(x(t), y(t), z(t)) x (t) Q(x(t), y(t), z(t)) y (t) R(x(t), y(t), z(t)) z (t) dt

или его краткий вид:

	a
Производные: x	a
Тогда

P dx Q dy

a sin t, y a cos t,

R dz .

z 1

(a cos t 0

Заметим,

что

(a sin
a	2	sin t

t) cos

(

a sin t) (a cos t) (a sin t t) dt

присутствует со знаками + и

–, сокращается.

at sin t a sin t t dt 0

a t sin tdt 0

a sin tdt 0

tdt 0

, в первом из них

применим интегрирование по частям:																						u t, v	sin t, u	1, v
применим интегрирование по частям:																						u t, v	sin t, u	1, v
						2															2	2
																				t
a	t cos t		2				cos tdt							2						t		=
a	t cos t						cos tdt			a cos t												=
		0											0							2
																				2
						0																0
							2					2														2
a	(0 0) sin t						a 0 1							= a (0 0) (1 0) a
a	(0 0) sin t						a 0 1				8			= a (0 0) (1 0) a											8
						0					8														8
					2
					2
Ответ. 2a .
				8
Вариант этой задачи для t 0,2																	(домашнее задание).
		2			2							2							t 2 2
	t cos t 0			cos tdt						a cos t 0
a	t cos t 0			cos tdt						a cos t 0								2 0
						0												2 0
= a t cos t									a cos t							t		2		2
			2					2			2							2
			2	sin t				2			2											=
			0	sin t				0			0						2					=
			0					0			0
																				0
												4								0
a (2 0) (0 0) a 1 1												4			2
															2
													2						= 2 a 2 2 .
													2

cos t .


	2
2a	8
	8


Практика № 3.
Задача 13.					2x2		y, x y 2 по перемещению
Найти работу векторного поля
Найти работу векторного поля				F
точки по участку параболы y x					2	, где	x 0,1 .
точки по участку параболы y x						, где	x 0,1 .
Решение. Здесь используем формулу для явно заданной кривой:
			b
		, dl	P(x, f (x)) Q(x, f (x)) f (x) dx .
	F	, dl	P(x, f (x)) Q(x, f (x)) f (x) dx .
L			a

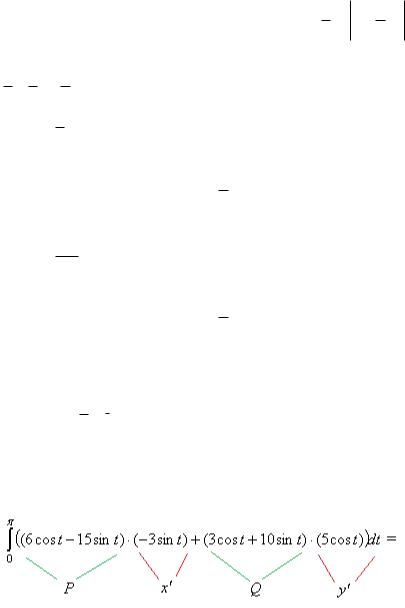
Все

надо

y , которые встречаются в записи компонент векторного поля,
выразить в виде x	2	. Очевидно также, что	f	2x Итак:

1	2x
	2x		2
			2
0
5		1		=
3		3		=
3		3

Ответ.

	x	2

	4
	3
	4	.
	3

) (x x	4	) 2x dx

	1
=
=
	0

5x	2	2x	5	dx

5		1	2		1
	x	3		x	6

3			6
		0			0

Задача 13-А (домашняя аналогичная № 13).

Найти работу векторного поля

F x

, x

по перемещению

точки по участку кубической параболы

y x

, где

x 0,1 .

Ответ.

118

105

Задача 14.
Найти работу векторного поля F 2x 3y, x 2 y по перемещению
точки по половине эллипса, заданного параметрически:
x 3cost, y 5sin t ,	x 0, .

Решение. Здесь используем формулу для параметрически заданной

кривой:

F , dl

b P(x(t), y(t)) x (t) Q(x(t), y(t))

y (t) dt

L	a
При этом учитываем, что x		3sin t, y	5cost . При этом все	x	и

y , которые встречаются в записи компонент векторного поля, надо
выразить в виде x 3cost, y 5sin t .

<<< < Предыдущая 12 / 122 3 4 5 6 7 8 9 10 11 12 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
05.02.20232.61 Mб4Математика.-2.pdf
#
05.02.20232.05 Mб3Математика.-3.pdf
#
05.02.20232.49 Mб3Математика.-4.pdf
#
05.02.20233.03 Mб3Математика.-5.pdf
#
05.02.20232.78 Mб3Математика.-6.pdf
#
05.02.20232.74 Mб5Математика.-7.pdf
#
05.02.20233.16 Mб4Математика..pdf
#
05.02.2023584.83 Кб53Математическая логика и теория алгоритмов.-1.pdf
#
05.02.2023886.2 Кб7Математическая логика и теория алгоритмов.-2.pdf
#
05.02.2023671.92 Кб5Математическая логика и теория алгоритмов.-3.pdf
#
05.02.2023482.94 Кб5Математическая логика и теория алгоритмов.-4.pdf