Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Томский Государственный Университет Систем Управления и Радиоэлектроники

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Математика.-7

.pdf

Скачиваний:

Добавлен:

05.02.2023

Размер:

2.74 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 1211 12 > Следующая >>>

	x 1		if	x ( 1,0)
Задача 113. Найти ряд Фурье для	f (x)	1	if	x (0,1)

Решение. Здесь функция не является чётной либо нечётной, поэтому надо будет искать все коэффициенты.

При этом, на левой и правой части интервала надо считать отдельно, ведь там функция задана по-разному.

	0	1
a0	(x 1)dx 1dx
	1	0
	0
an (x 1) cos n xdx
	1

x
	2

=
	2
	2
1
cos
0

	0	1	1			3		a		3
	0

x	x		=		1 1		,		0
		0		2		2		2		4
	1							2		4



n xdx . Первый интеграл вычисляется

методом «по частям», второй просто в один шаг.

Кстати, для удобства вычислений можно раскрыть скобки и объединить так:

0 x

0 x cos n xdx

1 1 cos n xdx cos1

0		1
	cos n xdx		cos n xdx	=
	cos n xdx		cos n xdx	=
1		0
n xdx. Тогда интеграле по частям остаётся не

скобка, а только

u		1,

cos

n x

1 n

sin

n x

. Тогда

0	1
x cos n xdx cos n xdx
1	1

	x		0	1	0		1	1
=		sin n x				sin n xdx		sin n x
	n			n			n

			1		1			1

	1					1	0				0 0					1			0
	1					1	0				0 0					1
=		sin( n )					sin n xdx						=		0			cos n x	0
=	n	sin( n )			n		sin n xdx				n		=		0	2	2	cos n x	0
	n				n		1				n					n			1
							1
cos 0 cos( n )						1 cos(n )				1		( 1)		n
cos 0 cos( n )				=		1 cos(n )			=	1		( 1)			.
	n	2	2	=			2	2	=		n	2	2		.
		2	2				2	2				2	2
							n
	0						1					0						1
bn (x 1) sin n xdx sin n xdx = x sin n xdx																		sin n xdx
	1						0					1						1

101

В первом

u 1,

v sin

n x

	v	1
	v	n
		n

cos n x

. Тогда

x		0	1	0	1	1
	cos n x			cos n xdx		cos n x
n			n		n
		1		1		1

cos n	1		0
			sin n x
n	2	2

	n		1

		cos n cos n
		n
		n

=	( 1)n	0 0	=	( 1)n 1
	n			n

Ответ. Ряд Фурье:

3		1	( 1)		n

4		n	2	2
	n 1

	( 1)	n 1
cos n x	( 1)		sin
cos n x	n		sin
	n

n x

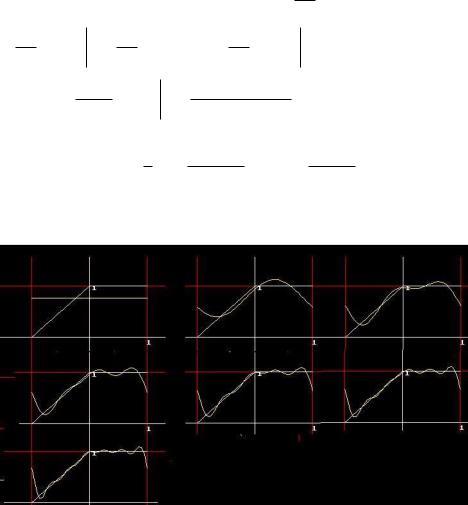
Чертёж к этой задаче, получившийся в результате работы программы на Паскале. Видно, что чем больше n, тем более плотно кривая, соответствующая частичной сумме, огибает ломаную.

102

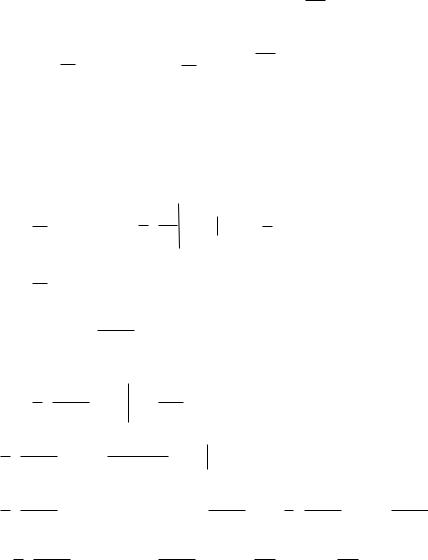
Комплексный ряд Фурье.

	in x
f (x) c0 cn e	l
f (x) c0 cn e
n

in x

Где

f (x)dx ,

dx .

f (x)e

Задача 114. Разложить в комплексный ряд Фурье функцию

f (x) x 1

на

1,1 .

Решение.

Здесь l 1. Ищем коэффициенты Фурье для системы

in x

0 2 = 1.

1)dx

x 1

1)e

in x

, здесь вычисляем по частям,

u x 1

in x

u 1

in x

e in

1 2

		2		in
			e	in
			e
	in
	in

1		2		e	in
		in		e
2		in

(e	in		e	in	)		2i
									=
		2i				n	2	2	=
							2	2

			1			in			i
0		=			e	in		=
0		=	in		e			=	n
			in						n

e	in

2	e	in			2i
in					2	2	sin n
				n

=	i		(cos n i sin n )
	n

	i		in x		i( 1)	n
=		(( 1)n 0) . Тогда c0 cn e	l	= 1			ein x .
	n				n
		n		n

103

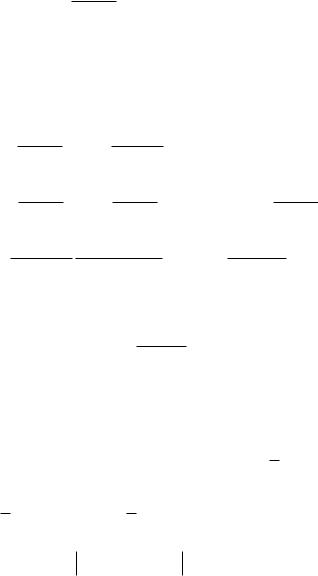
Ответ.

	i( 1)	n
1	i( 1)	e	in x
			in x
	n
n	n
n
n 0

Если мы дальше преобразуем экспоненты в комплексной степени, то

получим действительную форму, т.е.

тригонометрический ряд.

Объединим элементы с номерами

n,n . Тогда нумерация будет уже

только по натуральным числам.

i( 1)

in x

n 1

i( 1)

in x

n 1

( 1)

in x

2( 1)

n 1

= 1

sin n x .

n 1

Кстати,

если отнять 1, то получилась бы функция

f (x) x , а ведь для

неё получали именно такое разложение в ряд Фурье в примере на

лекции (см. стр. 118):

	2( 1)	n 1
		sin
	n
n 1

n x

Задача 115. Разложить в комплексный ряд Фурье

1		( 1,0)
f (x)	1	(0,1)

																							1	1
Решение.						Функция нечётная, поэтому c0																	1			f (x)dx
																							2

																								1
																								1
			1	1										1			0					1
cn			1		f (x)e			in x		dx			=	1		( 1) e				in x	dx 1 e				in x		dx
								in x												in x					in x
			2											2
			2	1										2	1							0
				1											1							0
	1			1		e in x			0					1		e in x			1
																			=
			in									in							=
	2		in						1			in							0
1		1 ein x					e in				1				1			(1 ein x ) (e in					1)
														=													=
2			in					in							2					in
2			in					in							2					in

104

in x

1 2 e

in x

2 (e

in x

)

2 2

1	2 2 cos n		1 cos n		1 ( 1)
		=		=
	in		in		in
2

		1	( 1)	n
		1	( 1)	e
				in x
Ряд:	n		in		. Впрочем,
			in

	n 0

заметим, что при чётном n

коэффициенты равны 0. Тогда можно так задать индексацию, чтобы

учесть только все нечётные номера. Для любого целого числа,	2n 1
нечётное. Тогда можно записать в таком виде:

		2
		2			e
					i (2n 1) x
n	i(2n 1)
n
			1	( 1)		n
			1	( 1)			e
							in x
Ответ.		n			in
					in

		n 0

	2
=		ei (2n 1) x .

n i(2n 1)

Практика № 15.	17.12.2018
Задача 116. Разложить функцию		f (x)
Фурье на [ 1,1] .

Решение. Функция является четной, bn

x	2

0

в тригонометрический ряд

	1
a0	x	2	dx
a0	x		dx
	1

1
2 x	2	dx
2 x		dx
0

= 2

x	3	1


3		0

= 23 .

105

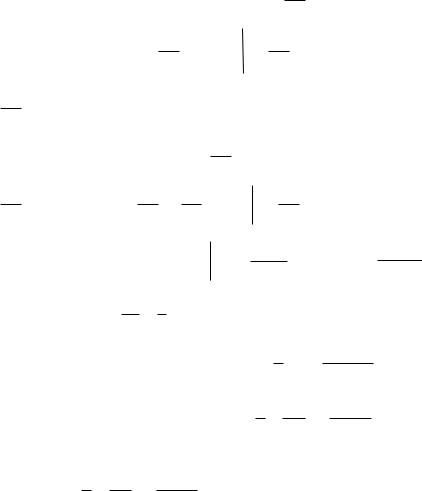
1
an x	2	cos n xdx
an x		cos n xdx
1

в силу чётности равно

1 2 x 2

cos n xdx

, такой

интеграл можно найти с помощью интегрирования по

Сначала u1 x	2				1
		, u1	2x , v1	cos n x, v1		sin n x
					n

частям в 2 шага.

2 x 2 cos n xdx

		2	1		1
x			sin n xdx	2		x sin n xdx

= 2	n			n
	n		0	n	0
			0		0

4 n

		4
		n
		n

x sin n xdx. Затем 2-й шаг,

x, u		1, v		sin n x, v	1	cos n x .
	2		2
				1	n

1	4	x		1	1	1
x sin n xdx =			cos n x			cos n xdx

	n	n			n
0						0
				0

	4		1								1			1						4
					cos n								sin n x				=					cos n 0									=
					cos n					n2			sin n x				=	n2 2				cos n 0									=
	n		n							n2		2		0				n2 2
														0
							n		a
Итак, a				4( 1)				,	a		0	1 ,		b 0 .
				4( 1)
		n
		n			n	2	2		2			3		n
						2	2


																					1					4( 1)						n
Разложение функции в ряд Фурье:																	x	2			1					4( 1)
																		2
																					3						n	2		2
																												2		2
																								n 1
																								n 1
																			1			4					( 1)				n
его можно также записать в виде															x	2			1			4					( 1)
																2
																			3				2					n	2
																							2						2
																									n 1
																									n 1
вынести константы, не зависящие от n,																			за знак суммы.

4( 1)			n
				.
n	2	2

cos n x

cos n x , если

Ответ.

		1	4			( 1)		n
x	2	1	4			( 1)
	2
		3		2		n	2
		3			n 1	n
					n 1

cos n x

Замечание. С помощью этого ряда Фурье можно найти суммы

	1			( 1)n
числовых рядов			и			.
	n	2		n	2
n 1			n 1

106

Подставим

	1	4			( 1)		n
0
	3		2		n	2
				n 1

, то есть

2 n2

n 1 (4 1)

Подставим

1 3


, из чего следует
						n 1
	1	4			( 1)		n
1	1	4			( 1)
1	3		2		n	2
	3			n 1	n
				n 1

( 1)		n			2
( 1)						.
n	2			12



cos n
			, то есть

2	4		( 1)	n	( 1)	n	4		1			1		2
										, из чего следует					.

3	2	n 1		n2			2	n 1 n2			n 1 n2		6

Задача 117. Разложить функцию		1	, x ( 1,0)
Задача 117. Разложить функцию	f (x)
	x 2, x (0,1)

в тригонометрический ряд Фурье на [ 1,1] .

Решение. Найдём все коэффициенты ряда Фурье. Здесь l

	1	перед каждым интегралом не пишется.
	l	перед каждым интегралом не пишется.
	l

поэтому

a0 f (x)dx

0	1
1dx (x 2)dx
1	0

=	x

0	x	2	1	1
			1

			2x

1	2			0
1			0	0

1	1	2
	2

	=	7
	=	2
		2

При этом

1
an	f (
1

	a0	7	. Далее, вычислим все прочие коэффициенты.
2		4	. Далее, вычислим все прочие коэффициенты.
2		4
				0		1
x) cos n xdx =					cos n xdx		(x 2) cos n xdx
x) cos n xdx =					cos n xdx		(x 2) cos n xdx
				1		0

во 2-м слагаемом здесь будет интегрирование «по частям».

u x 2

u 1

v	1	sin( n x)
	n

v cos(n x)

107

1	0	x 2	1	1	1
	sin( n x)		sin( n x)			sin( n x)dx	.

n		n		n

	1		0		0

Теперь получилось 3 слагаемых, в 1-м и 2-м получится каждом, так как там либо sin 0 либо sin n .

0 0 0

0 sin( n )						3sin( n
0 sin( n )						3sin( n
	n						n
	n						n

	0		cos(n ) 1				=
0	0			2	2		=
			n	2	2
			n
	1
bn		f (x) sin n xdx =
bn		f (x) sin n xdx =
	1

) 0				cos(n x)				1
) 0				cos(n x)

				n		2	2
				n				0
								0
( 1)		n	1
( 1)			1		.
n	2		2		.
	2		2

0							1
sin n xdx (x
1							0

2) sin n xdx

во 2-м слагаемом также интегрируем по частям.

u x 2

cos(n x)

u 1

v sin( n x)

x 2

cos(n x)

cos(n x)dx

1 cos(n )

3cos(n ) 2

sin( n x)

теперь 3-е слагаемое содержит

sin 0

sin n

и равно 0.

При этом мы ещё и не различаем

cos(n )

и cos(n )

так как косинус

функция чётная. И то и другое равно

( 1)	n

1 ( 1)n

3( 1)n 2

0 0

( 1)n

2 3( 1)n

1 2( 1)	n
1 2( 1)
n

Итак,

( 1)n 1

1 2( 1)n

. Мы знаем все

n2 2

коэффициенты и теперь запишем ряд Фурье:

108

Ответ.

7		( 1)		n	1		1 2( 1)	n
7		( 1)			1		1 2( 1)
						cos n x
4		n	2		2	cos n x	n
4	n 1	n					n

sin

n x

Задача 118. Разложить функцию																			f (x)		1	, x ( 1,0)
Задача 118. Разложить функцию																			f (x)
																					x 2,		x (0,1)
в комплексный ряд Фурье на																[ 1,1] .
Решение. Здесь									l	1, поэтому							1		перед каждым интегралом это										1	.
Решение. Здесь									l	1, поэтому							2l		перед каждым интегралом это										2	.
			1										0				2l										2		2
		1	1								1		0				1					1				x	2	1
		1									1											1			0	x			1
c0					f (x)dx				=				1dx (x							2)dx	=		x		1			2x	0
c0					f (x)dx				=											2)dx	=							2x
		2									2											2				2
1			1									1					0											0
			1									1					0											0
			1			=		7	.
	1			2		=			.
2			2					4
		1	1										1		0					1
сn		1			f (x)e		in x			dx	=		1		e	in x		dx (x 2)e				in x		dx
							in x									in x						in x
		2											2
		2	1										2	1						0
			1											1						0

Во втором слагаемом интегрирование по частям.

u x 2					v				1			e	in x
													in x
								in
								in
u 1					v e in x
1		1					0			1		x 2						1		1				1
1		1	e	in x						1		x 2			e		in x			1						e		in x			dx			=


	2 in									2		in								in
	2 in						1			2		in						0		in				0
							1											0						0
1		1					0			1		x 2						1		1		1
1		1	e	in x						1		x 2			e		in x			1			e		in x					dx			=


	2 in									2		in								in
	2 in						1			2		in						0		in		0
							1											0				0
1		1					0			1		x 2						1				1										1
1		1	e	in x						1		x 2			e		in x					1							e	in x				=
				in x													in x													in x
	2 in									2		in								i	2	n	2				2
							1														2		2				2
																		0
																		0														0
1		1 ein				3e in					2			e	in			1
																			.
																2		2	.
2		in						in							n	2		2
2		in						in							n

109

Учтём тот факт, что по формуле Эйлера:

e		in			cos n i sin n =															( 1)				n			i0					= ( 1)					n		,
e					cos n i sin n =															( 1)							i0					= ( 1)							,
	e		in			cos n i sin n													=				( 1)				n			i0			=	( 1)						n	.
	e					cos n i sin n													=				( 1)				e			i0			=	( 1)							.
						1 1 e				in						3e		in		2							e		in				1
Тогда																																				=
Тогда						2		in									in													n	2		2			=
						2		in									in													n
1				1 ( 1)				n		3( 1)						n	2					( 1)					n		1
1				1 ( 1)						3( 1)							2					( 1)							1
																																	=
2					in								in										n		2			2					=
2					in								in										n
1				1 ( 1)				n	3( 1)						n		2					( 1)				n		1						1				2( 1)				n	1	( 1)		n	1
1				1 ( 1)					3( 1)								2					( 1)						1						1				2( 1)					1	( 1)			1
																																	=
2								in															n	2				2					=	2							in			n	2		2
2								in															n											2							in			n
1				1 2( 1)n								( 1)n 1
																			.
														2			2		.
2						in							n	2			2
2						in							n
Мы вычислили коэффициент																										cn				и теперь можно записать ряд.
							7				1		1 2( 1)								n				( 1)						n	1
							7				1		1 2( 1)												( 1)							1			in x
Ответ.																																			in x				.
Ответ.																														2		2	e						.
							4		n 1 2								in										n			2		2
							4		n 1 2								in										n

Контрольная работа.

Практика № 16. 24.12.2018 Исправление долгов

110

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 1211 12 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
05.02.20232.61 Mб4Математика.-2.pdf
#
05.02.20232.05 Mб3Математика.-3.pdf
#
05.02.20232.49 Mб3Математика.-4.pdf
#
05.02.20233.03 Mб3Математика.-5.pdf
#
05.02.20232.78 Mб3Математика.-6.pdf
#
05.02.20232.74 Mб5Математика.-7.pdf
#
05.02.20233.16 Mб4Математика..pdf
#
05.02.2023584.83 Кб53Математическая логика и теория алгоритмов.-1.pdf
#
05.02.2023886.2 Кб7Математическая логика и теория алгоритмов.-2.pdf
#
05.02.2023671.92 Кб5Математическая логика и теория алгоритмов.-3.pdf
#
05.02.2023482.94 Кб5Математическая логика и теория алгоритмов.-4.pdf