Кодирование в телекоммуникационных системах.-2

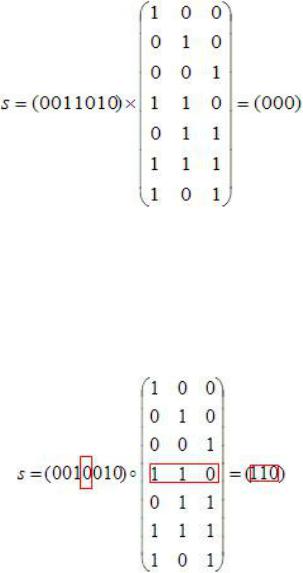
131

Вектор s принято называть синдромом. Таким образом, ошибка будет обнаружена, если хотя бы одна из компонент s не равна нулю.

При передаче информационного слова a = (1010) по каналу без шумавыходной вектор был n = (0011010). Можем убедиться, что в этом случае синдром равен 0.

Рис. 3.6. Получение синдрома для кода (7,4)

Если, например, в кодовом слове произошла одиночная ошибка на четвертой позиции

(r = (0010010)), то синдромом является четвертая строка транспонированной проверочной матрицы.

Рис. 3.7. Нахождение ошибочного бита для кода (7,4)

Перебрав все возможные позиции одиночной ошибки, получим полную таблицу синдромов однократных ошибок - таблицу соответствий номера ошибочного разряда получающемуся при этом синдрому. Таким образом, производится декодирование. Если ошибки найдены, то они соответственно исправляются.

132

Проведение эксперимента и обработка результатов в MATLAB 2015

Задание:

1.Собрать схему

2.Подготовить схемы для реализации кодов Хэмминга (7,4) и (15,11)

основываясь на примере, представленном в отчете.

При коде (7,4) в параметрах кодера и декодера MessagelengthK, or M- degreeprimitivepolynomial: устанавливается gfprimfd(3,'min'), а при коде (15,11) gfprimfd(4,'min').

3. Для полученных кодов изменять вероятность ошибки в пределах от 0 до 1 (не менее 4-х точек) и снимать с дисплеев полученные входные последовательности,

закодированные последовательности, декодированные последовательности и ошибки.

4. Построить графики зависимости числа обнаруженных ошибок от вероятности ошибки для кодов (7,4) и (15,11).

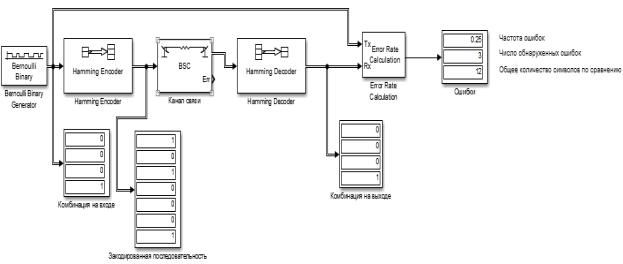
В рабочем поле необходимо собрать схему для работы кода Хэмминга (7,4). Схема представлена на рисунке 3.8.

Рис. 3.8. Линия передачи с применением кода Хэмминга

Всостав линии с кодированием входят:

1.BernoulliBinaryGenerator

2.HammingEncoder

3.Binary Symmetric Channel (каналпередачи)

4.HammingDecoder

5.Error RateCalculation (анализаторошибок)

133

6. Display

Устанавливаем характеристики блоков для кода (7,4)

Рис. 3.9. Параметры Bernoulli Binary Generator

Рис. 3.10. Параметры Hamming Encoder

Рис. 3.11. Параметры Binary Symmetric Channel

134

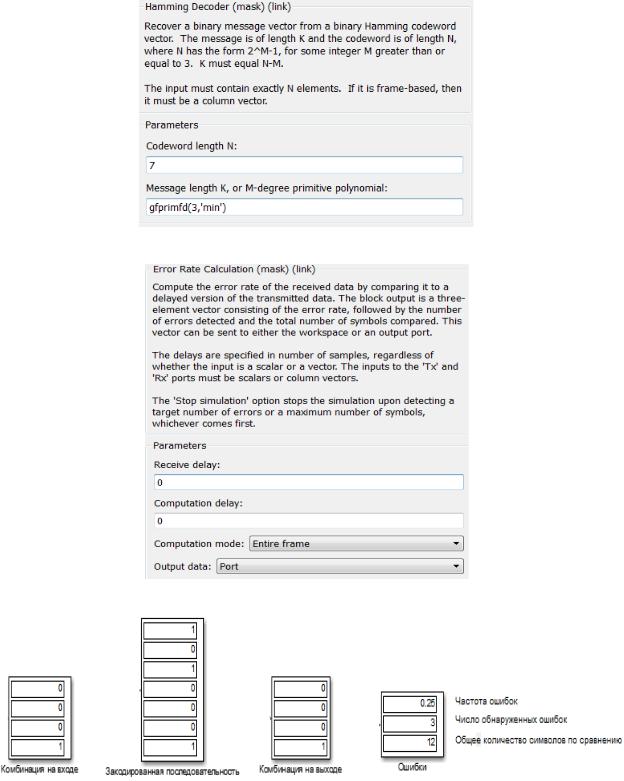
Рис. 3.12. Параметры Hamming Decoder

Рис. 3.13 Параметры Error Rate Calculation

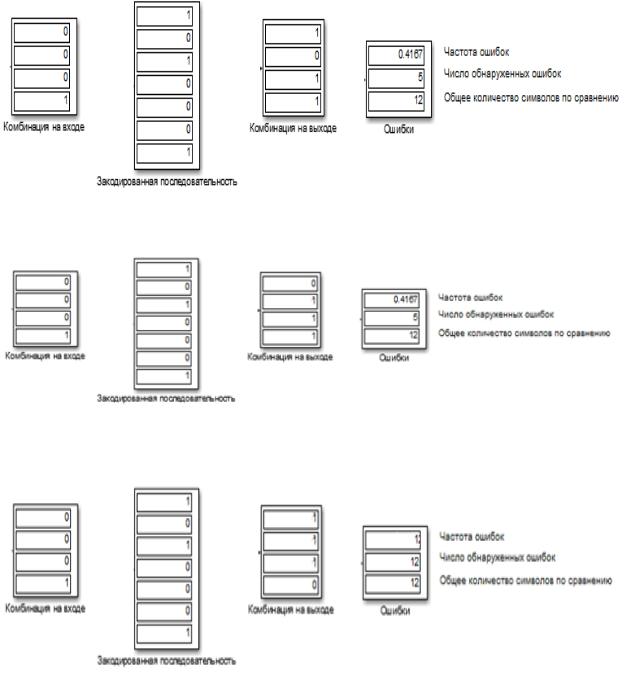
Рис. 3.14. Комбинация на входе, Закодированная последовательность, Комбинация на выходе, Ошибки (вероятность ошибок равна 0,2)

135

Анализируя рисунок выше, можно сделать вывод, что комбинация на входе совпадает с комбинацией на выходе, таким образом, передача осуществилась удачно. Что качается ошибок, то их частота равна 0,25, число обнаруженных ошибок равно 3, общее количество символов по сравнению равно 12. Кодирование и декодирование здесь осуществляется методом описанном в выше.

Рис. 3.15. Комбинация на входе, Закодированная последовательность, Комбинация на выходе, Ошибки (вероятность ошибок равна 0,4)

Рис. 3.16. Комбинация на входе, Закодированная последовательность, Комбинация на выходе, ошибки (вероятность ошибок равна 0,6)

Рис. 3.17. Комбинация на входе, Закодированная последовательность, Комбинация на выходе, Ошибки (вероятность ошибок равна 0,8)

Устанавливаем характеристики блоков для кода (15,11)

Рис. 3.19. Комбинация на входе, Закодированная последовательность, Комбинация на выходе, Ошибки (вероятность ошибок равна 0,2)

137

Рис. 3.20. Комбинация на входе, Закодированная последовательность, Комбинация на выходе, Ошибки (вероятность ошибок равна 0,4)

Рис. 3.21. Комбинация на входе, Закодированная последовательность, Комбинация на выходе, Ошибки (вероятность ошибок равна 0,6)

138

139

В результате проверки построена схема линии передачи с кодированием Хэмминга в среде Simulink. Построены графики зависимостей числа ошибок на выходе декодера от вероятности ошибки в канале связи для кодов (7,4) и (15,11).

Из графиков (рисунок 3.18 и рисунок 3.23) видно, что число ошибок увеличивается с ростом вероятности ошибок.

Код БЧХ (Боуза-Чоудхури-Хоквенгема)

Код БЧХ является циклическим кодом. С циклическим кодом Хэмминга у них много чего общего, а именно алгоритм кодирования, который отличается только

Кодирование:

Например, нужно построить БЧХ-код с длиной кодовых слов n=15и минимальным

расстоянием между кодовыми словами d=5. Степень примитивного многочлена равна

Декодирование:

Декодирование производится путем деления закодированной последовательности на генераторный полином, который использовался при кодировании. Полученная последовательность при делении и будет декодированной последовательностью. В лучшем случае, остатка при делении не будет, это значит, что ошибок не выявлено.

Если же остаток есть, называется он не иначе как синдром, в таком случае ошибки присутствуют в закодированной последовательности. В этом случае поступают так.

Закодированную последовательность складывают с вектором ошибок по модулю два, и

исправляют ошибочный бит. Вектор ошибок формируется с помощью специальных схем,

которые анализируя закодированную последовательность, формируют данный вектор.

Еще одним способ исправления ошибок является следующий метод. На основании полученного генераторного полинома строится схема и на каждом такте ее работы определяется синдром. В данном случае необходимо получить два синдрома, один из них это остаток, от деления полученный при декодировании, а второй это комбинация 100. Далее производится вычитание номера такта комбинации 100 и номера такта остатка. Полученная разность и является номером бита в закодированной комбинации.

Проведение эксперимента и обработка результатов

Задание:

1.Собрать схему

2.Подготовить схемы для реализации кодов БЧХ (15,7) и (15,11) основываясь на примере, представленном в отчете.

3.Для полученных кодов изменять вероятность ошибки в пределах от 0 до 1 (не менее 4-х точек) и снимать с дисплеев полученные входные последовательности,

закодированные последовательности, декодированные последовательности и ошибки.

4.Построить графики зависимости числа обнаруженных ошибок от вероятности ошибки для кодов (15,7) и (15,11).

5.Все поэтапное исследование представить в отчете.