
Теоретическая механика.-4
.pdf
В этом примере k = 0.56. Скорость в начале удара
составит v 
 2gH 7.7 м/с, а скорость отскока u = kv = 4.3 м/с.
2gH 7.7 м/с, а скорость отскока u = kv = 4.3 м/с.
Ударный импульс составит S = mv(1 + k) = 12 Hс. Средняя величина ударной силы будет S/ = 24 000 H.
2. Случай косого удара
Пусть вектор скорости v при падении тела на преграду составляет с нормалью к ней угол , а после отскока вектор скорости u – угол (рис. 4.23). Проектируем уравнение (4.29) на нормаль к преграде и на касательную к ней. Получим
n |
S |
u |
v |
Рис. 4.23
M (un – vn) = S, |
M (u – v ) = 0. |
(4.31)
Поскольку удар происходит только по направлению нормали к поверхности (если мы пренебрегаем трением),
коэффициент восстановления относится лишь к нормальным составляющим скоростей падения и отскока, т.е. k = – un / vn. Из
(4.31) получаем тогда
u = v , un = – k vn, S = M vn (1 + k).
Из этих соотношений можно найти модуль и направление скорости в конце удара и ударный импульс при известных M, v, k,
. В частности, из первого равенства с учетом того, что
un tg = vn tg ,
получим
tg / tg = k < 1.
Это означает, что при косом ударе угол падения (он отсчитывается от нормали к преграде) всегда меньше угла отражения.
4.9.5 Прямой центральный удар двух тел (шаров)
Удар двух тел называется прямым и центральным, если общая нормаль к поверхностям тел в точке касания проходит через их центры масс и скорости тел в начале удара направлены вдоль этой нормали. Примером такого удара является удар двух однородных шаров, центры которых до удара движутся вдоль одной и той же прямой (рис. 4.24).
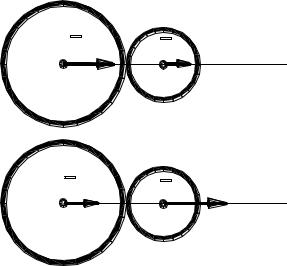
v1 |
v2 |
|
C1 |
C2 |
X |
u1 |
u2 |
|
C1 |
C2 |
X |
Рис. 4.24
Пусть имеем два тела с массами М1 и М2, скорости центров масс в начале удара v1, v2, в конце удара u1, u2 .
Направим ось С1х от центра первого шара через центр второго.
Для удара необходимо, чтобы первое тело догнало второе, или v1x
> v2x. Кроме того, после удара первое тело не может обогнать второе, и необходимо u1x < u2x .
Пусть при заданных массах, начальных скоростях и коэффициенте восстановления k происходит удар. Найдем скорости тел после удара.

Из системы уравнений (4.32), (4.33) можно найти скорости. Величина ударного импульса, например, для первого тела будет S1x = M1(u1x – v1x), а для второго S2x = – S1x .
Рассмотрим предельные случаи.
1. Абсолютно неупругий удар
В этом случае k = 0. Из (4.32), (4.33) находим
u1x u2x M1v1x M 2v2x . M1 M 2
(4.34)
После удара оба тела имеют одинаковые скорости.
Действующий на тела ударный импульс определяется как
S |
2x |
S |
|
M1M 2 |
(v |
v |
). |
|
|||||||
|
1x |
|
|
1x |
2x |
|
|
|
|
|
|
M1 M 2 |
|
|
|

2. Абсолютно упругий удар
В этом случае k = 1, и из (4.32), (4.33) получим
u1x |
v1x |
|
|
|
2M 2 |
|
|
(v1x v2 x ), |
|
|
M1 |
M |
2 |
|
|||||
|
|
|
|
|
|
||||
u2 x |
v2 x |
|
|
2M1 |
|
|
(v1x v2 x ). |
||
|
M1 |
M |
2 |
|
|||||
|
|
|
|
|
|
|
|||
Ударный импульс
S2x S1x 2M1M 2 (v1x v2x ).
M1 M 2
Таким образом, при абсолютно упругом ударе ударный импульс ровно вдвое больше, чем при абсолютно неупругом ударе.
В частном случае при равных массах M1 = M2 из полученных соотношений следует, что
u1x = v2x, u2x = v1x .
Отсюда видно, что при абсолютно упругом ударе два тела одинаковой массы обмениваются скоростями. Так, при прямом центральном ударе ударяющий бильярдный шар останавливается, а ударяемый неподвижный шар начинает двигаться со скоростью ударяющего.
4.9.6 Потеря кинетической энергии при неупругом ударе двух тел.
Теорема Карно
При неупругом ударе происходит потеря кинетической энергии соударяющихся тел. Наибольшая потеря будет при абсолютно неупругом ударе. Получим ее оценку для такого случая.
Запишем кинетическую энергию в начале и конце
удара:
2T M v2 |
M v2 |
, |
2T (M |
M |
) u2. |
(4.35) |
0 1 1x |
2 2x |
|
1 1 |
2 |
x |
|
Представим разность значений кинетической энергии в виде
T0 – T1 = T0 – 2T1 + T1. |
(4.36) |
Из уравнения (4.34) следует, что
(M1 + M2)ux = M1v1x + M2v2x,
и тогда
2T1 (M1 M 2 )ux2 (M1v1x M 2v2 x )ux ,
и из уравнения (4.36) с учетом уравнения (4.35) получим

T0 T1 12 M1v12x M 2 v22x 2M1v1x ux 2M 2 v2 x ux M1ux2 M 2ux2 ,
или
T0 T1 12 M1 (v1x ux )2 12 M 2 (v2 x ux )2 .
Разности в скобках – это не что иное, как изменение скорости каждого из соударяющихся тел. Их можно назвать потерянными при ударе скоростями. Из полученного выражения следует теорема Карно:
кинетическая энергия, потерянная системой при абсолютно неупругом ударе, равна той кинетической энергии,
которую имела бы система, если бы ее тела двигались с потерянными скоростями.
Проделав схожие выкладки при k 0, получим
