
Теоретическая механика.-4
.pdf
Функции, аналогичные введенной выше функции Лагранжа, описывают состояние других физических систем – непрерывной среды, электромагнитного поля и т.д., поэтому они играют важную роль в ряде разделов физики.
4.8.5 Примеры решения задач
Уравнениями Лагранжа можно пользоваться для изучения движения любой механической системы с геометрическими (или сводящимися к геометрическим) связями, независимо от числа тел и от того, какое движение (абсолютное или относительное) рассматривается.
Порядок составления уравнений Лагранжа:
1.Устанавливается число степеней свободы системы и выбираются обобщенные координаты.
2.Изображается система в произвольном положении, и на рисунке показываются все действующие на систему силы; для систем с идеальными связями показываются только активные силы.
3.Вычисляются обобщенные силы. Чтобы не ошибиться в знаках, каждое возможное перемещение системы направляется так, чтобы приращение соответствующей координаты было положительным.
4.Определяется кинетическая энергия системы в ее абсолютном движении и выражается через обобщенные координаты и обобщенные скорости.
5.Определяются частные производные от кинетической энергии по обобщенным скоростям и координатам и подставляются в уравнения (4.23).
Таким путем уравнения Лагранжа составляются независимо от того, рассматривается абсолютное или относительное движение. Но в последнем случае можно использовать и другой путь: кинетическую энергию системы рассматривать в ее относительном движении, но при нахождении обобщенных сил к силам, действующим на систему, присоединить переносные силы инерции.
|
|
|
|
|
d |
|
T |
|
T |
Q1. |
||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
dt |
|||||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
(4.25) |
|
Поскольку кинетическая энергия от угла не зависит, то |
|||||||||||
T |
0, и тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
d |
T |
|
|
|
||||
|
|
J0 |
, |
|
|
|
|
J0 . |
||||
|
|
|
|
|||||||||
|
|
|
dt |
|
|
|
|
|||||
Подставляя полученные значения в уравнение (4.25), получим
J0 Pa sin .
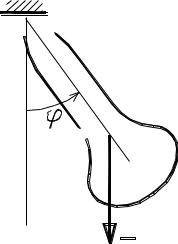
Если использовать то обстоятельство, что сила тяжести потенциальна, то уравнение Лагранжа можно составить в виде (4.24). Считаем ось Oz направленной вертикально вниз. Тогда
П = –Pz = – Pacos .
Следовательно |
|
|
|
|
|
L J 2 |
/ 2 Pa cos; |
L |
J , |
L |
Pa sin , |
|
|
||||
0 |
|
|
0 |
|
|
|
|
|
|||
и в результате решение уравнения в виде (4.24) дает такой же результат J0 Pa sin , что и в предыдущем случае.
Пример 2
Трубка ОА вращается в горизонтальной плоскости (совпадающей на рис. 4.21 с плоскостью чертежа) с постоянной угловой скоростью . Вдоль трубки движется шарик с массой m. В начальный момент времени он находится на расстоянии х0 от оси вращения, и скорость его равна нулю.
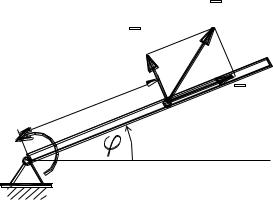

заданному закону движения трубки определяем приложенный к ней момент.
Пример 3
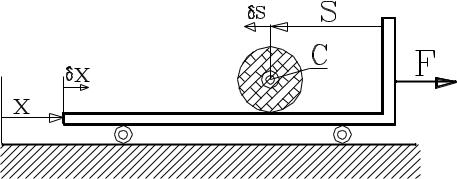
Тележка массой m1 под действием силы F движется горизонтально (рис. 4.22). На тележке находится сплошной цилиндрический каток массой m2. Каток может катиться по тележке без скольжения.
Определить ускорение тележки.
Рис. 4.22
Система имеет две степени свободы, так как ее состояние описывается положением тележки и положением катка на ней. В качестве обобщенных координат соответственно принимаем координату х тележки и координату s центра катка С относительно тележки. Тогда уравнения Лагранжа для системы будут:
d T |
|
|
T |
Q1, |
d |
T |
|
T |
Q2. |
|
|||
|
|
x |
|
x |
|
|
|
s |
(4.28) |
||||
|
|
||||||||||||
dt |
|
|
|
dt |
s |
|
|
|
|||||
Кинетическая энергия тележки и катка соответственно
|
|
2 |
|
|
2 |
|
|
2 |
|
T |
m1 x |
|
, |
T |
m2 vC |
J |
|
, |
|
|
|
|
C 2 |
||||||
1 |
2 |
|
|
2 |
2 |
|
|
||
где vC – абсолютная скорость катка, причем численно
vC x s.
Для сплошного цилиндра момент инерции определяется как JC = =m2r2/2, а при качении без скольжения
где в числителе – скорость центра С относительно тележки (а не абсолютная скорость). Итак:
T T1 |
T2 |
|
m x 2 |
|
m (x s)2 |
m s |
2 |
|
|
|
|||||||
|
1 |
|
2 |
|
|
|
2 |
, |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
4 |
|
|
|
, |
T m x m (x s), |
|
T m (s x) m2 s |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
1 |
|
|
|
2 |
|
|
|
|
s |
2 |
|
2 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
T |
T |
0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
x |
s |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для определения обобщенных сил придадим системе возможное перемещение, при котором координата х получит положительное приращение х. На этом перемещении работу совершает сила F, и величина этой работы определится равенством A1 = F x. На перемещении s активные силы работу не совершают, т.е. А2 = 0. Из этих равенств следует, что
Q1 = F, Q2 = 0.
Подставляем теперь полученные значения в (4.28) и находим дифференциальные уравнения движения системы
(m1 m2 )x m2s F, 3s 2x 0.
Выражаем из второго уравнения s 2x / 3 и, подставляя в первое уравнение, получаем искомое значение ускорения тележки
a1 x 3F /(3m1 m2 ).







 C
C



 K
K
 x
x