Теоретическая механика.-4

4.8.2 Обобщенные силы

Пусть на систему n материальных точек действуют силы F1, F2, … , Fn. Сама система имеет s степеней свободы, и ее положение описывается соответствующим числом обобщенных координат. Пусть мы сообщаем системе такое возможное перемещение, при котором координата q1 получит приращениеq1, а остальные координаты не меняются. Тогда каждый из радиусов-векторов системы получит элементарное приращение

Такое обозначение вводится для элементарного приращения соответствующего радиуса-вектора с номером k только при изменении q1 на q1. Сам радиус-вектор зависит от

всех обобщенных координат, поэтому ( rk )1 можно получить как частный дифференциал, т.е.

( rk )1 rk q1.

q1

Сумму работ всех действующих сил на рассматриваемом

перемещении обозначим индексом 1:

A1 F1 ( r1)1 F2 ( r2 )1 ... Fn ( rn )1

Вынесем в последней строчке этого выражения общий множитель q1 за скобки и получим

А1 = Q1 q1,

(*)

где введено обозначение

Q1 Fk rk .

q1

По аналогии с обычным выражением для работы величину Q1 называем далее обобщенной силой, отвечающей обобщенной координате q1. Очевидно, сообщая системе другое аналогичное перемещение, при котором меняется только вторая обобщенная координата, после повторения всех выкладок получим выражение для обобщенной силы, отвечающей второй

Если системе сообщить перемещение, при котором меняются все обобщенные координаты, то сумма элементарных работ будет

Ak = Q1 q1 + Q2 q2 +…+ Qs qs. (4.17)

Эта формула дает выражение полной элементарной работы всех действующих на систему сил в обобщенных координатах.

Из нее видно, что обобщенные силы – это величины

(коэффициенты) при приращениях обобщенных координат в выражении полной элементарной работы действующих на систему сил.

Если связи в системе идеальные, то работа их реакций равна нулю, и работу совершают только активные силы. В этом случае величины Qk представляют собой обобщенные активные силы системы.

Размерность обобщенной силы зависит от размерности соответствующей обобщенной координаты.

Размерность обобщенной силы равна размерности работы, деленной на размерность соответствующей обобщенной координаты:

[Q] = [A]/[q].

Таким образом, обобщенная сила совпадает по размерности с обычной лишь в случае, когда обобщенная координата имеет смысл линейной величины (расстояния).

Вычисление обобщенных сил проводим в соответствии с полученными выше выражениями через возможную элементарную работу. При этом сначала устанавливается число степеней свободы системы, выбираются обобщенные координаты, а на чертеже изображаются все приложенные к системе активные силы и силы трения (если они совершают работу). Для определения первой обобщенной силы Q1 нужно сообщить системе такое перемещение, при котором координата q1 получает положительное приращение q1, и вычислить на этом перемещении сумму элементарных работ всех сил. Коэффициент при q1 в выражении (*) и даст искомое значение обобщенной силы Q1. Аналогично можно вычислить все остальные обобщенные силы.

Пример 1

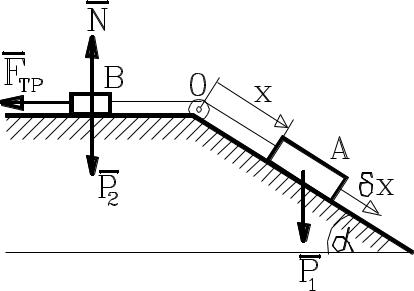
Груз Р1 перемещается по гладкой наклонной плоскости, а груз Р2 – по горизонтальной поверхности с коэффициентом трения f (рис. 4.18). Грузы связаны нитью, трением в блоке и

массой нити пренебречь. Определить обобщенную силу для этой системы.

Рис. 4.18

Эта система имеет одну степень свободы. Положение системы полностью определяется координатой q1 = х, положительное направление которой показано на рисунке. Сообщаем системе возможное перемещение х, при котором оно

тоже положительно, и вычисляем элементарную работу сил P1 и

трения FTP . Остальные силы работу не совершают. Так как FTP = fN= fP2, то

А = (P1 sin – f P2 ) x.

Отсюда обобщенная сила, как было сказано ранее, - это

множитель перед x, т.е.

Q1 = P1 sin – f P.

Пример 2

Однородный стержень длиной l и весом р может вращаться в вертикальной плоскости (в плоскости чертежа) вокруг оси А (рис. 4.19). На стержне нанизан шарик весом Р, который удерживается в равновесии пружиной. Длина пружины в ненапряженном состоянии равна b0, а ее жесткость определяется величиной с. Найти для этой системы обобщенные силы.

Система имеет две степени свободы: ее положение полностью определено, если известны угол поворота стержня вокруг оси и положение шарика на стержне. Принимаем в качестве обобщенных координат угол и расстояние х шарика от конца ненапряженной пружины (q1 = , q2 = x).

Сообщим системе сначала возможное перемещение, когда меняется только первая обобщенная координата, угол , на величину > 0. При этом x = const. На этом перемещении

работу совершают силы p и P . Находим соответствующую работу с учетом того, что направление момента противоположно направлению вращения:

A1 = [–(Pl/2) sin – p(b0 + x) sin ] ,

следовательно:

Q1 = – [Pl/2 + p(b0 + x)] sin .

Теперь сообщаем системе возможное перемещение, при котором меняется только вторая координата х на величину x > 0 при условии = const. На этом возможном перемещении

работу совершают сила тяжести p и сила упругости F , модуль которой F = cx. Тогда

A2 = (pcos – cx)x,

и

Q2 = pcos – cx.

Первая обобщенная сила имеет размерность момента (так как первая обобщенная координата имеет размерность угла), а вторая – размерность обычной силы.

Случай потенциальных сил

Если все силы, действующие на систему, являются потенциальными, то для системы существует силовая функция U, в общем случае зависящая от координат, такая, что сумма элементарных работ действующих сил равна полному дифференциалу этой функции, т.е. Ak = U. Но при переходе к обобщенным координатам q1, q2, … , qs все величины xk, yk, zk могут быть выражены через эти координаты. Тогда

U = U(q1, q2,…, qs).

Следовательно, вычисляя U как полный дифференциал от U, получим

Сравнивая это с выражением (4.17), заключаем

или, поскольку потенциальная энергия П = – U,

Таким образом, если все действующие на систему силы

являются потенциальными, то обобщенные силы равны частным производным от силовой функции (или взятым со знаком минус частным производным от потенциальной энергии системы) по соответствующим обобщенным координатам.

Пример 3

Рассмотрим еще раз систему, представленную на рисунке 4.19. Все силы в этой системе потенциальны. Если ввести ось Oz, направленную вертикально вверх, то потенциальная энергия всей системы получается в виде выражения:

П = –(Pl/2) cos – p(b0 + x) cos + cx2/2,

где обобщенными координатами по-прежнему служат q1 = , q2 = x. Тогда

что совпадает с результатами, полученными в примере 2.

4.8.3 Условия равновесия системы

вобобщенных координатах

Всоответствии с принципом возможных перемещений

необходимым и достаточным условием равновесия механической системы является равенство нулю суммы элементарных работ всех активных сил (и сил трения, если они совершают работу) на любом возможном перемещении системы, т.е.

Ak = 0.

В обобщенных координатах это записывается в виде

Q1 q1 + Q2 q2 +… + Qs qs = 0.

В этом соотношении q1, q2 ,…, qs между собой независимы, и равенство левой части нулю возможно лишь тогда, когда

Q1 = Q2 = … = Qs = 0.

(4.18)

Таким образом, для равновесия механической системы

необходимо и достаточно, чтобы все обобщенные силы, соответствующие выбранным для системы обобщенным координатам, были равны нулю. Число условий равновесия равно числу обобщенных координат или числу степеней свободы системы.

По существу, при решении задач в рассмотренных выше примерах (см., например, задачи с рис. 4.14, 4.15) мы с помощью принципа возможных перемещений вычисляли соответствующие обобщенные силы, а затем приравнивали их нулю.

В случае потенциальных сил условия равновесия (4.18) можно переписать в виде

или

Но это означает, что полный дифференциал U или П равен нулю:

Эти равенства представляют собой условия экстремума

функции нескольких переменных. Следовательно, система

находится в равновесии только тогда, когда ее потенциальная

энергия имеет экстремум.

4.8.4 Уравнения Лагранжа

Общее уравнение динамики можно записать в обобщенных координатах как уравнение статики, присоединив к активным силам еще и силы инерции:

Ak Aku 0.

(4.19)

В первую сумму здесь могут входить как работа активных сил, так и работа сил трения.

Пусть система имеет s степеней свободы. Тогда с использованием обобщенных координат

Ak = Q1q1 + Q2q2 +…+ Qsqs.

Преобразуем к обобщенным координатам и элементарную работу сил инерции. Делаем это по аналогии с выражением для работы активных сил. Тогда получим

Aku Q1uq1 Q2uq2 ... Qsuqs ,

где введены так называемые обобщенные силы инерции, которые

можно представить по аналогии с активными силами в виде

Подставляя эти значения в выражение (4.19), получим

(Q1 Q1u ) q1 (Q2 Q2u ) q2 ... (Qs Qsu ) qs 0.

В силу независимости между собой q1 , q2 , ..., qs для выполнения этого равенства необходимо, чтобы

Полученными выражениями можно пользоваться для решения задач динамики. Однако получение уравнений движения упрощается, если выразить обобщенные силы инерции через кинетическую энергию системы.

Поскольку сила инерции любой точки системы определяется как

то в первом из выражений (4.20) будет

Преобразуем правую часть этого выражения так, чтобы она содержала только скорости точек системы. Заметим, что