Теоретическая механика.-4

перемещением этой точки. Возможную работу активной силы F a обозначим Aa F a r , а возможную работу реакции

связи N обозначим Ar N r.

Дадим общее определение идеальной связи: идеальными

связями называем такие, для которых сумма элементарных работ их реакций на любом возможном перемещении системы равна нулю, т.е.

Akr 0.

Так как при стационарных связях каждое действительное перемещение совпадает с одним из возможных, это определение совпадает с ранее введенным определением в п.

4.5.2.

Докажем, что если механическая система с идеальными связями находится под действием приложенных сил в равновесии, то при любом возможном перемещении системы должно выполняться равенство

где k – угол между силой и возможным перемещением. Обозначим равнодействующие всех (внешних и

внутренних) активных сил и реакций связей, действующих на точку с номером k, соответственно через Fka , Nk . Поскольку каждая точка системы находится в равновесии, то

Fka Nk 0.

Работа этой нулевой суммы сил на любом перемещении точки равна нулю, но тогда после суммирования получим

Aka Akr 0.

Поскольку связи идеальные, а перемещения точек являются возможными, то вторая сумма в полученном равенстве равна нулю. Тогда равна нулю и первая сумма. Этим доказывается, что равенство (а) выражает условие равновесия системы.

Можно показать, что это условие является не только необходимым, но и достаточным условием равновесия.

Таким образом, доказан принцип возможных перемещений:

для равновесия механической системы с идеальными связями

необходимо и достаточно, чтобы сумма элементарных работ всех действующих на нее активных сил при любом возможном перемещении системы была равна нулю.

Пример 1

Найти зависимость между силами P и Q в механизме, показанном на рис. 4.14, при равновесии.

Q A SA B

P

SB

Рис. 4.14

У этой системы одна степень свободы. Придадим системе возможное горизонтальное перемещение, тогда каждая горизонтальная диагональ ромба, образованного стержнями, удлинится на одну и ту же величину S. В итоге смещение точки В составит SB = 3 S, а смещение точки А будет SА = S. Используем условие равновесия (а), в нашем случае оно принимает вид

P SB - Q SА = 0, или (3P-Q) S = 0,

откуда Q = 3P.

Пример 2

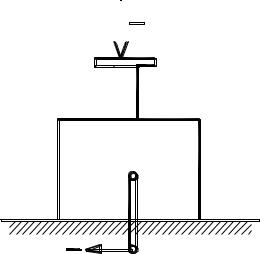
Найти зависимость между силами P, Q в подъемном механизме, детали которого неизвестны, если при каждом полном обороте рукоятки AB длиной b винт D выдвигается на величину h (рис. 4.15).

Q

D

Возможное перемещение точки А приложения силы определяется величиной b , где характеризует поворот рукоятки. Возможное перемещение винта D обозначим S. Условие равновесия (а) приводит к равенству

Если считаем, что при вращении рукоятки АВ винт D выдвигается равномерно, то

/2 = S/h.

В ы ра жая от с ю д а и подставляя в условие равновесия (*), получаем

Q= 2 bP/h.

За м ет им , чт о р еш ен и е п ол уч ен о п р и от с ут с т в и и ка к ой - л и б о и н ф ор м а ц и и о ст р оен и и м ех а н из м а , и д р уг и м и м ет од ам и –

н а п р и м ер , м ет од а м и г ео м ет р и ч ес к ой ст ат ик и – ег о п олуч и т ь н ев оз м ож н о .

4.7.4 Общее уравнение динамики

Принцип возможных перемещений дает общий метод решения задач статики. С другой стороны, принцип Даламбера позволяет использовать методы статики для решения задач динамики. Таким образом, объединяя и используя эти два

принципа одновременно, получаем общий метод решения задач динамики.

Итак, пусть имеется система материальных точек, на которую наложены идеальные связи. Ко всем точкам системы, кроме действующих на них активных сил и реакций связей, добавим еще и силы инерции. Тогда, в соответствии с принципом Даламбера, система сил будет находиться в равновесии. Применим теперь принцип возможных перемещений:

Aka Aku Akr 0.

Первое слагаемое – работа активных силы, второе – сил инерции, третье – реакций связей. Но последняя сумма по определению идеальных связей равна нулю. Тогда

Aka Aku 0.

(4.13)

Это равенство выражает собой принцип ДаламбераЛагранжа:

при движении механической системы с идеальными связями в каждый момент времени сумма элементарных работ всех приложенных активных сил и всех сил инерции на любом возможном перемещении системы будет равна нулю.

Уравнение (4.13) называется общим уравнением динамики.

В аналитической форме оно может быть записано в

виде

(Fkxa Fkxu ) xk (Fkya Fkyu ) yk (Fkza Fkzu ) zk 0.

(4.14)

Уравнения (4.13) или (4.14) позволяют составить уравнения движения механической системы. Если система представляет собой совокупность твердых тел, нужно к действующим на каждое тело активным силам прибавить приложенную в любом

центре силу, равную главному вектору сил инерции, и пару с моментом, равным главному моменту сил инерции относительно этого центра, а затем применить принцип возможных перемещений.

Пример

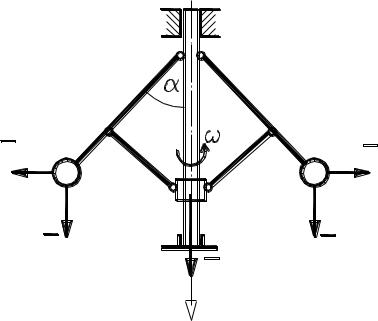
Пусть центробежный регулятор равномерно вращается с угловой скоростью (рис. 4.16). Вес каждого из шаров р, а вес муфты равен Q3 . Пренебрегая весом стержней, найти угол ,

если OD1 = OD2 = l, OB1 = OB2 = B1C1 = B2C2 = b.

Рис. 4.16

Активные силы в данном примере – силы тяжести p, Q3. Присоединяем к ним еще силы инерции шаров (для муфты этой силой пренебрегаем – она много меньше, чем силы инерции шаров). Составим общее уравнение динамики в форме (4.14):

Далее учитываем, что

Q3 = Q, p1 = p2 = p, F1u F2u ( p / g)aD ( p / g) 2l sin .

Координаты точек приложения сил

x1 = х2 = lcos , y2 = – y1 = lsin , x3 = 2bcos .

Дифференцируя эти выражения, находим

x 1 = x2 = – lsin ,y2 = – y1 = lcos ,x3 = 2bsin .

Подставляя все эти выражения в уравнение работ (*), получаем

[–2plsin + 2(p/g)l2 2 sin cos – 2Qbsin ] = 0.

Отсюда окончательно

отклоняться, если

2 ( pl Qb)g / pl 2 .

Сувеличением угловой скорости cos в соответствии

с(4.15) будет стремиться к нулю, а сам угол – к величине прямого угла.

4.8 Условия равновесия и движения системы в обобщенных координатах

4.8.1 Обобщенные координаты и обобщенные скорости

Ранее было установлено, что для системы с голономными (геометрическими) связями число независимых координат, определяющих ее положение, совпадает с числом ее степеней свободы. В качестве таких координат можно выбирать параметры, имеющие любую размерность и любой геометрический или механический смысл. Так, координатами могут служить отрезки прямых, дуг, углы, площади и т.д.

Независимые между собой параметры любой размерности, число которых равно числу степеней свободы системы и которые однозначно определяют ее положение, называют обобщенными координатами системы. Далее для обозначения этих координат используем букву q. Положение системы с s степенями свободы будет определяться, таким образом, обобщенными координатами

q1, q2, …, qs.

Поскольку обобщенные координаты между собой независимы, то элементарные приращения этих координат

q1, q2, …, qs

(4.16)

тоже независимы между собой. При этом каждая из величин

(4.16) определяет соответствующее возможное перемещение

системы, независимое от других.

Известно, что всегда можно перейти от одной системы

координат к другой, с таким же числом независимых координат.

Так, декартовы координаты xk, yk, zk любой точки системы можно

выразить через обобщенные координаты зависимостями вида

хk = xk(q1, q2, …, qs),

yk = yk(q1 ,q2, …, qs),

zk = zk(q1, q2, …, qs).

Следовательно, для радиуса-вектора этой точки тоже можно записать выражение

rk rk (q1 , q2 ,..., qs ).

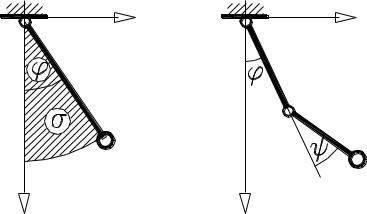
Пример 1

Плоский математический маятник ОМ имеет одну степень свободы, так как для описания его положения достаточно одной координаты (рис. 4.17, а). В качестве такой обобщенной координаты можно выбрать или угол , или длину дуги s, отсчитываемую от положения равновесия, или площадь сектора. В любом случае необходимо только указать положительное и отрицательное направления отсчета этих координат. Неудачным следует признать выбор в качестве обобщенной координаты расстояния вверх от положения равновесия, так как одному значению координаты могут отвечать два положения маятника – слева и справа от положения равновесия.

При движении системы меняется ее положение и соответственно значения обобщенных координат, что можно записать в виде

q1 = f1(t), q2 = f2(t),…, qs = fs(t).

Эти уравнения называются кинематическими уравнениями движения системы в обобщенных координатах.

Производные по времени от обобщенных координат называются обобщенными скоростями системы. Обозначаются эти производные как обычно – точкой над соответствующим символом или как dqk/dt. Размерность обобщенной скорости зависит от того, какая величина принята в качестве обобщенной координаты. Так, если координата линейная величина, то обобщенная скорость имеет размерность обычной линейной скорости. Если координата – угол, то обобщенная скорость имеет размерность угловой скорости, если в качестве координаты берется площадь сектора, то соответствующая скорость – секторная скорость и т.д.