ПРИМЕРЫ СОДЕРЖАТЕЛЬНЫХ ЗАДАЧ И РЕШЕНИЙ

Примеры 2.1. Закон распределения дискретной случайной величины

Примеры 2.2. Закон распределения непрерывной случайной величины. Плотность распределения. Математическое ожидание, дисперсия

Примеры 2.3. Свойства нормального распределения

Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Томский Государственный Университет Систем Управления и Радиоэлектроники

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Теория вероятностей и математическая статистика.-2.pdf

Скачиваний:

Добавлен:

05.02.2023

Размер:

469.85 Кб

Скачать

☆

<<< < Предыдущая 1 2 34 / 104 5 6 7 8 9 10 > Следующая >>>

2.Задана плотность распределения вероятностей

0, x 1


f (x) ax2 b, -1 x 1
	1,	x 1

Найти: а) константы а; b б) функцию распределения F(x), в ответ ввести значения F(– 1/3), F(1/3); в) М(Х); г) D(X); д) Р(–1/2 < X < 0.7).

3. Изделие считается пригодным, если отклонение его размера от номинала не превышает по модулю 0.45 мм. Случайные отклонения X распределены нормально, причём М(Х)=0, (Х)=0.5 мм. Определить вероятность того, что случайно взятое изделие является пригодным.

1. Найти закон распределения дискретной случайной величины X – числа появлений «орла» при двух бросаниях монеты.

Решение. Возможные значения случайной величины: 0, 1, 2. Вероятности этих значений находим по формуле Бернулли:

P X 0 P2 (0) C20 p0q2

0.50

0.52

0.25;

0!2!

P X 1 P2 (1) C21 p1q1

0.51 0.51 0.50;

1!1!

P X 2 P2 (2) C22 p2q0

0.52

0.50

0.25.

2!0!

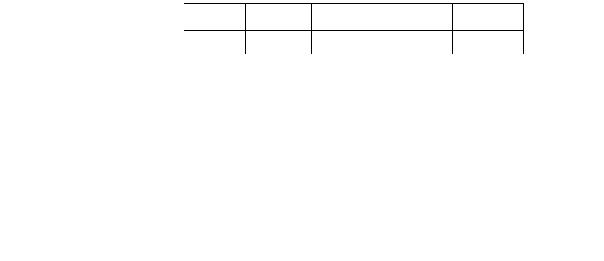
Записываем ряд распределения:

Таблица 2.1 Ряд распределения

0.25

0.50

0.25

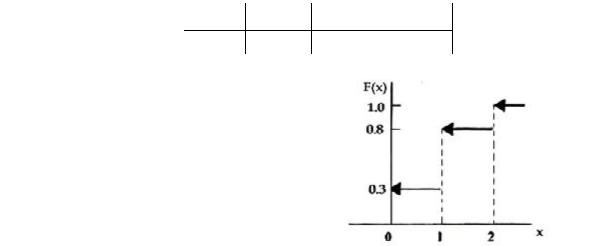
Записываем функцию распределения и строим ее график:

	0,

0.3,
F x
0.8,
	1,
	1,

x 0;

0<x 0;

1<x 2;

x 2

Рисунок 2.1. Формула и график функции распределения

2. Найти математическое ожидание дискретной случайной величины, заданной рядом распределения:

Таблица 2.2 Ряд распределения

X	0	1	2	3
p	0.2	0.4	0.3	0.1
Решение.
4
M X = pi xi .=0 0 . 2	+ 1 0 . 4 + 2 0.3		+ 3 0 . 1 =1.3.

i=1

3.Найти дисперсию случайной величины, заданной рядом распределения из 2. Решение. Чтобы вычислить дисперсию, необходимо знать математическое ожидание. Для данной случайной величины выше было найдено: m=1.3. Вычисляем дисперсию по формуле (3.5):

	4
D X M X 2 m2 xi2 pi		m2 .
	i 1
= 02 0.2	12 0.4 22	0.3 32	0.11.32	0.81.

1. Случайная величина X задана плотностью распределения

a cos x,		- /2 x /2,
f x	0,	x <- /2,	x /2

Требуется:

а) найти значение коэффициента а; б) найти функцию распределения;

в) найти вероятность попадания случайной величины на интервал (0, /2 ). Решение, а) Воспользуемся свойством 3:

a cos x dx a sin x

f x dx

a 1 ( 1) 2a 1.

- /2

Отсюда получаем: а=1/2.

б) Если x /2 , то

F x f t dt 0 dt 0;

если - /2 x /2, то

- /2

F x

0 dt

cost dt

sin t

sin x 1 ;

- /2

если x /2 , то

- /2

F x

0 dt

cost dt

0 dt

sin t

- /2

Таким образом,

				0,					x <- /2,
	1
	1
F x			sin x 1 ,						- /2 x /2,
F x	2		sin x 1 ,						- /2 x /2,
	2			1,					x /2.
				1,					x /2.
в) По свойству 4:
в) По свойству 4:							1			1
P 0 X / 4 F / 4 F 0							1	sin / 4 1		1	sin 0 1
P 0 X / 4 F / 4 F 0							2	sin / 4 1		2	sin 0 1
1						1
1		2				1		2
					1				.
					1				.
2	2					2	4
2	2					2	4

2. Найти математическое ожидание случайной величины, заданной плотностью распределения:

	x / 2,						0 x 2,							.
f x					x <0,					x 2				.
	0,				x <0,					x 2
	2		1			2		2					x3		8
	2		1			2		2					x3		8
Решение. M X = xf x dx	x x / 2 dx					x			dx							1.33.
Решение. M X = xf x dx	x x / 2 dx					x			dx							1.33.
	0		2			0				6					6
	0		2			0				6					6
3. Случайная величина задана плотностью распределения
	1/ 2 cos x,									x		/ 2,
	1/ 2 cos x,									x		/ 2,

f x 0,										x
											/ 2.
											/ 2.


Найти дисперсию и среднее квадратическое отклонение.
Решение. Находим сначала математическое ожидание:
	xf x dx	1		/2
m=		1					x cos x dx 0
m=							x cos x dx 0
	2		/2

(как интеграл от нечетной функции по симметричному промежутку). Теперь вычисляем дисперсию и среднее квадратическое отклонение:

D X x m 2 f x dx

x2 cos x dx

cos x dx x2 sin x

x sin x dx

sin x

x cos x dx

2x cos x

sin x

2x cos x

2sin x

;

D X

Решение. Р(– 3 < X < 3) = Р( | X | < 3) =

= 0.7. Отсюда следует, что

2. Полезный справочный материал.

А. Если случайная величина N m, 2 ,

то

N 0,1 .

В. Если случайная величина N m, 2 , то

P x x

0,1

В частности, P

l 2 0,1

Таким образом, вычисление любых вероятностей для нормально распределённой случайной величины сводится к вычислению функции распределения 0,1 x . Она

обладает следующими свойствами: 0,1 0 0.5;	0,1 x 1 0,1 x .
С. Если N 0,1 , то для любого x 0

Px 1 20,1 x 20,1 x 1.

D.Правило трех сигм. Если N m, 2 , то

P m 3 0.0027.

Большого смысла в запоминании числа 0.0027 нет, но полезно помнить, что почти вся масса нормального распределения сосредоточена в границах от a 3 до a 3 .

2. Дана случайная величина X N 1,4 . Найти			P 2 X 3 .
Решение. По формуле свойства		В при	x1 2, x2 3,	m 1, 2	получаем
P 2	X 3 (1) (0.5). По	таблице	для функции Лапласа		находим
(0.5) 0.1915, (1) 0.3413.
P 2	X 3 0.3413 0.1915 0.1498.

3. Случайная величина X – отклонение размера изделия от нормы – нормально распределенная, причём М (Х)= 0. Найти (Х), если известно, что Р(– 3 < X < 3) = 0.7.

3 0.35 , и, используя табличные данные (приложение 1), получаем 3/ =1.4,

0,1

или = 3/1.4 2.14.

<<< < Предыдущая 1 2 34 / 104 5 6 7 8 9 10 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
05.02.2023760.21 Кб8Теория автоматического управления.-7.pdf
#
05.02.20231.36 Mб9Теория автоматического управления..pdf
#
05.02.2023770.68 Кб12Теория автоматов и формальных языков..pdf
#
05.02.2023314.52 Кб8Теория алгоритмов и математическая логика..pdf
#
05.02.2023725.19 Кб8Теория вероятностей и математическая статистика.-1.pdf
#
05.02.2023469.85 Кб7Теория вероятностей и математическая статистика.-2.pdf
#
05.02.2023722.49 Кб9Теория вероятностей и математическая статистика.-3.pdf
#
05.02.20231.59 Mб5Теория вероятностей и математическая статистика.-4.pdf
#
05.02.2023487.26 Кб8Теория вероятностей и математическая статистика.-5.pdf
#
05.02.20231.1 Mб16Теория вероятностей и математическая статистика.-6.pdf
#
05.02.20231.64 Mб9Теория вероятностей и математическая статистика.-7.pdf