Тестирование и диагностика в радиоэлектронных системах передачи информации

292

Рис. П1.52. Вероятности ошибок в системах QAM.

Достоинство высоких значений номера QAM – это повышенная скорость передачи данных, поскольку таким образом большее количество битов информации может быть передано в течении одного цикла. Однако, с другой стороны, в этом случае большее число уровней амплитуды сигнала располагаются близко друг к другу, повышая тем самым вероятность неразличимости двух уровней, и как следствие – повышая чувствительность системы к шуму. Таким образом, высокие значения номера QAM более требовательны к параметру SNR (Signal Noise Ratio – Отношение Сигнал/Шум).

Практическая часть QAM

Рис. П1.53. Внешний вид разработанного ПО для исследования QAM

293

Число посылок 2000 и различные отношения сигнал/шум

Рис. П1.54. Созвездия для QAM-8 передаваемого сигнала.

Рис. П1.55. Созвездия для QAM-16 передаваемого сигнала.

Рис. П1.56 Созвездия для QAM-32 передаваемого сигнала.

294

На рисунке П1.57. приведены глазковые диаграммы для QAM-8 сигнала.

Рис. П1.57. Глазковые диаграммы при малом отношении сигнал/шум и при наилучшем отношении сигнал/шум

На рисунке П1.58. приведены глазковые диаграммы для QAM-16 сигнала.

Рис. П1.59. Глазковые диаграммы при малом отношении сигнал/шум и при наилучшем отношении сигнал/шум

Рис. П1.60. Глазковые диаграммы при малом отношении сигнал/шум и при наилучшем отношении сигнал/шум

295

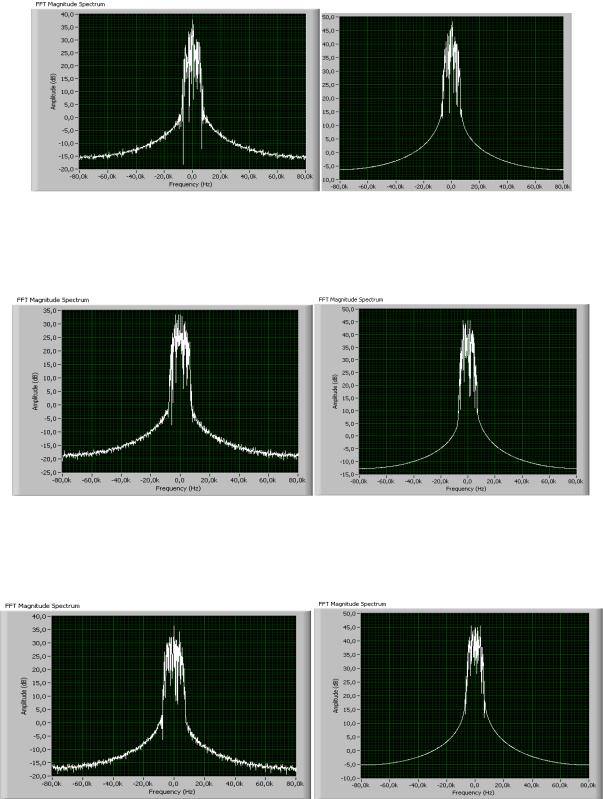
На рисунке П1.61 приведены спектрограммы для QAM-8 сигнала.

Рис. П1.61. Спектрограммы на входе и на выходе канала На рисунке П1.62. приведены спектрограммы для QAM-16 сигнала.

Рис. П1.62. Спектрограммы на входе и на выходе канала На рисунке П1.63 приведены спектрограммы для QAM-32 сигнала.

Рис. П1.63. Спектрограммы на входе и на выходе канала

296

Ползунком Eb/N0 устанавливается уровень отношения сигнал/шума, в поле BER

отображается количество обнаруженных ошибок при передаче. Из полученных данных можно построить график зависимости, сравнить показатели у различных видов модуляции и подтвердить/опровергнуть теорию, описанную выше.

В таблице ниже представлены данные для рассмотренных видов модуляций.

На рисунке представлен график зависимости параметра BER от Eb/N0 для 8-QAM, 16QAM, 32-QAM

Рис. П1.64. График зависимости параметра BER от Eb/Nо для 8-QAM, 16-QAM, 32-QAM

297

П.1.3 ТЕСТИРОВАНИЕ И ДИАГНОСТИКА КОДЕКОВ СИСТЕМ РАДИОСВЯЗИ

(Компьютерный практикум)

1. Циклические избыточные коды CRC (Cyclic redundancy check) [12]

Циклический избыточный код (CRC). Наиболее известными из методов

обнаружения ошибок передачи данных являются:

Посимвольный контроль чётности, называемый также поперечным, подразумевает передачу с каждым байтом дополнительного бита, принимающего единичное значение по чётному или нечётному количеству единичных бит в контролируемом байте. Посимвольный контроль чётности прост как в программной, так и в аппаратной реализации, но его вряд ли можно назвать эффективным методом обнаружения ошибок, так как искажение более одного бита исходной последовательности резко снижает вероятность обнаружения ошибки передачи. Этот вид контроля обычно реализуется аппаратно в устройствах связи.

Поблочный контроль чётности, называемый продольным. Схема данного контроля подразумевает, что для источника и приёмника информации заранее известно, какое число передаваемых символов будет рассматриваться ими как единый блок данных. В этой схеме контроля для каждой позиции разрядов в символах блока (поперёк блока) рассчитываются свои биты чётности, которые добавляются в виде обычного символа в конце блока. По сравнению с посимвольным контролем чётности, поблочный контроль чётности обладает большими возможностями по обнаружению и даже корректировке ошибок передачи, но всё равно ему не удаётся обнаруживать определённые типы ошибок.

Вычисление контрольных сумм. В отличие от предыдущих методов, для метода контрольных сумм нет чёткого определения алгоритма. Каждый разработчик трактует понятие контрольной суммы по-своему. В простейшем виде контрольная сумма – это арифметическая сумма двоичных значений контролируемого блока символов. Но этот метод обладает практически теми же недостатками, что и предыдущие, самый главный из которых

–нечувствительность контрольной суммы к чётному числу ошибок в одной колонке и самому порядку следования символов в блоке.

Контроль циклически избыточным кодом – CRC. Это гораздо более мощный и широко используемый метод обнаружения ошибок передачи информации. Он обеспечивает обнаружение ошибок с высокой вероятностью. Кроме того, этот метод обладает рядом других полезных моментов, которые могут найти своё воплощение в практических задачах.

Циклический избыточный код (англ. Cyclic redundancy code, CRC) – алгоритм

вычисления контрольной суммы, предназначенный для проверки целостности передаваемых

298

данных. Алгоритм CRC обнаруживает все одиночные ошибки, двойные ошибки и ошибки в нечётном числе бит. Понятие циклических кодов достаточно широкое, однако на практике его обычно используют для обозначения только одной разновидности, использующей циклический контроль (проверку) избыточности.

Главная особенность значения CRC состоит в том, что оно однозначно идентифицирует исходную битовую последовательность и поэтому используется в различных протоколах связи, а также для проверки целостности блоков данных, передаваемых различными устройствами. Благодаря относительной простоте алгоритм вычисления CRC часто реализуется на аппаратном уровне.

При передаче пакетов по сетевому каналу могут возникнуть искажения исходной информации вследствие разных внешних воздействий: электрических наводок, плохих погодных условий и многих других. Сущность методики в том, что при хороших характеристиках контрольной суммы в подавляющем числе случаев ошибка в сообщении приведёт к изменению его контрольной суммы. Если исходная и вычисленная суммы не равны между собой, принимается решение о недостоверности принятых данных, и можно запросить повторную передачу пакета.

Основная идея алгоритма CRC состоит в представлении сообщения в виде огромного двоичного числа, делении его на другое фиксированное двоичное число и использовании остатка этого деления в качестве контрольной суммы [12]. Получив сообщение, приёмник может выполнить аналогичное действие и сравнить полученный остаток с «контрольной суммой».

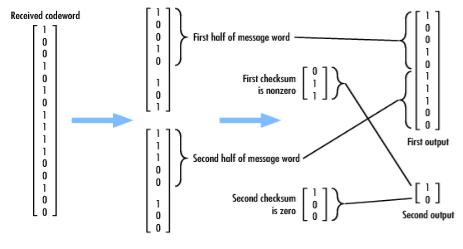
На рисунках П1.65 и П1.66 изображено графическое представление кодирования и декодирования CRC-кода:

Рис. П1.65. Принцип работы кодера CRC

299

Рис. П1.66. Принцип работы декодера CRC

Степенью CRC-полинома W называют позицию самого старшего единичного бита.

Например, степень полинома 100112 равна 4.

Для вычисления CRC используют полиномиальную арифметику. Вместо представления делителя, делимого (сообщения), частного и остатка в виде положительных целых чисел,

можно представить их в виде полиномов с двоичными коэффициентами или в виде строки

упрощённо: x4 x2 x1 1.

И сообщение, и делитель могут быть представлены в виде полиномов, с которыми можно выполнять любые арифметические действия без переносов.

Как правило, контрольная сумма добавляется к исходному сообщению и полученное расширенное сообщение передаётся через канал связи.

На другом конце канала приёмник может сделать одно из возможных действий (оба варианта совершенно равноправны):

1.Выделить текст полученного сообщения, вычислить для него контрольную сумму и сравнить её с переданной.

2.Вычислить контрольную сумму для всего переданного сообщения, и посмотреть,

получится ли в результате нулевой остаток.

Поскольку исходное сообщение может быть очень большим (до нескольких Мбайтов) и

так же из-за того, что для получения CRC используется CRC-арифметика, использовать обычную компьютерную операцию деления нельзя.

Самый популярный и рекомендуемый IEEE полином для CRC-32 используется в

Ethernet, FDDI; также этот многочлен является генератором кода Хемминга. Использование

300

другого полинома — CRC-32C — позволяет достичь такой же производительности при длине исходного сообщения от 58 бит до 131 кбит, а в некоторых диапазонах длины входного сообщения может быть даже выше — поэтому в наши дни он тоже пользуется популярностью. К примеру, стандарт ITU-T использует CRC-32C с целью обнаружения ошибок в полезной нагрузке.

Ниже в таблице перечислены наиболее распространённые многочлены — генераторы

CRC: