y |
|
|
|
|
graff-1 |
|
|
|
|
graff |
0 |
|
|
x |
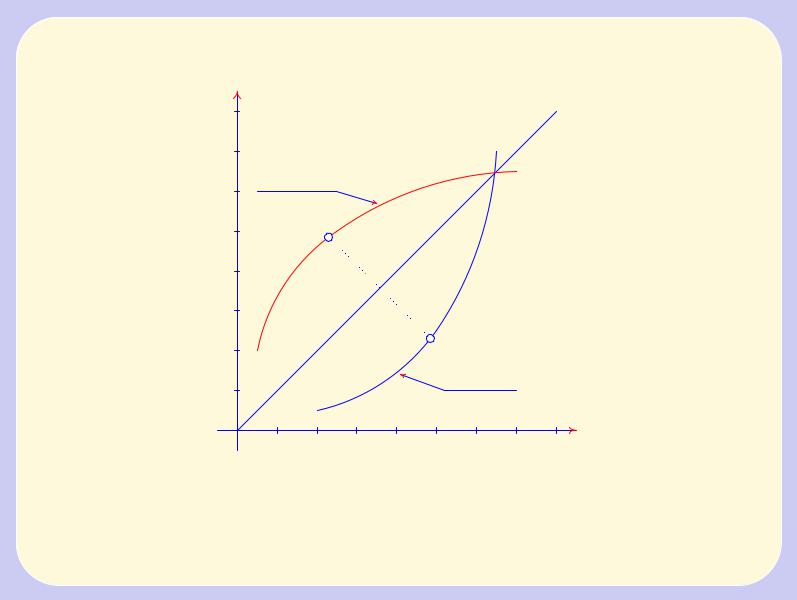
Рис. |
3.4 |
Графики |
пря- |
мой |
и |
обратной |
функций |
First Prev Next Last Go Back Full Screen Close Quit
Графики прямой и обратной элементарных
функций 
Просматривайте одновременно графики
прямой и обратной функций школьного курса математики: sin и arcsin, cos и arccos,
tg и arctg, ctg и arcctg, exp и ln,....
First Prev Next Last Go Back Full Screen Close Quit
3.1.4.Композиция отображений.
Богатым источником новых функций, с одной стороны, и способом расчленения сложных функций на более простые - с другой, является операция композиции отображений.
Если отображение f : A ! B и g : B ! C таковы, что одно из них (в нашем случае g) определено на множестве значений другого (f), то можно построить новое отображение
g f : A ! C;
значения которого на элементах множества A определяются формулой
(g f)(x) := g (f(x)) :
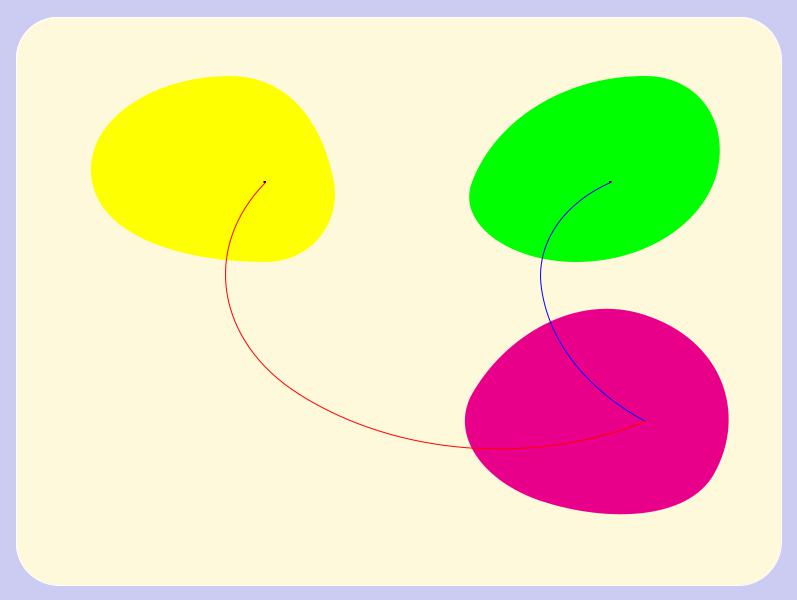
Построенное составное отображение g f : A ! C называют композицией отображения f и отображения g (см. рис. 3.5).
First Prev Next Last Go Back Full Screen Close Quit
x 
y
g
g f
z
C
Рис. 3.5 Композиция отображений
First Prev Next Last Go Back Full Screen Close Quit
Синонимы термина композиция отображений есть композиция функций, сложная функция. Очевидно, что если отображение f : A ! B биекция и отображение f-1 : B ! A обратное отображению f; то
8x 2 A : x = f-1 f(x)
и
8y 2 B : y = f f-1(y):
КОМПОЗИЦИЯ ФУНКЦИЙ Пусть графики функций f и g уже построены.
Показана схема построения графика функции f g.
При построении точек графика функции f g используется вспомогательная прямая П : y = x.
Перемещая движок “x value” Вы видите как каждой точке x оси абсцисс сопоставляется точка (x; f g(x)).
First Prev Next Last Go Back Full Screen Close Quit
3.2.Фундаментальные функции элементарной математики.
Среди функций f : A ! B; A; B R выде-
ляют фундаментальные функции. Почти все они содержатся в школьном курсе мате-
матики. К фундаментальным функциям элементарной математики относятся следующие функции:
First Prev Next Last Go Back Full Screen Close Quit
3.2.1.Линейная функция.
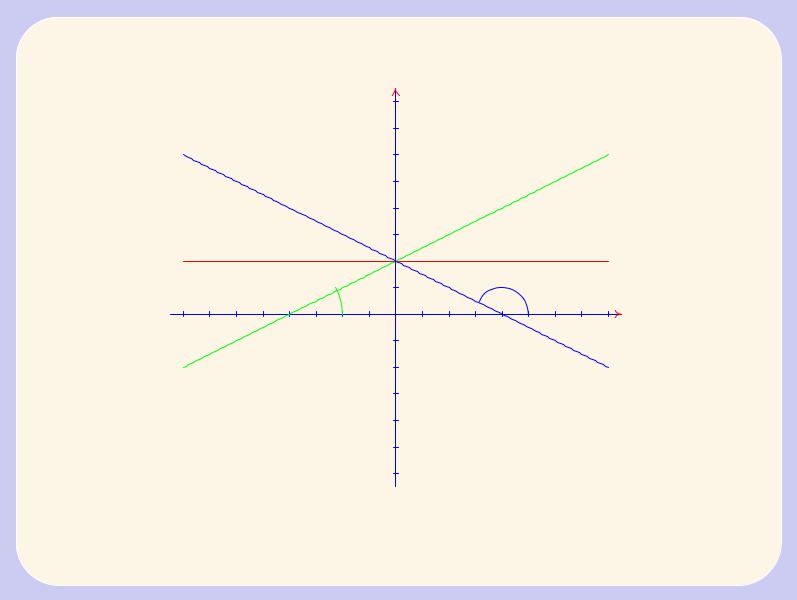
Линейная функция y = kx + b; 8x 2 R, где k и b - вещественные числа. Графиком линейной функции является прямая. Число k называется угловым коэффициентом этой прямой. Угловой коэффициент прямой равен тангенсу угла наклона этой прямой к положительному направлению оси абсцисс: k = tg : Число b называется начальной ординатой. Прямая определяется двумя точками. Точка M0(0; b) принадлежит графику линейной функции y = kx + b.
На рисунке 3.6 посмотрите графики линейной функции при различных значениях k и b = 2.
Посмотрите графики линейной функции при различных значениях коэффициентов 
По графику функции y = mx + b найдите коэффициенты m и b
First Prev Next Last Go Back Full Screen Close Quit
|
y |
|
k = -1 |
|
|
2 |
|
|
|
k = 0; = 0 |
|
|
|
|
0 |
x |
k = |
1 |
|
|
2 |
|
Рис. 3.6 Графики функции y = kx + 2 |
First Prev Next Last Go Back Full Screen Close Quit
-b 2a
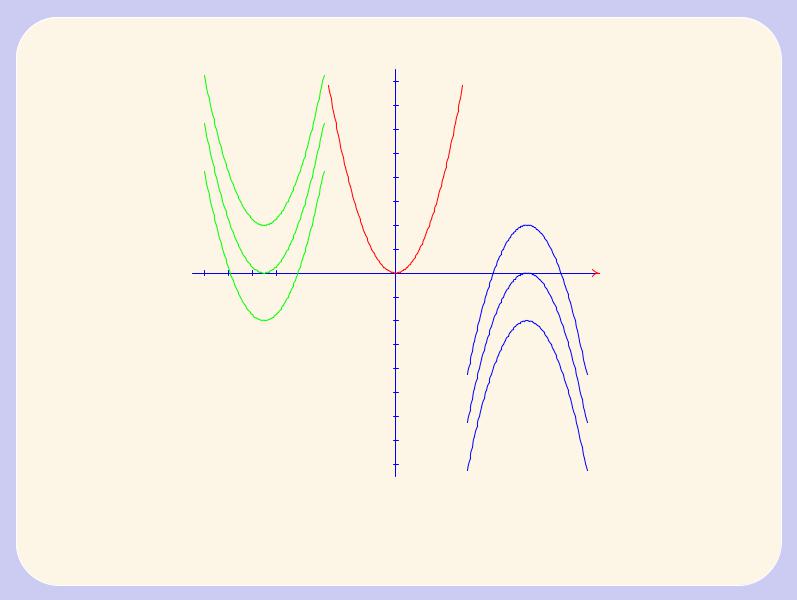
3.2.2.Квадратичная функция.
Квадратичная функция y = ax2 + bx + c; a 6= 0; 8x 2 R, где a; b; c - вещественные числа. Графиком квадратичной функции является парабола (см. рис. 3.7). Ветви параболы при a > 0 направлены в положительном направлении оси ординат (вверх); при a < 0 - в отрицательном направлении оси ординат (вниз). Выражение = b2 - 4ac называется дискрименантом квад-
ратичной функции. Если > 0, то парабола в двух точках |
|
p |
|
|
p |
пересекает ось абсцисс; если = 0, то |
x1 = |
-b- ; x2 = |
-b+ |
|
2a |
2a |
|
касается оси абсцисс в точке x0 = ; если = b2 - 4ac < 0, то парабола не имеет общих точек с осью абсцисс.
Посмотрите графики квадратичной функции при различных значениях коэффициентов 
First Prev Next Last Go Back Full Screen Close Quit
y
y = x2
< 0
a < 0
= 0
> 0
> 0 
0 
x= 0
a > 0
< 0
Рис. |
3.7 |
Графики |
квадратич- |
ной |
функции |
y = |
ax2 + bx + c |
First Prev Next Last Go Back Full Screen Close Quit
