Для всех натуральных n имеет место неравенство Бернулли
(1+x1)(1+x2) (1+xn) 1+x1+x2+ +xn;
(10.4) где x1; x2; : : : ; xn – числа одного и того же
знака, большие минус единицы. Доказательство. Обозначим через p(n) нера-
венство, которое нужно доказать. Применим метод математической индукции.
I. При n = 1; 2 неравенство (10.4) имеет место.
II. Пусть p(n) имеет место, т.е.
(1+x1)(1+x2) (1+xn) 1+x1+x2+ +xn:
III. Если неравенство (10.4) имеет место при n; то для n + 1 имеем
First Prev Next Last Go Back Full Screen Close Quit
(при xi > -1; i = 1; 2; : : : ; n; n + 1)
II:
(1 + x1)(1 + x2) (1 + xn)(1 + xn+1)
(1 + x1 + x2 + + xn) (1 + xn+1) =
=1 + x1 + x2 + + xn + xn+1+
+(x1 + x2 + + xn) xn+1
1 + x1 + x2 + + xn + xn+1:
На последнем шаге мы отбросили слагаемое
(x1 + x2 + + xn) xn+1;
которое является неотрицательным, если все xi; i = 1; 2; : : : ; n; n + 1; одного знака.
First Prev Next Last Go Back Full Screen Close Quit
Доказать, что если x > -1; то для всех натуральных n > 1 имеет место неравенство
причём знак равенства имеет место лишь при x = 0:
Доказательство.
Неравенство (10.5) есть следствие неравенства (10.4) при x1 = x2 = : : : = xn = x:
НЕРАВЕНСТВО БЕРНУЛЛИ
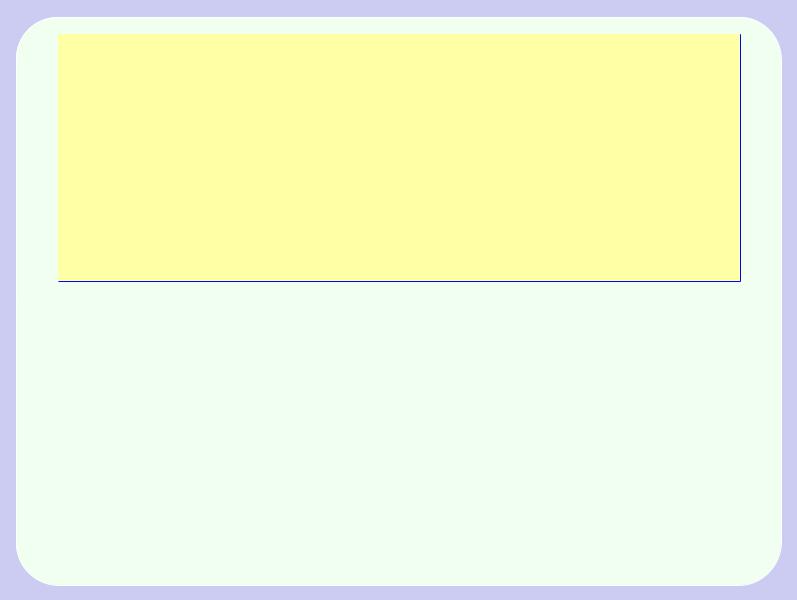
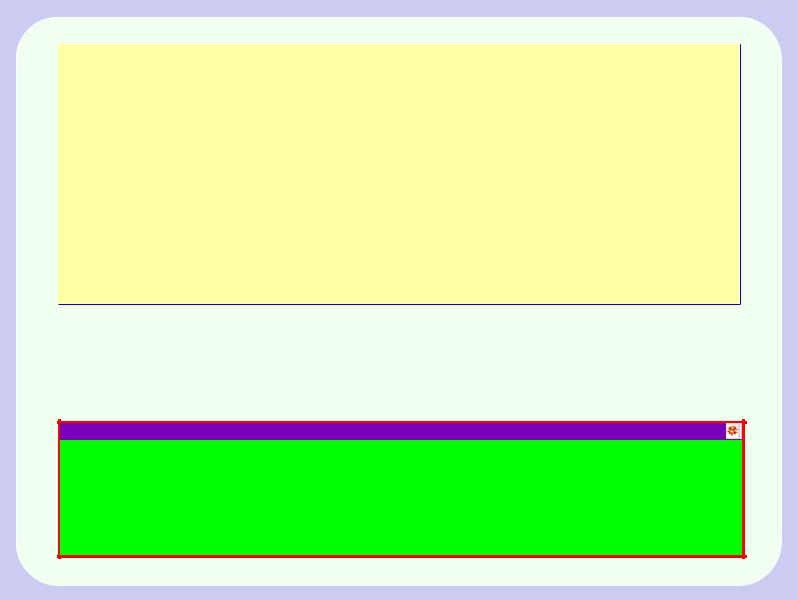
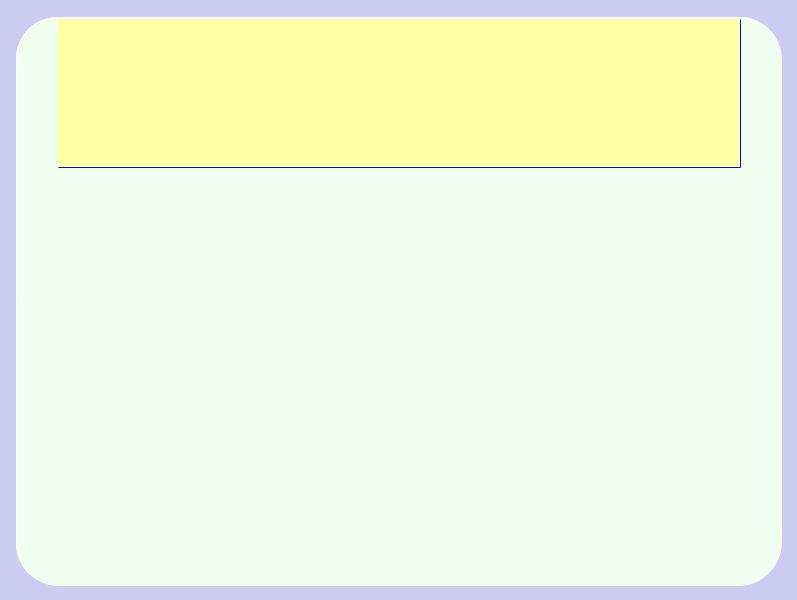
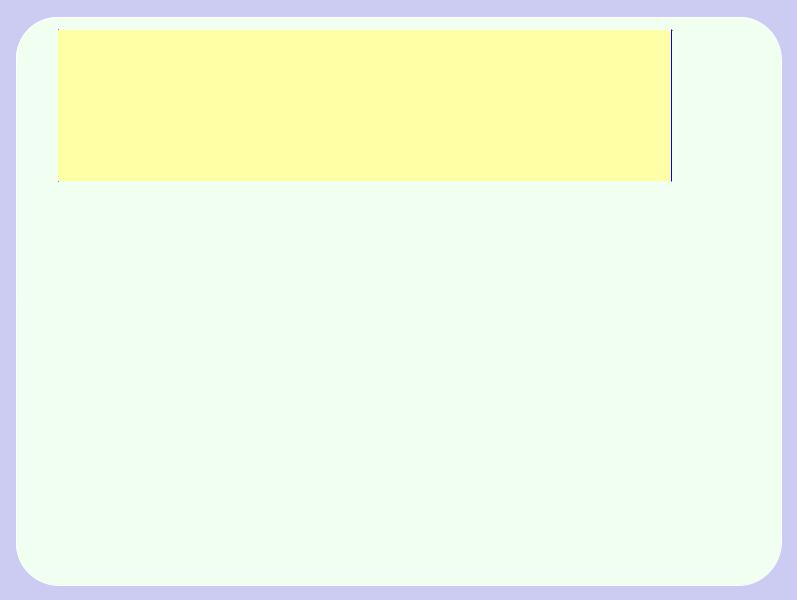
На иллюстрации показаны графики функций fn(x) = (1 + x)n (синий) и gn(x) = 1 + nx (красный) при n = 2; 3; : : : ; 10.
При всех значениях n = 2; 3; : : : ; 10, которое устанавливается движком “n”, синяя кривая всегда выше красной с единственной точкой соприкосновения (0; 1).
First Prev Next Last Go Back Full Screen Close Quit
Доказать, что если 0 < jqj < 1; то для всех натуральных n > 1 имеет место неравенство
jqnj < |
jqj |
(10.6) |
|
: |
|
|
n (1 - jqj) |
|
Доказательство.
Неравенство 10(.6) |
|
получается |
из |
|
|
следующей |
цепочки неравенств |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
n 10:5 |
|
|
= 1 + |
|
- 1 |
> |
|
jqjn |
jqj |
|
|
1 |
|
|
|
|
|
1 |
|
|
|
> 1 + n |
|
- 1 > n |
|
|
- 1 : |
jqj |
jqj |
Отсюда следует, что |
|
|
|
|
|
|
|
|
|
jqnj |
= jqjn |
< |
|
|
jqj |
|
: |
|
n (1 - jqj) |
First Prev Next Last Go Back Full Screen Close Quit
Доказать, что если b 2 R; b > 1; то для всех натуральных n > 2 имеет место неравенство
|
|
|
|
|
n |
2 |
|
|
|
|
|
(10.7) |
|
|
|
|
|
|
|
|
< |
|
|
|
|
|
: |
|
|
|
|
|
bn |
(n - 1)(b - 1)2 |
|
|
Доказательство. Так как b > 1; то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
n |
10:2 |
|
|
|
|
|
|
|
|
|
|
|
|
b = |
(1 + (b - 1)) |
= |
|
= 1 + n(b - 1) + |
|
n(n - 1) |
(b - 1)2 + + (n - 1)n > |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
n(n - 1) |
(b - 1)2: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
< |
|
|
|
2n |
|
= |
|
|
2 |
|
: |
|
|
|
|
|
|
|
|
bn |
n(n - 1)(b - 1)2 |
(n - 1)(b - 1)2 |
|
First Prev Next Last Go Back Full Screen Close Quit
jaj =
Очевидно, что
Модуль вещественного числа.
Определение 171. Абсолютной величиной (модулем) вещественного числа a, обозначение jaj; называется число, равное a; если
a 0; и равное -a; если a < 0; т.е.
a; если a 0;
-a; если a < 0:
jaj = maxf-a; ag:
First Prev Next Last Go Back Full Screen Close Quit
10.3.Геометрическая прогрессия
Если b0 – первый член, а q 6= 1 – постоянное отношение следующего члена к предыдущему, называемое знаменателем геометрической прогрессии, то
bj = b0qj; (j = 1; 2; 3; : : :);
n |
n |
|
|
|
|
|
X |
X |
|
1 - qn+1 |
|
b0 - bnq |
|
Sn = b = b qj |
= b |
|
= |
|
: |
j |
0 |
0 |
1 - q |
|
1 - q |
j=0 |
j=0 |
|
|
|
|
|
|
|
|
|
(10.8) |
First Prev Next Last Go Back Full Screen Close Quit
10.4. Алгебра.
Квадратичная форма.
Пусть x = (x1; x2; : : : ; xn)T 2 Rn: Функция
Xn
(x) := aijxixj;
i;j=1
где aij = aji; aij 2 R; называется квадратичной формой на Rn: Матрица (aij) 2 Mnn(R) называется матрицей квадратичной формы.
Квадратичная форма называется знакоопределённой, если онаположительноилиотрицательно определённая.
First Prev Next Last Go Back Full Screen Close Quit
Положительно определенная квадратичная |
|
|
|
|
форма. |
|
|
|
|
|
|
|
Квадратичная |
форма |
n |
a |
ij |
xixj; a |
ij |
= a |
ji |
; |
|
|
|
i;j=1 |
|
|
|
|
называется |
положительно определённой, если |
|
|
P |
|
|
|
|
|
|
|
при любых не равных одновременно нулю значе-
ниях переменных Pn aijxixj > 0.
i;j=1
Отрицательно определенная квадратичная |
|
|
|
|
форма. |
|
|
|
|
|
|
|
Квадратичная |
форма |
n |
a |
ij |
xixj; a |
ij |
= a |
ji |
; |
|
|
|
i;j=1 |
|
|
|
|
называется |
отрицательно определённой, если |
|
|
P |
|
|
|
|
|
|
|
при любых не равных одновременно нулю значе-
ниях переменных Pn aijxixj < 0.
i;j=1
First Prev Next Last Go Back Full Screen Close Quit
Критерия Сильвестра.
Квадратичная форма Pn aijxixj; aij = aji; с
i;j=1
симметрической матрицей
положительно определенатогда и только тогда, когда положительны всеглавные минорыэтой матрицы; формаотрицательно определенатогда
и только тогда, когда a11 < 0, и при переходе от любогоглавного минораматрицы к главному минору следующего порядка знак значения минора меняется.
First Prev Next Last Go Back Full Screen Close Quit