Введение в математический анализ. Дифференциальное исчисление

Тогда:

1. если D(x0; y0) > 0, то в точке M0(x0; y0) функция f имеет экстремум:

строгий минимум, если @2f(x02;y0) > 0;

@x

строгий максимум, если @2f(x02;y0) < 0;

@x

2. если D(x0; y0) < 0, то в точке M0(x0; y0) функция f экстремума не имеет;

3. если D(x0; y0) = 0, то экстремум в точке M0(x0; y0) может быть, а может и не быть. Эта теорема есть частный случай (n = 2) теоремы 121.

First Prev Next Last Go Back Full Screen Close Quit

Пример 131. Исследовать на экстремумы функцию

f(x; y) = x3 + 3y2 - 3xy:

First Prev Next Last Go Back Full Screen Close Quit

Частные производные второго порядка

@2f(x; y) = @ 3x2 - 3y = 6x; @x2 @x

@2f(x; y) = @ (6y - 3x) = 6; @y2 @y

@2f(x; y) = @ (6y - 3x) = -3 @x@y @x

непрерывны в R2 и

D(x; y) = (6x) 6 - (-3)2 = 36x - 9:

Неравенство D(0; 0) = -9 < 0 показывает, что в точке O(0; 0) экстремума нет (см. пункт 2 теорема 122).

First Prev Next Last Go Back Full Screen Close Quit

Вычисляя D(12; 14) = 9 > 0; заключаем, что в

точке M0 12; 14 функция f имеет экстремум.

Так как @2f(M0) = 3 > 0; то M0 – точка стро-

@x2

гого минимума и

(см. пункт 1 теорема 122).

First Prev Next Last Go Back Full Screen Close Quit

6.10.4.Наибольшее и наименьшее значения функции двух

переменных.

Если функция f : D ! R; D R2 непрерывна в ограниченной замкнутой области D, то, в силу второй теоремы Вейерштрасса, она

принимает в этой области своё наибольшее и наименьшее значения.

First Prev Next Last Go Back Full Screen Close Quit

Для нахождения наибольшего и наименьшего значений функции f : D ! R нужно:

найти все стационарные точки функции f внутри области D;

найти внутренние точки области D; в которых функция f недифференцируема;

вычислить значения функции f в этих точках;

найти наибольшее и наименьшее значения функции f на границе области D;

из всех полученных таким образом значе-

ний выбрать наибольшее и наименьшее.

First Prev Next Last Go Back Full Screen Close Quit

Пример 132. Найти наибольшее и наименьшее значения функции

f(x; y) = x3 + 3y2 - 3xy

в области

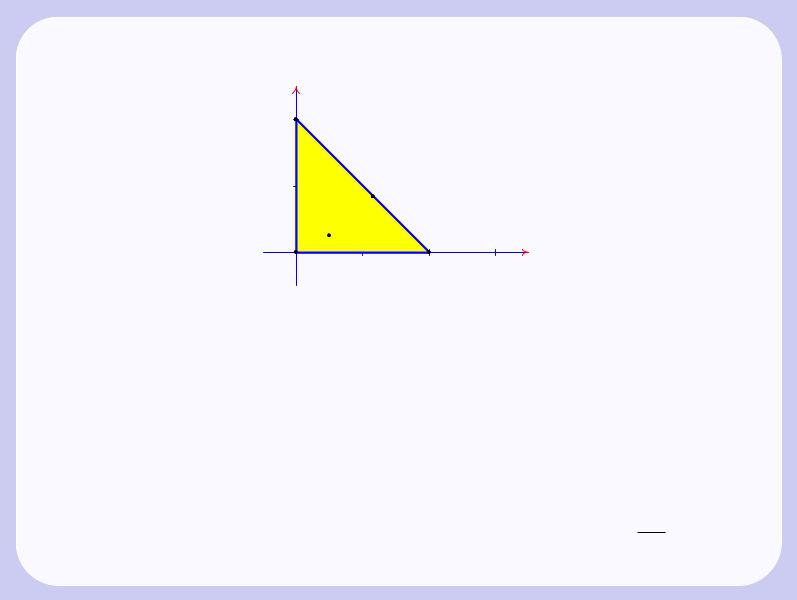
D := f(x; y) 2 R2 j 0 x; 0 y; x + y 2g:

First Prev Next Last Go Back Full Screen Close Quit

Находим наибольшее и наименьшее значения функции f на границе области D :

– Вычисляем f(0; 2) = 12; f(2; 0) = 8:

– На границе OA : x = 0; 0 < y < 2; получаем '(y) = f(0; y) = 3y2; 0 < y < 2: Функция ' монотонно возрастает на (0; 2); следовательно

x3; 0 < x < 2: Функция монотонно возрастает на (0; 2); следовательно

– На границе AB : y = 2 - x; 0 < x < 2; получаем (x) = f(x; 2 - x) = x3 + 3(2 - x)2 - 3x(2 - x) = x3 + 6x2 - 18x + 12; 0 < x < 2:

First Prev Next Last Go Back Full Screen Close Quit