Введение в математический анализ. Дифференциальное исчисление

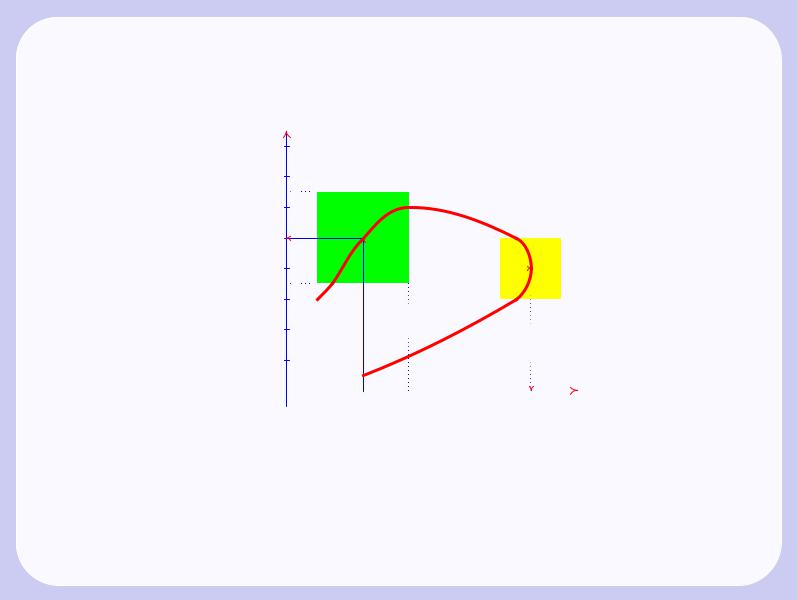
6.7.1.Неявно заданные функции одной переменной.

Пусть задана кривая L : F(x; y) = 0. Рассмот-

где M0(x0; y0) 2 L.

First Prev Next Last Go Back Full Screen Close Quit

y1 y0 -

L

First Prev Next Last Go Back Full Screen Close Quit

Обозначим через LD := L\D часть кривой L, попавшую в D. Если LD удовлетворяет условию, что всякая прямая параллельная оси Oy пересекает LD не более чем в одной точке, то LD есть график некоторой функции

f : (x0 - ; x0 + ) ! (y0 - ; y0 + );

которая называется функцией неявно заданной уравнением F(x; y) = 0 в области

D.

First Prev Next Last Go Back Full Screen Close Quit

Если же LD удовлетворяет условию, что всякая прямая параллельная оси Ox пересекает LD не более чем в одной точке, то LD есть график некоторой функции

g : (y0 - ; y0 + ) ! (x0 - ; x0 + );

которая тоже называется функцией неявно заданной уравнением F(x; y) = 0 в области

D.

First Prev Next Last Go Back Full Screen Close Quit

Если f : (x0 - ; x0 + ) ! (y0 - ; y0 + )

задана неявно уравнением F(x; y) = 0 в области D, то

8x 2 (x0 - ; x0 + ) : F (x; f(x)) 0: (6.20)

First Prev Next Last Go Back Full Screen Close Quit

6.7.2.Производная неявно заданной функции одной

переменной.

где M0(x0; y0) 2 L.

First Prev Next Last Go Back Full Screen Close Quit

Теорема 114. Пусть:

1. функция F определена и непрерывна вместе со своими частными произ- водными в некоторой U"(M0), где

M0(x0; y0);

2. F(x0; y0) = 0;

3. @F(M0) 6= 0; @y

First Prev Next Last Go Back Full Screen Close Quit

Тогда:

4. в некотором прямоугольнике D U"(M0) уравнение F(x; y) = 0 задаёт неявно функцию f : (x0 - ; x0 + ) ! (y0 - ; y0 + );

5.f(x0) = y0;

6.функция f непрерывно дифференцируема

на интервале (x0 - ; x0 + ), причём

@F(x;f(x))

8x 2 (x0 - ; x0 + ) : f0(x) = - @x :

@F(x;f(x)) @y

Доказательство теоремы в данном курсе не рассматривается.

First Prev Next Last Go Back Full Screen Close Quit

6.7.3.Касательная и нормаль к плоской кривой.

где M0(x0; y0) 2 L.

First Prev Next Last Go Back Full Screen Close Quit

Пусть в некоторой U"(M0) существуют непрерывные частные производные @x@F; @y@F и

6= 0. Тогда, в силу теоремы 114, в прямоугольнике D U"(M0) уравнение F(x; y) = 0 задаёт неявно функцию

f: (x0 - ; x0 + ) ! (y0 - ; y0 + );

кграфику которой можно провести касательную в точке M0

First Prev Next Last Go Back Full Screen Close Quit