Файловый архив студентов. Файловый архив студентов.
1305 вузов, 5165 предметов.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Томский Государственный Университет Систем Управления и Радиоэлектроники
Предмет:
[НЕСОРТИРОВАННОЕ]
Файл:

Прикладная математическая статистика

..pdf
Скачиваний:
10
Добавлен:
05.02.2023
Размер:
5.67 Mб
Скачать
☆

 

 

 

71

получают числа

x

ji

при упорядочении всей их совокупности. Ранговые критерии

 

 

 

применяются и тогда, когда измерения сделаны в порядковой шкале, например,

представлены текстовыми баллами или экспертными суммами. Здесь значения

x

ji

вообще

 

 

 

являются условностью, а содержательный смысл имеют лишь отношения «больше — меньше» между ними (например, оценки 2, 3, 4, 5). Будем рассматривать наиболее простой

случай, когда среди чисел

x

ji

 

нет совпадающих. В этом случае преобразование таблицы 6.1 в

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

таблицу 6.4 будет однозначным.

 

 

 

 

 

 

 

 

 

 

Для проверки

гипотезы

 

H

0

необходимо сконструировать некоторую

статистику, т.е.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

функцию от рангов r

ji

, которая легла бы в основу критерия проверки гипотезы. Основные

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

требования к этой статистике следующие: ее значение при гипотезе

H0

должно заметно

отличаться от ее значений при альтернативах. Рассмотрим два метода.

 

 

Таблица 6.4. Форма представления преобразованных

 

 

 

 

данных

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Ранги

 

 

 

 

 

 

 

 

 

Уровни фактора

A

 

 

 

 

результатов

 

 

A

 

 

 

 

 

A

 

A

 

 

A

 

 

 

 

наблюдений

 

 

 

1

 

 

 

 

 

2

 

i

 

 

k

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

r

 

 

 

 

 

r

r

 

 

r

 

 

 

 

 

 

 

 

 

 

 

 

1i

 

1k

 

 

 

 

 

 

 

11

 

 

 

 

12

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

r

 

 

 

 

 

 

 

r

 

 

r

 

 

 

 

 

 

 

 

 

 

 

 

r

 

2i

 

2 k

 

 

 

 

 

 

 

21

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

22

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

….

 

 

 

….

 

 

 

 

….

….

 

 

….

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

j

 

 

 

r

j1

 

 

 

 

r

j 2

r

ji

 

r

jk

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

….

 

 

 

….

 

 

 

 

…..

…..

 

…..

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

n

 

 

 

r

 

 

 

 

 

r

 

r

 

 

r

 

 

 

 

 

 

 

 

n 1

 

 

 

 

n 2

n i

 

n k

 

 

 

 

 

 

 

 

1

 

 

 

 

 

2

 

i

 

k

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Однофакторный непараметрический анализ на основе критерия Краскела-Уоллеса (произвольные альтернативы)

Этот метод используется, когда невозможно сказать что-либо определенное об альтернативах H0 , так как он свободен от распределения. Заменим наблюдения x ji их

рангами rji , упорядочивая всю совокупность x ji в порядке возрастания. Затем для каждой

обработки i (уровня фактора,

столбца таблицы) надо вычислить суммарный и средний

ранги:

 

 

 

 

 

 

 

 

 

 

ni

 

 

 

1

ni

 

 

Ri rji

и

R

i

rji .

(6.11)

 

n

 

 

j 1

 

 

 

j 1

 

 

 

 

 

 

i

 

Если между столбцами нет систематических различий, то средние ранги

Ri , не должны

значительно отличаться от среднего, рассчитанного по всей совокупности

rji . Значение

последнего R

N 1

. Здесь N — общее число наблюдений.

 

2

 

 

 

 

 

 

 

 

 

72

Nni .

i 1k

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Вычислим

 

величины

(Ri R)2

для

каждого

уровня

фактора

 

 

 

N 1

2

 

 

 

N 1

2

 

 

 

 

 

 

 

 

 

 

 

Ri

 

 

 

,..., Rk

 

 

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

2

 

 

 

 

 

 

Эти значения при

H

0

 

в совокупности должны быть небольшими. Составляя общую

характеристику, разумно учесть различия в числе наблюдений для разных обработок (уровней факторов) и взять в качестве меры отступления от чистой случайности величину

 

12

n

 

 

 

N 1

 

2

 

 

 

 

H

 

n

Ri

 

 

 

 

 

 

 

 

N (N 1)

i

 

2

 

 

i 1

 

 

 

 

 

Эта величина называется статистикой Краскела-Уоллеса

.

(6.12)

Множитель

12

присутствует в качестве нормировочного для обеспечения сходимости

 

N(N 1)

 

 

 

 

 

 

распределения статистики H и

2

с числом степеней свободы v k 1. Если

H

 

2

(v) ,

 

q

 

 

 

 

 

 

 

 

то фактор считается значимым и гипотеза H0 отвергается при уровне значимости

q .

 

 

 

Если среди

x ji

есть совпадающие значения, то при ранжировании и переходе к

rji

надо

использовать средние ранги (например, если 2 значения (5 и 5) занимают ранги 11, 12, то средний ранг (11,5) надо присвоить им обоим). Если совпадений много, рекомендуется

использовать модифицированную форму статистики

H

:

H

 

 

H

 

 

 

m

 

 

 

 

 

 

 

1

Tj

/(N

3

N )

 

 

 

 

j 1

 

 

 

,

(6.13)

где m — число групп наблюдений в группе j

совпадающих наблюдений; T

j

r3

t

j

( t

j

— число совпадающих

 

j

 

 

 

).

 

 

 

 

 

 

 

Однофакторный непараметрический анализ на основе критерия Джонкхиера (альтернативы с упорядочением)

по

Нередко исследователю заранее известно,

что имеющиеся группы результатов упорядочены

возрастанию влияния фактора. Пусть

первый столбец таблицы

x

ji

 

соответствует

 

 

 

 

 

наименьшему уровню, а последний — наибольшему. В таких случаях критерий Джонкхиера более чувствителен (более мощный) в сравнении с упорядоченным влиянием фактора.

Рассмотрим сначала случай, когда сравниваются только 2 способа обработки (2 уровня фактора). Фактически речь идет тогда об однородности двух выборок. Для проверки этой гипотезы рассмотрим статистику Манна-Уитни.

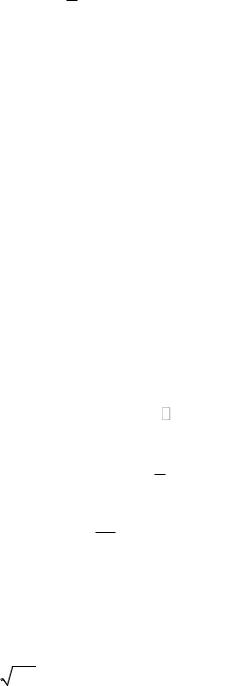
Пусть имеем 2 выборки: x1, x2 ,...., xm и y1, y2 ,..., yn . Положим

73

 

 

 

0,

åñëè x

 

 

 

 

 

 

 

i

 

 

 

 

 

 

 

 

(x , y

)

1

, åñëè x

 

 

 

i

j

 

 

 

i

 

 

 

 

2

åñëè x

 

 

 

1,

 

 

 

 

 

 

 

i

 

Статистика Манна-Уитни:

 

 

 

 

 

 

 

 

 

m n

 

i

 

 

 

 

 

 

 

 

U

 

 

(x ,

 

 

 

 

 

i 1 i 1

 

 

y

j

;

 

 

y

j

;

 

 

y

j

.

 

 

y

j

)

 

 

.

(6.14)

(6.15)

Обратившись теперь к общему случаю, когда сравниваются

k

уровней), поступим следующим способом.

Для

каждой пары

1 u v k , составим по выборкам с номерами u

 

и v

статистики

 

m

n

 

i

j

 

 

 

U (u,v)

 

 

 

 

 

 

 

(x , y

 

) .

 

 

i 1

i 1

 

 

 

 

 

 

способов обработки ( k

уровней

u

и

v , где

Манна-Уитни:

(6.16)

Получим

U (1,2), U (1,3),...,U (1,k), U (2,3),...,U (2,k),...,U (k

1,k)

.

Определим статистику Джонкхиера

I

как

I

 

U (u,v)

для

1 u

v

k

. Свидетельством

против

H

0

 

(в пользу альтернативы

H

1

 

)

служат большие значения статистики

I

,

полученные в эксперименте. Для больших объемов выборок в отношении статистики

I

действует

нормальное распределение

 

I

 

N (MI ,

DI )

,

 

с

математическим ожиданием

и

дисперсией

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

k

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

MI

 

 

N

2

n

j

,

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

4

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

i 1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

k

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

DI

 

 

N

2

(2N 3)

 

n

2

(2n

 

3)

 

,

(6.17)

 

 

 

 

 

 

 

72

 

j

j

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

j 1

 

 

 

 

 

 

 

 

 

 

 

 

где n

j

– количество наблюдений в каждом уровне;

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

N

— общий объем наблюдений;

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Свидетельством против H0 (в пользу альтернативы H1 ) служат большие значения

статистики

I *

I MI

 

, полученные

 

в

эксперименте,

в

 

сравнении с

-процентными

 

 

 

 

 

 

 

 

 

 

 

 

 

DI

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

точками нормального распределения

(I

)

*

 

(табличные значения нормированной

функции Лапласа). Тогда

q 1

— уровень значимости принятия гипотезы H0 .

6.3. Двухфакторный анализ

Иногда в однофакторной модели влияние интересующего нас фактора не проявляется, хотя такое влияние должно быть. Причиной этого может быть большой внутригрупповой разброс, на фоне которого действие фактора остаётся незаметным. Очень часто этот разброс вызван не только случайными причинами, но и действиями еще одного фактора. Если мы в состоянии указать такой фактор, то можно попытаться включить его в модель, чтобы уменьшить статистическую неоднородность наблюдений. Конечно, не всегда удается поправить дело введением мешающего фактора и переходом к двухфакторной схеме. Иногда

74

приходится рассматривать трехфакторные и более сложные модели. Замысел во всех этих

случаях остается прежним.

 

 

 

Назовём фактор A

(рис. 1) главным,

B — мешающим. Пусть фактор A

принимает k

значений, а мешающий — n значений. Фактор

B разбивает все группы

наблюдений

(столбцы таблицы x

ji

) на блоки.

 

 

 

 

 

 

 

 

Рис. 6.1.

Двухфакторная модель

 

Каждый блок соответствует определенному уровню фактора

B . В частном случае таблица

содержит

n k

наблюдений (по одному в клетке). Отличие этой таблицы от однофакторной

в том, что наблюдения в любом столбце не являются однородными, если влияние мешающего фактора значимо (табл. 6.3).

Таблица 6.3

Форма представления экспериментальных данных двухфакторной модели

Блоки фактора

Уровни основного фактора A

 

 

 

 

 

 

B

 

 

A

 

A

 

A

A

 

 

 

 

 

 

 

 

1

 

 

2

 

 

 

i

 

 

k

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

B

 

 

 

x

 

 

 

x

 

 

x

 

 

x

 

 

 

 

 

 

 

 

 

 

 

 

1i

1k

 

 

1

 

 

11

 

12

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

B

 

 

 

x

21

 

x

 

 

x

2i

x

2 k

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

22

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

….

 

….

 

 

 

….

 

 

….

 

 

….

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

B

j

 

 

x

j1

 

x

j 2

 

x

ji

x

jk

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

….

 

….

 

 

 

…..

 

 

…..

 

 

…..

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

B

n

 

 

x

n1

 

x

 

 

x

ni

x

 

 

 

 

 

 

 

 

 

n 2

 

 

nk

 

 

 

 

 

 

 

 

 

 

Для описания двухфакторного эксперимента обычно применяют аддитивную модель. Она

предполагает, что значения отклика x ji

являются суммой вкладов соответствующих уровней

факторов

A и B

и независимых случайных факторов: xji ai bj eji . В этой модели

величины вкладов

A

 

и

B не могут быть восстановлены однозначно. Действительно,

при

одновременном увеличении всех ai на одну и ту же константу и при уменьшении всех bj

на

ту же константу значения x ji не изменяются.

 

 

 

 

 

 

 

Для однозначности вкладов удобно перейти к представлению в виде:

xji i j , ï ðè i 0, j

0 .

 

i

j

 

 

Параметр интерпретируется как среднее всех

 

 

 

а i

и j — отклонения от

x ji (т.е. x ),

в результате действия факторов A и B .

75

6.3.1 Двухфакторный параметрический дисперсионный анализ

Если есть основания предполагать, что случайные величины

e

ji

 

имеют нормальное

распределение с нулевым средним и одинаковой при всех

i

и j

дисперсией

 

2

, можно

 

использовать метод, аналогичный однофакторному дисперсионному анализу. Предположим,

что влияние фактора

A

отсутствует. Сформулируем гипотезу

H0 : 1 2

... k .

Проверим гипотезу

H

0

 

,

также основываясь на сравнении двух независимых оценок

дисперсии: 2A и ñë2 .

Дисперсионный анализ для двухфакторных таблиц

последовательности. Вычисляются суммы (полагаем n1 n2

 

k

 

 

1

k

 

n

 

2

 

1

n

 

k

 

2

 

 

 

 

 

 

2

 

 

 

 

 

n

 

 

 

 

 

 

 

 

 

 

 

Q1 x ji ; Q2

 

n

 

x ji

; Q3

 

 

 

x ji ; Q4

 

k

i 1

j 1

 

i 1

 

j 1

 

 

 

j 1

i 1

 

 

 

Далее находятся оценки дисперсий

проводится

... nk

n )

 

 

1

k

n

 

2

 

 

x ji

 

 

nk i 1

j 1

 

 

вследующей

.

s

2

ñë

 

 

Q Q

 

Q

 

Q

 

1

 

4

 

2

 

3

 

 

 

 

 

 

(k 1)(n 1)

 

;

s

2

 

Q

2

Q

4

 

 

 

A

 

 

k 1

 

 

 

 

 

 

;

s

2

 

Q

3

Q

4

 

 

 

 

 

 

 

B

 

 

k 1

 

 

 

 

 

 

.

Если выполняется неравенство

s

2

 

v

 

(n 1)(k 1) , то

 

 

 

A

F

k 1, v

H0

отвергается и влияние фактора

 

 

2

s

q

1

2

 

 

 

 

 

 

 

 

 

 

 

 

ñë

 

 

 

 

 

 

 

считается существенным.

 

 

 

 

Аналогично значимым признается влияние фактора

B

, если

 

A

s

2

B

 

s

2

 

ñë

F

v

n 1, v

q

1

2

(n 1)(k

1)

.

6.3.2. Двухфакторный непараметрический анализ

Двухфакторный непараметрический анализ используется при проверке гипотезы

H

0

 

, если

о распределении случайной величины

e

ji

 

известно только то, что она непрерывна и

независима. Рассмотрим решение задачи с использованием критерия Фридмана, который не предъявляет требований к упорядочению уровней факторов.

Двухфакторный непараметрический анализ по критерию Фридмана (произвольные альтернативы)

Критерий основан на идее перехода от значений x ji к их рангам

 

однофакторного анализа ранжирование происходит не по всей таблице

 

т.е. рассматривается каждая отдельная строка таблицы. При фиксированном

rji . В отличие от

x

ji

, а по блокам,

 

 

j

 

осуществляется

ранжирование величин x ji при i 1,2,...,k . Тем самым устраняется влияние мешающего

фактора B , значение которого для каждой строки постоянно. Обозначим полученные ранги величин x ji через rji . Ясно, что rji . изменяются от 1 до k , а каждая строка представляет

76

перестановку чисел

гипотезе

H0 : 1

1,2,...,k

 

2

...

 

 

(при совпадении x

ji

надо использовать средние ранги). При

 

 

 

 

 

k

все

k !

перестановок равновероятны. Введем величину

 

 

1

n

ri

rji — среднее значение ранга по столбцу. При H0 значение для каждого столбца не

n

 

 

j 1

должно сильно отличаться от

r

k 1

2

 

— среднего ранга всех элементов таблицы.

Статистика Фридмана имеет следующий вид

 

 

 

 

 

 

12n

 

k

 

2

 

 

 

 

 

 

S

 

ri r

 

 

 

 

 

 

k(k

1)

.

(6.19)

 

 

 

 

 

 

i 1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Гипотеза

H0

отвергается в пользу альтернативы о наличии эффектов в обработке, если

S

2

(v k 1)

. Для небольших значений

n, k

величина критерия Фридмана

S(q,n,k)

q

 

 

 

 

 

 

 

 

 

 

 

может быть найдена по специальным статистическим таблицам.

Двухфакторный непараметрический анализ по критерию Пейджа (альтернативы с упорядочением)

Если уровни факторов

в таблице

x

ji

упорядочены, то

 

 

 

 

 

 

 

 

H0 : 1 2 ... k

против альтернативы

H1 : 1 2 ... k

Пейджа.

 

 

 

 

 

 

 

 

 

 

n

 

 

 

 

 

 

Введем величину R

 

 

r

ji

.

 

 

 

i

 

 

 

 

 

 

 

 

j 1

 

 

 

 

 

 

Вычисляется статистика

для проверки гипотезы

используется статистика

Li Ri

i 1k

1 R

2 R

1

2

3 R3

...

k

Rk

.

(6.20)

H

0

отклоняется в пользу H

1

, если

L

L (k, n) , где значение L

(k, n)

найдено по

 

 

 

í àáë

 

 

 

 

специальным статистическим таблицам.

 

 

 

 

 

Критические значения L (k, n) приведены в табл.

9 (см. статистические таблицы в

приложении). Для n 10 справедлива аппроксимация статистики Пейджа

 

 

L*

При

L M ( D(L

L u

 

*

 

 

 

L)

, где M (L)

nk(k 1)2

 

 

, D(L)

)

4

 

 

нулевая гипотеза отклоняется ( u

n(k 3 k)2 .

144(k 1)

–квантиль стандартного нормального

распределения.

Вопросы для самопроверки

1.Дисперсионный анализ зависимостей. Основные понятия.

2.Однофакторный параметрический дисперсионный анализ.

77

3.Однофакторный непараметрический анализ на основе критерия Краскела-Уоллеса (произвольные альтернативы).

4.Однофакторный непараметрический анализ на основе критерия Джонкхиера (альтернативы с упорядочением)

5.Двухфакторный дисперсионный анализ. Двухфакторный параметрический дисперсионный анализ.

6.Двухфакторный непараметрический анализ по критерию Фридмана (произвольные альтернативы).

7.Двухфакторный непараметрический анализ по критерию Пейджа (альтернативы с упорядочением).

78

Тема 7. Корреляционный анализ

Корреляционный анализ имеет своей задачей количественное определение тесноты связи между изучаемыми явлениями. Корреляционная связь — эта связь, при которой определенному значению факторного признака соответствует среднее значение результирующего признака. Изучение тесноты и направления связи является важной задачей математической статистики. Оценка тесноты связи между признаками предполагает определение меры соответствия вариации результирующего признака от одного (при изучении парных зависимостей) или нескольких (множественных) факторных признаков.

7.1. Вычисление параметрических коэффициентов корреляции

Выборочный коэффициент корреляции между двумя случайными величинами

x

и

y

был

впервые введен Пирсоном, поэтому его часто называют коэффициентом корреляции Пирсона. В теории разработаны и на практике применяются различные модификации формулы расчета данного коэффициента. Приведем некоторые из них:

 

 

 

 

 

 

r

(x x)( y y)

 

xy x y

.

 

 

 

 

 

 

 

 

 

 

s

s

 

 

 

 

 

s

 

s

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

y

 

 

 

 

 

 

y

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x

 

 

 

 

 

 

x

 

 

 

 

 

Используя преобразование, получают

 

 

 

i

 

 

 

 

i

 

 

 

 

 

 

 

i

 

 

 

i

 

 

 

 

 

 

 

 

 

 

 

 

 

n

 

 

 

 

 

 

 

 

 

 

n

 

 

 

 

 

 

 

 

 

 

 

 

 

r

 

x x

 

y

y

 

 

 

 

 

 

x x

 

y

 

y

 

.

i 1

 

n s s

 

 

 

 

 

 

i 1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

n

 

 

 

 

n

 

 

 

 

 

 

 

 

 

 

 

x

y

 

 

 

 

 

 

 

i

x

 

 

 

i

y

 

 

 

 

 

 

 

 

 

 

 

 

 

x

 

 

 

 

 

y

 

 

 

 

 

 

 

 

 

 

 

 

 

i 1

 

 

 

 

 

i 1

 

 

 

 

 

При n 15

необходимо скорректировать коэффициент корреляции

 

 

 

 

 

 

 

 

 

 

 

 

1 r

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

r

*

r 1

 

 

 

 

 

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2(n 3)

 

 

 

 

 

 

 

 

 

 

(7.1)

(7.2)

При большом объеме выборки выборочный коэффициент корреляции будет приближаться к корреляционному моменту генеральной совокупности , который определяется как

M (x m

 

)( y m )

 

x

 

y

 

 

 

y

 

x

 

 

.

(7.3)

Если r 0, то величины x и y независимы, является функциональной. Коэффициент корреляции

а при

r 1

зависимость между x и

y

тесно связан с коэффициентом регрессии:

 

 

 

 

 

r b

sx

,

 

 

 

 

 

 

 

(7.4)

 

 

 

 

 

sy

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

где b — коэффициент регрессии в уравнении вида yi

a bxi ;

 

sx

— среднеквадратичное отклонение x ;

 

 

 

 

 

 

sy

— среднеквадратичное отклонение y . Значимость коэффициента корреляции проверяется

на основе критерия Стьюдента. При проверке этой гипотезы вычисляется t -статистика:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

r (n 2)

 

 

 

 

 

r

 

 

 

 

 

t

 

 

 

 

 

 

 

 

n 2 .

(7.5)

 

pac

1 r2

 

 

 

 

 

 

 

 

 

 

 

r2

 

 

 

 

1

 

 

 

 

79

 

 

 

 

Расчетное значение сравнивается с табличным значением

t

q

(v n 2)

. Если расчетное

 

 

 

 

значение больше табличного, это свидетельствует о значимости коэффициента корреляции,

а, следовательно, и о статистической существенности зависимости между

x

и

y .

 

При большом числе наблюдений ( n 100 ) используется следующая

формула

t -

статистики:

 

 

 

 

t

pac

 

 

 

r

n

1 r

 

2

 

.

(7.6)

Множественный коэффициент корреляции рассчитывается при наличии линейной связи между

результирующим признаком

Y

и несколькими факторными признаками, а также между

парой факторных признаков.

 

 

 

 

 

 

 

 

 

 

 

В случае оценки связи между

 

результирующим признаком

Y

и двумя факторными

признаками

x1 и

x2

множественный

 

коэффициент корреляции

можно определить по

формуле:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

r

2

r

2

2r

r

r

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

R

 

 

 

yx

yx

 

 

yx

yx

x x

 

,

 

(7.7)

 

 

 

 

1

 

 

2

 

1

2

1

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

y / x ,x

 

 

 

 

1 r

2

 

 

 

 

 

 

 

 

 

 

1

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

2

 

 

 

 

 

 

где rab — парные коэффициенты корреляции между признаками.

В общем случае коэффициент множественной корреляции между результирующим признаком Y и m факторными признаками x1, x1,..., xm определяется по формуле

R

 

 

 

 

1

 

y / x

,x

,...,x

 

 

1

2

 

m

 

 

 

 

 

 

 

 

 

 

 

1

,

(7.8)

где

– определитель матрицы парной корреляции

 

 

 

 

 

1

 

 

yx

 

yx

...

 

yx

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

2

 

 

 

m

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x y

 

 

1

 

x x

...

x x

m

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

1

2

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

...

 

 

 

 

;

(7.9)

 

 

 

x

y

x x

 

 

x x

 

 

 

 

 

2

 

 

 

 

2

1

 

 

 

 

 

 

 

2

m

 

 

 

 

 

...

 

 

...

...

... ...

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

...

 

 

1

 

 

 

 

 

 

 

 

x

y

x

x

x

x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

m

 

 

 

 

m

2

 

 

m

3

 

 

 

 

 

 

 

 

 

– алгебраическое дополнение элемента .

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

11

 

 

 

 

 

Множественный коэффициент корреляции изменяется в пределах от 0 до 1. Приближение

R

 

к единице свидетельствует о сильной зависимости между признаками. При небольшом

числе наблюдений (

n m

20 ) величина множественного коэффициента корреляции, как

 

m

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

правило, завышается. В этом случае множественный коэффициент корреляции корректируется:

 

 

 

 

 

R y / x1 ,x2 ,...,xm

1 (1 R2 )

n 1

,

 

 

n m 1

 

 

 

 

(7.10)

80

где R — скорректированное значение; n — число наблюдений;

m — число факторных признаков.

Корректировка R не производится при условии, если

n m m

20

.

Проверка значимости множественного коэффициента корреляции осуществляется по критерию Фишера:

 

 

 

1

R

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

m

y / x

,x

,...,x

 

 

F

 

 

 

 

 

1

2

m

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

pac

 

1

 

 

 

 

R

 

 

 

 

 

 

 

1

 

 

 

 

n m 1

 

 

 

2

 

 

 

 

 

 

y / x

,x

,...x

 

 

 

 

 

 

 

 

 

1

2

m

.

(7.11)

Множественный коэффициент

Fpac Fq (v1 m, v2 n m 1) . Здесь

корреляции

считается

значимым,

если

q – уровень значимости.

 

 

7.2 Вычисление непараметрических коэффициентов корреляции

Если признаки подчиняются различным (отличным от нормального) законам распределения, то можно рассчитать непараметрические коэффициенты корреляции. Эти коэффициенты могут быть использованы для определения тесноты связи как между количественными, так и между качественными признаками при условии, если их значения упорядочить или проранжировать по степени убывания или возрастания признака.

Среди непараметрических методов оценки тесноты связи наибольшее распространение получили следующие:

1. Коэффициент ранговой корреляции Спирмана:

 

 

 

 

 

n

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

1

6 di

,

 

 

 

i 1

 

 

 

 

 

 

 

 

 

 

 

x / y

 

n(n

2

1)

 

 

 

 

 

 

 

 

где d 2

– квадрат разности рангов;

 

 

 

 

 

i

 

 

 

 

 

 

 

n

— число наблюдений (число пар рангов).

 

(7.12)

Коэффициент Спирмана проверяется на основе определяется по формуле:

принимает значения от -1 t -критерия Стьюдента.

до 1. Значимость коэффициента

Расчетное значение

t -критерия

t

 

 

 

n 2

pac

x / y

1

2

 

 

 

 

 

 

x / y

 

 

 

 

 

Значение коэффициента корреляции

считается

tpac t (v n 2).

.

статистически существенным, если

2.Коэффициент ранговой корреляции Кендалла

 

2(P Q)

 

2S

,

(7.13)

n(n 1)

n(n 1)

 

 

 

 

где n — число наблюдений;

S — разность между числом последовательностей и числом инверсий по второму признаку. Расчет коэффициента Кендалла производится в такой последовательности:

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности