Приборы и устройства оптического и СВЧ диапазонов

371

ЗДЕЛ ЧЕТВЕРТЫЙ

ОПТОЭЛЕКТРОННЫЕ СИСТЕМЫ И ИХ ПРИМЕНЕНИЯ

Глава 16. Системы обработки и хранения информации

Эффективная и своевременная обработка больших массивов информации является одной из важнейших научно-технических проблем. Развитие науки и техники идет по пути необычайно быстрого и постоянно увеличивающегося роста потока информации, подлежащего переработке и использованию. Появление большого количества задач, решение которых целиком зависит от возможности переработки больших массивов информации, выдвигают высокие требования к своевременной и эффективной ее обработке.

В данной главе мы рассмотрим возможности применения оптико – электронных устройств в области обработки и хранения информации. В основу изложения этой главы взяты материалы из [44-48].

Любой физический процесс, несущий в себе ту или иную информацию, называется сигналом. В оптике носителем информации является световая волна. Следовательно, световая волна может рассматриваться как оптический сигнал. Преобразование таких сигналов производит оптический процессор.

Чем больший объем информации может быть закодирован в параметрах носителя информации, чем больше скорость его прохождения через систему обработки, тем больше быстродействие такого устройства. Использование когерентного светового поля (лазерного излучения) в качестве переносчика информации позволяет создать достаточно гибкую систему обработки информации, способную обрабатывать большой объем данных в очень короткое время.

Оптические системы в большинстве случаев представляют собой специализированные процессоры для выполнения основных математических операций, одно- и двумерного преобразований Фурье, вычисления корреляционных функций. Такие системы высокоэффективны и обладают большим быстродействием. На базе таких систем могут быть построены гибкие оптические процессоры, способные решать широкий класс радиотехнических задач.

16.1. Структура системы оптической обработки сигналов

Сейчас имеется много оптических и цифровых процессоров, которые при высокой скорости обработки данных (до миллиарда операций умножения и сложения в секунду) обеспечивают высокую точность измерения параметров выходных сигналов. Одним из перспективных направлений применения оптических методов является обработка радиолокационных сигналов. Быстродействие радиолокационных станций (РЛС) с системой оптической обработки информации (1012...1014 бит/с) значительно превышает быстродействие РЛС с традиционной электронной обрабатывающей системой (106...108 бит/с).

372

Структурная схема системы оптической обработки сигналов приведена на рис. 16.1.Для выполнения заданного алгоритма обработки на аналоговое оптическое вычислительное устройство поступают оптические сигналы, в которых закодирована информация, выдаваемая источником информации. Преобразование электрических сигналов в оптические выполняется источником света и преобразователем входных сигналов в оптический аналог. После выполнения заданного алгоритма обработки аналоговое оптическое вычислительное устройство формирует на выходе системы распределения амплитуд и фаз света, в которых содержатся результаты обработки сигналов, поступающих от источника инфор-

Рис. 16.1. Структурная схема системы оптической обработки сигналов.

мации. Преобразователь выходных сигналов измеряет параметры световых сигналов, поступающих на его выход, и выдает получателю информации конечный результат обработки в необходимом виде (как правило, в виде электрических сигналов). Преобразователь входных сигналов является устройством ввода информации в оптическую обрабатывающую систему, поэтому требования к нему во многом зависят от тех требований, которые предъявляются к системе обработки информации. Так например, при обработке оптической системы, предназначенной для обработки сигналов, поступающих на антенную решетку, требования к устройству ввода будут определяться характеристиками РЛС: дальностью обнаружения, разрешающей способностью системы по направлению, полосой пропусканию, динамическим диапазоном обрабатываемых сигналов, быстродействием. Таким образом, устройство ввода должно быть многоканальным (50 - 100 каналов), иметь высокую чувствительность, широкую полосу пропусканию (десятки МГц), идентичные характеристики отдельных каналов, низкий уровень собственных шумов, большой динамический диапазон обрабатываемых сигналов (не менее 40 дБ). В качестве устройств ввода применяются различные типы про- странственно-временных модуляторов света, принцип работы которых основан на взаимодействии света с динамическими неоднородностями, реализуемыми различными физическими эффектами в твердых и жидких веществах.

Оптические методы обработки информации. В решении проблемы эффек-

тивной обработки больших массивов информации особый интерес представляют оптические методы. Это обусловлено исключительно высокой информационной емкостью светового поля как переносчика информации, высокой скоростью распространения оптических сигналов и легкостью осуществления целого ряда интегральных операций над двумерными массивами информации. Потенциальные возможности оптических методов обработки информации позволяют надеяться в будущем на существенный прогресс в развитии вычислительной техники.

373

Наряду с применением оптических и оптоэлектронных элементов в средствах дискретной счетно-решающей техники в последние годы интенсивно развиваются аналоговые оптические методы и средства обработки информации, в основе которых лежат явления переноса информации пространственномодулированным волновым полем и дифракции света.

В отличие от оптоэлектронных устройств ЦВМ, где параллельная обработка информации может осуществляться за счет пространственной дискретизации, в аналоговых оптических вычислительных устройствах она реализуется естественным образом при эквивалентном числе каналов, определяемом разрешающей способностью оптической системы и используемого носителя информации. Так, например, при размере обрабатываемого транспаранта 24х24 мм, записанного на носителе с разрешающей способностью 100 мм-1 (легко реализуемый случай), эквивалентное число параллельных каналов составит 5,76×106.

Эффективность обработки информации с помощью оптических методов можно проиллюстрировать на примере осуществления преобразования Фурье. Как известно, операция двумерного Фурье-преобразования над когерентным оптическим сигналом осуществляется обыкновенной сферической линзой за время, равное времени распространения света в оптической системе, т. е. за 10-9 сек. при оптической длине анализатора в 30 см. Если учесть, что в 1 см2 носителя может содержаться до 109 бит информации (при разрешающей способности носителя 3000 мм-1), то потенциальная производительность такого аналогового оптического анализатора составит 1018 бит/сек.×см2. Это на много порядков превышает производительность самых совершенных ЭЦВМ.

На практике скорость обработки информации ограничивается скоростью ввода и вывода информации, а не временем обработки оптических сигналов. Однако и с учетом ограничений быстродействия, связанных с вводом и выводом информации, аналоговые оптические вычислительные устройства все же оказываются намного более производительными, чем ЭЦВМ (приблизительно на 4 порядка).

Аналоговая оптическая обработка информации может быть реализована с помощью как когерентных, так и некогерентных световых полей. Аналоговые оптические вычислители, использующие некогерентный свет, непосредственно оперируют с интенсивностью светового поля, а фазовая модуляция в таких системах может быть осуществлена только косвенным образом. Они конструктивно просты, но решают сравнительно узкий круг задач, связанных с обработкой главным образом одномерных сигналов (спектральный и корреляционный анализ и некоторые другие операции). Когерентные оптические системы обработки информации оперируют с амплитудами и фазами светового поля. Эти системы более гибкие и позволяют решать широкий круг задач по обработке двумерных комплексных функций, задаваемых в виде некоторого распределения амплитуд и фаз светового поля. Однако они конструктивно сложнее, чувствительны к механическим воздействиям и предъявляют более жесткие требования к качеству оптических элементов, пространственно-временным модуляторам (управляемым транспарантам) и источникам света. Следует отметить, что почти все математические операции над оптическими сигналами, реализуемые в когерентном свете, могут быть выполнены и в некогерентном свете, однако степень сложности практической

374

реализации будет зависеть от вида операции, т. е. решаемой задачи. Так, например, операция двумерного Фурье-преобразования в когерентном свете реализуется исключительно просто, а в некогерентном свете необходимо использовать серию масок, число которых зависит от требуемой точности выполнения операции.

16.1.1. Принцип аналоговой оптической обработки информации с помощью когерентных световых полей

Интерес к применению оптических методов в аналоговой вычислительной технике обусловлен тем фактом, что любая оптическая система по своей природе является аналоговым устройством обработки информации, поступающей на ее вход в виде светового поля, модулированного в пространстве и во времени.

Обобщенная структурная схема аналоговой когерентной оптической системы обработки информации приведена на рис. 16.2 и включает в себя оптический квантовый генератор ОКГ, расширитель пучка 7, устройство ввода информации 2, аналоговое оптическое вычислительное устройство 3, устройство вывода информации 4, запоминающее устройство 5.

Устройство ввода осуществляет пространственную модуляцию сформированной расширителем пучка плоской монохроматической волны по амплитуде, фазе или поляризации в соответствии с обрабатываемыми сигналами, поступающими на его вход. Основной задачей устройства ввода является преобразование подлежащих обработке сигналов в когерентные оптические сигналы (поля). Обрабатываемые сигналы могут иметь различную физическую природу, однако обычно они преобразуются либо в электрические, либо в оптические. В первом случае устройство ввода должно иметь электронный вход и оптический выход, а во втором — оптический вход и оптический выход.

Аналоговое оптическое вычислительное устройство осуществляет над сформированным когерентным оптическим сигналом требуемую математическую операцию. Результат обработки в общем случае представляет собой некоторую световую картину. Устройство вывода преобразует результат вычисления в электрический сигнал для трансляции в ЭЦВМ (или иное электронное устройство) или регистрирует на светочувствительный носитель (например, фотопленку).

Когерентные аналоговые оптические вычислительные устройства позволяют относительно просто выполнять следующие математические операции над функциями двух переменных: умножение, интегрирование, сложение и вычитание, преобразование Фурье, свертку, взаимную корреляцию, дифференцирование, преобразования Гильберта, Френеля и др.

Перечисленные операции могут быть реализованы различными способами. Обычно используют разного рода маски, с помощью которых осуществляют пространственную модуляцию поля по требуемому закону, или голограммы. Запоминающее устройство (оптическое или голографическое) служит для хранения требуемого набора эталонных масок или голограмм и является обязательным элементом оптико-электронных информационно-поисковых систем и многофункциональных аналоговых оптических вычислительных устройств.

375

Рис. 16.2. Структурная схема аналоговой оптической системы обработки информации

Можно показать, что даже на основе двух базовых операций — умножения и преобразования Фурье, которые проще всего реализуются в оптике, возможно выполнить широкий класс операций по обработке информации: операцию свертки, дифференцирование, интегрирование с весом, преобразования Френеля, изменение масштаба аргумента функции, восстановление функции из ее спектральной плотности, сложение и вычитание и другие.

Когерентные аналоговые оптические вычислители обладают следующими основными достоинствами.

1. Обеспечивают возможность параллельной обработки больших массивов информации благодаря своей двухмерности и чрезвычайно высокой информационной емкости светового поля и используемого носителя.

2. Обеспечивают высокую скорость выполнения операций, не зависящую от степени их сложности, которая практически ограничивается скоростью ввода— вывода информации, а не скоростью собственно обработки, определяемой временем прохождения света от входа до выхода системы.

Хотя в целом аналоговые оптические вычислители уступают ЦВМ по точности вычисления, однако, благодаря быстроте вычислений, простоте аппаратуры и ее обслуживания, отсутствию необходимости программирования они оказываются более эффективными при решении ряда практических задач. Чаще всего эти задачи связаны с выполнением операций спектрального и корреляционного анализа над двумерными комплексными функциями. Решение их на ЭЦВМ сопряжено со значительными затратами машинного времени и потому не всегда экономически оправдано. В некоторых частных случаях оптические методы обработки не уступают электронным по точности и даже превосходят их.

Следует отметить, что в значительной части задач обработки информации эвристического типа не требуется высокой абсолютной точности промежуточных вычислений. В частности, в задачах опознавания изображений, где оптическими методами осуществляется формирование корреляционного поля анализируемых изображений, важна не абсолютная точность вычислений кросскорреляционных функций, а обеспечение требуемого относительного превышения максимума сигнала опознавания над фоном.

Оптические методы обработки информации, несмотря на их еще короткую историю развития, находят уже достаточно широкое применение в вычислительной технике, кибернетике, радиотехнике, радиолокации и связи, экспериментальной физике, астрономии, метеорологии и геофизике, машиностроении и приборо

376

строении, криминалистике, микроэлектронике, медицине, биологии, биофизике и др.

В настоящее время развитие методов и средств оптической обработки информации идет по пути создания специализированных аналоговых оптических вычислительных устройств для решения широкого круга прикладных задач, связанных в большинстве случаев с необходимостью осуществления спектрального или корреляционного анализа над двумерными массивами информации, а также пространственной фильтрации.

Оптические устройства обработки информации можно классифицировать по ряду различных признаков: области применений, назначению решаемых задач, виду обрабатываемых сигналов и т.д. Можно условно объединить, существующие устройства оптической обработки информации, в следующие четыре группы осуществляющие: 1) спектральные анализ; 2) пространственную фильтрацию; 3) корреляционный анализ; 4) интегральные преобразования (Гильберта, Френеля и др.).

16.2. Способы выполнения математических операций оптическими системами

Оптическое умножение. В оптической системе обработки информации сигналы обычно перемножаются путем модуляции светового потока объектом, устанавливаемом в плоскости изображений (транспарантом). Функция пропускания транспаранта T(x,y) известна и умножается на входной сигнал, заданный в виде распределения амплитуд и фаз светового потока. Предположим, что в фокальной плоскости Р1 (рис. 16.3,а) расположен транспарант с коэффициентом прозрачности

пределение амплитуды светового поля можно записать в следующем виде (см.

рис. 16.3, б):

Как видно, выражение (5.2) описывает операцию умножения постоянной величины A(x1,y1)=const функцию T1(x1,y1) . Если вплотную к транспаранту поставить другой транспарант с функцией пропускания T2(x1,y1), то на выходе получим результат перемножения в виде

Следовательно, суммарная модуляционная характеристика транспаранта, полученного при наложении нескольких транспарантов, равна произведению модуляционных характеристик отдельных транспарантов (экранов), а носителем информации являются световая волна. Таким образом, в оптическом решающем устройстве сигналы перемножаются путем модуляции светового потока с помощью оптических элементов (экранов, транспарантов, линз, решеток и т.п.), амплитудное пропускание которых соответствует перемножаемым сигналам, Оптическое умножение и более комплексных функций можно осуществить с помощью оптической системы, показанной на рис. 16.4.

Рис. 16.4 Оптическое умножение комплексных функций

378

Сложение сигналов. В оптическом решающем устройстве световое поле в любой точке пространства есть результат суммирования световых полей, приходящих в эту точку. При этом вычисляется сумма, т.е. учитываются амплитуды и фазы поля. Если требуется строго определенное соотношение фаз отдельных сигналов при их суммировании, то возникает сложная задача контроля фазовых сдвигов сигналов. В свою очередь величина фазового сдвига сигнала зависит от длины оптического пути, пройденного сигналом. Так как длина волны света, например, λ = 0,63 мкм, то изменение пути всего на несколько долей микрометра приводит к существенному изменению фазовых сдвигов сигналов. В качестве примера на рис. 16.5 показано, как складываются спектрах двух сигналов. В передней фокальной плоскости линзы расположен экран с записью сигналов S1(x,y) и S2(x,y), соответственно на верхней и нижней половинах экрана. В задней фокальной плоскости линзы световой поток Eo , прошедший экран, собирается, образуя сумму спектров входных сигналов. На практике устанавливаются весьма высокие требования к точности взаимного расположения сигналов.

По условию λ /Tx<<I , точность (Tx= 1/fx ; fx - пространственная частота сигнала) установки сигнала в передней фокальной плоскости должна быть порядка минимального периода пространственной частоте сигнала. На практике сложение сигналов находит достаточно широкое применение и является одной из основных операций при обработке информации.

Интегрирование. Операция интегрирование выполняется линзой, в фокусе которой амплитуда и фаза соответствуют интегралу от функции распределения света в плоскости изображений линзы:

В общем случае можно утверждать, что если линза выполняет преобразование Фурье над сигналом S(x,y) ,то в точке (ω x = 0,ω y = 0 ) выходного сигнала вы-

полняется операция интегрирования сигнала. Интегрирование такого рода есть вычисление постоянной составляющей сигнала. Операцию интегрирования легко

379

реализовать с помощью элементарной оптической системы, если сделать равными единице экспоненциальный множитель в преобразований Фурье, выполняемом той системой. Это означает, что надо приравнять нулю переменные x1 и y1. Практически это можно сделать с помощью точечной диафрагмы или оптического приемника малого размера, который должен располагаться точно на оптической оси (рис. 16.6а). В одномерных многоканальных

системах используется щелевая диафрагма, причем направление щели совпадает с линией фокусов цилиндрической линзы (рис. 16.6, б).

Дифференцирование функций. Дифференцирование функций осуществляется в частотной области, т.е. в области преобразования Фурье. Применяя теорему о спектре производной временного сигнала, для n-ой производной можно получить выражение

из которого следует, что первая производная функции определяется произведением спектра S(ω ) на угловую частоту ( ω ).

Для пространственных сигналов это означает, что в плоскости преобразования Фурье необходимо поставить фильтр, состоящий из маски с нулевой прозрачностью в центре и постепенно увеличивающейся прозрачностью к краям, (т.е. по мере возрастания пространственной частоты), а так же полуволновой пластинки, осуществляющей сдвиг фазы (перемену знака) для отрицательных пространственных частот.

16.2.1. Вычисление корреляционных функций

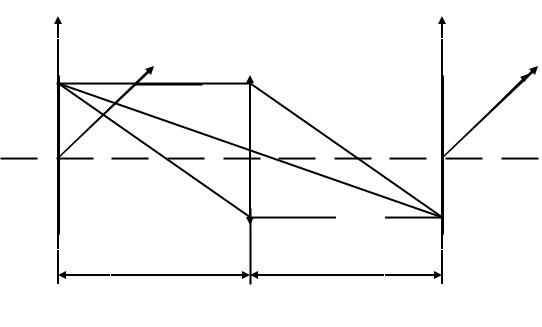
Рассмотрим оптическую систему, изображенную на рис. 5.7. Цилиндрическая линза z1 выполняет преобразование Фурье по оси х в плоскости (ω x , y) , а

линза z2 - проектирует изображение сигнала S(x,y) по оси y на ту же плоскость. По оси y(ω х=0) распределение светового поля соответствует одномерно-

380

где q(x1-xo,y) – функция пропускания дополнительного экрана в плоскости (х,у),

входной диафрагмы), можно обеспечивать различные интегральные операции. Линия взаимное положение экранов (переменная xo ), на оси у выходной плоскости можно получить взаимно корреляционную функцию сигналов S(x) , и q(x) в различных каналах по оси у.

Если тот же экран с функцией пропускания (q(x1-xo,y1)) повернуть, наложив его на экран c функцией пропускания, будет равно зеркальному отображению q(x1-xo) , т.е. q(xo-x1 ) . Такая система выполняет операцию свертки сигналов S(x) и q(x). Но такие оптические системы обладают следующими недостатками; необходимость относительного перемещения сигналов, вычисление интеграла последовательно во времени в процессе перемещения сигналов.

16.2.2. Преобразование

Фурье в оптической системе

Разберем, как элементарная оптическая система, схема которой дана на рис. 16.8, может быть описана математически [48]. Если представим источник U , расположенный на плоскости Рi , в виде бесконечно малой δ величины и запишем его величину освещенности в виде соотно-