Микроволновые приборы и устройства

141

кинетической энергии электронов в электромагнитную энергию. Говоря об электрическом поле волны, мы будем иметь в виду осевую составляющую Еz, выделяя тормозящий и ускоряющийr движение электронов полупериоды (рис. 6.2). Вектор Е направлен от заряда к Ө.

Рассмотрим механизм взаимодействия электронов с бегущей волной.

Пусть по спирали движется бегущая волна со скоростью υф. В тех участках спирали, где мгновенное направление поля Ez совпадает с направлением скорости электронов υ0 , поле для электронов тормозящее, а там, где направление Ez противоположно направлению υ0 , поле ускоряет электроны (рис. 6.2).

Рис. 6.2 — Тормозящее и ускоряющее электрическое поле в спирали

Если поле волны уменьшает скорость электронов, то энергия волны будет увеличиваться. Если электроны вводятся в участки волны, увеличивающие скорость, то энергия их возрастает, а волны — уменьшается. Обмен энергиями отсутствует, если электроны попали в участки, где в данный момент нет электронного поля.

Для работы ЛБВ нужно сосредоточить возможно большее количество электронов в тормозящих участках поля и меньшее — в ускоряющих. Электронная пушка посылает равномерный поток электронов. Поэтому в тормозящих и ускоряющих участках в начале ЗС оказывается одинаковое количество электронов. Благодаря задаваемой разнице в скоростях волны и потока происходит группирование электронов в тормозящем поле. Поясним это.

Построим графики движения электронов относительно некоторой точки z0 , движущейся по оси спирали со скоростью υф

(рис. 6.3).

142

Рис. 6.3 — Графики смещения электронов относительно волны при разных соотношениях скоростей

Предположим, что электроны, не взаимодействуют с волной и перемещаются вдоль оси с начальной скоростью υ0 . Тогда в за-

висимости от отношения υ0 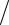υф графики движения электронов изображаются в виде прямых линий. Если υ0 = υф, электрон в любой момент времени t находится против точки z0 (график 1). Если υ0 < υф, то с течением времени электрон будет отставать от наблюдателя, движущегося со скоростью υф (график 2). При υ0 > υф электрон постепенно опережает точку z0 (график 3).

На рис. 6.4 изображены графики движения электронов, взаимодействующих с бегущей волной. Период колебаний разбит на восемь промежутков. На этих графиках выбрано несколько точек наблюдения, соответствующих разным моментам прихода электронов к началу спирали. Так, например, точка z2 на рис. 6.4,

а соответствует электрону, который влетел в спираль в момент, когда поле было максимально ускоряющим; точка z1 — другому

электрону, попавшему в спираль, когда Ez меньше максимальной

величины. Пунктиром обозначено движение электронов в отсутствии высокочастотного поля. На рис. 6.4, а показаны графики движения электронов для случая υ0 = υф. Электроны, попавшие в

ускоряющее поле, движутся все быстрее и постепенно опережают точку наблюдения, электроны, попавшие в тормозящее поле, теряют скорость и отстают. В результате электроны группируются в сгустки, симметричные относительно точки Ez = 0. На рис. 6.4,

143

б, в показаны графики движения электронов при υ0 < υф и υ0 > υф. В случае υ0 < υф сгустки электронов образуются в об-

ласти ускоряющего высокочастотного поля. В процессе дальнейшего движения электроны отбирают энергию у поля, и амплитуда волны уменьшается. Соотношение υ0 < υф является не-

рабочим. В случае υ0 > υф электроны группируются в тормозящем поле волны.

а б в

Рис. 6.4 — Графики движения электронов под действием поля бегущей волны, причем z = (v0 −vф)t . Сплошные линии — с учётом взаимодействия

с волной, пунктирные — без учёта

Дальнейшее их движение сопровождается потерей скорости и, следовательно, передачей энергии от электронного потока волне. Соотношение между скоростями в виде υ0 >υф характерно для

рабочего режима лампы.

6.2Взаимодействия поля волны с электронами

в«горячем» режиме ЛБВО (линейное приближение)

Исходные предпосылки

Рассмотрим взаимодействие волны и потока в условиях υ0 > υф. В результате рассмотрения должна быть найдена величи-

на постоянной распространения волны Г& в ЗС в горячем режиме в функции от режима питания U0 , Io , ω и параметра — Rсв.

145

ведут к тому, что плотность его начнет изменяться и из непрерывного потока он преобразуется в модулированный по плотности. Необходимо определить величину переменной составляющей конвекционного тока. Для этого воспользуемся уравнениями движения, тока переноса и непрерывности

Из уравнения (6.2) определим скорость:

dυ(z,t) = ∂υ + ∂υ dz = iωυ1eiωt−Гz − Г&υ1eiωt−Гz (υ0 + υ1eiωt−Гz ), от- dt ∂t ∂z dt

куда

где учтено, что произведение υ1υ1 = 0, как малые 2-го порядка. Подставим в (6.2) выражение (6.5) и Ez = Emzeiωt−Гz :

m(iωυ1 − Гυ1υ0 )eiωt−Гz = −eEmzeiωt−Гz .

Откуда

Соотношение (6.6) дает величину переменной составляющей скорости электронов в пучке, возникшую под действием амплитуды поля Emz .

Найдем переменную составляющую плотности конвекцион-

Из выражения плотности тока переноса (6.3) и допущений получим

146

Получена амплитуда переменной составляющей конвекционного тока пучка, возникшая в результате воздействия ВЧ-поля Ezm в ЗС.

Переменное напряжение на ЗС, наводимое конвекционным током

Сгустки электронов, двигающиеся вдоль ЗС, наводят по ней ВЧ-токи, которые на сопротивлении связи создают переменное напряжение, добавляющееся к токам и напряжению, созданным только бегущей по ЗС волной, в результате чего изменяется и поле Ezm бегущей волны. Для определения этого изменения ис-

пользуем метод эквивалентных схем. Составим эквивалентную схему замещения ЗС (рис. 6.5), на которой ЗС будет представлена однородной линией без потерь с идеальными (без потерь) зазорами; ВЧ-напряжение — U будет соответствовать продольному

147

напряжению ЗС на уровне электронного потока; фазовая скорость волны υф реальной ЗС и эквивалентной пусть одинаковы, а

характеристическое сопротивление эквивалентной схемы равно сопротивлению связи Rсв.

Рис. 6.5 — Эквивалентная схема замещения ЗС

Для элемента линии длиной dz при погонном сопротивлении iX0 и при погонной проводимости iB0 дифференциальные

dI = −UiB0dz + dIk , где dIk — приращение конвекционного тока пучка, или dUdz = −IiX0 , dIdz = −UiB0 + dIdzk , из которых определяем

U . Учтем (6.1)

здесь неизвестны X0 , B0 — параметры холодной лампы, которые следует исключить. Для этого в (6.11) и (6.12) положим Ik = 0 и

148

Рис. 6.6 — Эквивалентная схема элемента линии длиной dz

Подставим (6.14) в (6.13) и получим величину напряжения, создаваемого на ЗС модулированным по плотности конвекционным током Ik = I1 в луче; обратное действие этого напряжения на

здесь величины Г и Г0 не известны.

Характеристическое уравнение ЛБВО позволяет опреде-

лить постоянную распространения Г в горячем режиме и получается при одновременном решении уравнений (6.9) и (6.15). В уравнении (6.15) подставим (6.1) и Ezm , представив в виде

Ezm = − dUdz = −gradU = ГU1 .

Тогда характеристическое уравнение для Г принимает вид:

Учитывая допущения, упростим (6.16).

149

Скорости волны и потока соотносятся υф ≤ υ0 , поэтому по-

стоянная распространения Г в присутствии луча не должна сильно отличаться от постоянной распространения в холодной лампе Г0 . Решаем (6.16) при близких значениях Г, Г0 , iKэ. Электрон-

ное волновое число Kэл = ω равно постоянной холодной лампы,

υ0

т.е. Г0 = jKэл .

При наличии электронного потока (горячий режим), допустим, Г = Г0 + ξ незначительно отличается от Г0 на ξ — малую

величину. Подставим Г и Г0 в (6.16), преобразуем его, получим упрощенное характеристическое уравнение

−Rc I0 K(эл2 (−Kэл2))=1; 2U0 −2ξ3iKэл

где С = 3 RcвI0 — безразмерный параметр усиления. 4U0

Решение характеристического уравнения (6.17а). Запи-

шем его в виде

где использовано обозначение 3 i = δ.

Если найдем δ, то сможем записать величину Г в виде

cos3φ+isin3φ = i .

Приравниваем действительные и мнимые части в последнем равенстве

(6.19)

Из соотношений (6.19) следует, что по ЗС в присутствии электронного потока и принятых допущений распространяются 3 волны, имеющие одинаковую структуру поля, но разные постоянные распространения. Фазовые постоянные распространения определяют фазовые скорости υф1 , υф2 , υф3 .