Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Томский Государственный Университет Систем Управления и Радиоэлектроники

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Математическое и имитационное моделирование экономических процессов в MATHCAD..pdf

Скачиваний:

Добавлен:

05.02.2023

Размер:

6.12 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 1920 / 2520 21 22 23 24 25 > Следующая >>>

		108
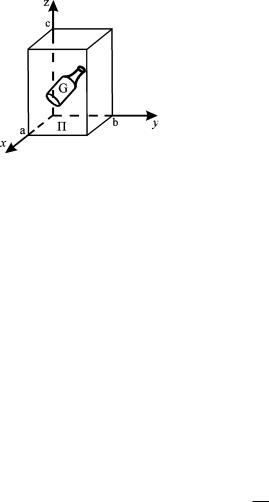
	Возьмем		прямоугольный		параллелепипед		,
	содержащий область			G . Объем параллелепипеда П
	известен и равен V a b c . Разыграем координаты N
	случайных точек, равномерно распределенных в
	области , и обозначим через				NG количество точек,
	попавших в		область	G. При	большом	N	будет
Рис. 9.1	приближенно выполняться соотношение
	приближенно выполняться соотношение
			NG / N VG /V ,
из которого найдем
			VG V NG / N .				(9.2)
В нашем примере случайная величина
	V		, G,


			G,
	0,		G,

а среднее арифметическое равно

1	N	G

	i		V (NG / N ) .
N
	i 1

(9.3)

При решении задач ММК необходимо генерировать случайные величины равномерно распределенные в интервале [0; 1].

9.2. Оценка точности результатов, полученных методом

Монте-Карло

Оценка точности результатов, полученных методом Монте-Карло, основана на центральной предельной теореме теории вероятностей, из которой следует, что

при большом объеме выборки N относительная частота события	A	сходится по
	A

вероятности к вероятности события pA , а среднее арифметическое выборочных данных сходится по вероятности к их математическому ожиданию. Используя ММК, можно провести большое число независимых опытов и с заданной точностью найти оценки искомых величин. При расчетах ММК возникает вопрос оценки точности полученных результатов. Ответ на этот вопрос можно получить на основе центральной предельной теоремы, из которой следует, что при

109

большом объеме выборки плотность вероятности выборочного среднего приближается к нормальному распределению.

Пусть производится большое число N независимых опытов, в каждом из

которых событие

появляется с вероятностью

p	A

. Введем СВ

1,	если	A,

X	если	A,
0,	если	A,

Оценка вероятности p

события

определяется формулой

i 1

(9.4)

где N A число опытов, в которых появилось событие

. Отношение

NA / N

определяет относительную частоту события

. Распределение

при большом

значении N близко к нормальному с математическим ожиданием

m ( p

) p

среднеквадратическим отклонением

( p	A	)
	A

p	A	(1 p	A	)
	A		A
		N

(9.5)

Если СВ вид

является непрерывной, то оценка математического ожидания имеет

	N
	i
	x
mx	i 1	,	(9.6)
mx	N	,	(9.6)
	N

где xi выборочные данные. Оценка (1.8) при большом значении N является приближенно нормальной СВ со средним M mx M X и

среднеквадратическим отклонением

(mx )	x	N
	x

Рассмотрим два примера по определению точности результатов расчетов, полученных ММК.

			110
Пример 1. Проведено N независимых опытов, в каждом из которых событие				A
появляется с некоторой неизвестной нам вероятностью p . В результате этих
ˆ
опытов получена оценка pA по формуле (3.4). Найти вероятность P pA pA
ˆ
того, что pA отличается от вероятности pA не больше чем на заданную
величину 0 . Так как оценка	p	A	– при большом N нормальная СВ с
		A
математическим ожиданием pA	и среднеквадратическим отклонением (3.5), то
искомая вероятность равна

P pA pA					N
	2							.

		p		(1	p		)
			A			A

Здесь

(9.7)

	1	x	t	2
		x	t
(x)		e	2		dt
(x)		e			dt

	2	0
		0

(9.8)

функция Лапласа. Как пользоваться формулой (3.7), если вероятность	pA	нам
неизвестна и мы ее находим? В выражение (3.7) pA нужно заменить на	p A .

Задавая достаточно большую величину вероятности, например, равную 0,95,

0,98, можно найти необходимое значение			N для достижения заданной
точности.
Пример 2. Проведено N независимых опытов, в каждом из которых
наблюдается значение СВ	X	. Вычисляется оценка среднего значения mx						по
	X
формуле (3.6). Найти вероятность P mx mx того, что оценка mx
отклоняется от математического ожидания mx					не больше чем на заданную
величину 0 . Как и в предыдущем примере
P mx mx					2	N	,	(9.9)

		2				x
		(mx )				x
где x – среднеквадратичное отклонение СВ				X. Если величина x неизвестна,

то вместо нее можно использовать соответствующую оценку

111

		1	N	2
	x	1	xi mx	2	.	(9.10)
	x	N 1	xi mx		.	(9.10)
		N 1	i1
			i1
	Обычно на практике точность характеризуют величиной относительной
среднеквадратической ошибки x			mx , которая уменьшается с ростом			N	как
1	N .

9.3.Лабораторное задание

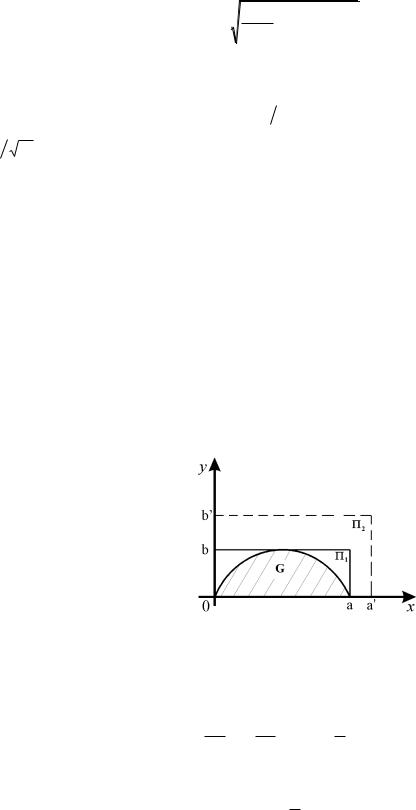
1.Разработать алгоритм вычисления площади заданной фигуры методом

Монте-Карло и написать для него программу в пакете Mathcad. Определить величину относительной средне-квадратичной ошибки вычисленной оценки для

различных прямоугольных областей	, содержащих заданную фигуру
G (см. рис. 9.2). Найти точное значение площади заданной фигуры и сравнить
полученные результаты.

Рис. 9.2

Фигура задана следующей кривой

y(x)

Площадь фигуры равна S

y(x)dx

ab .

Значения параметров a, a и b,b

приведены в таблице 9.1.

(9.11)

№	1	2	3	4	5	6	7	8	9	10
варианта

a b a b

				112
2	3	4	5	6	5	4	3	2	1
4	5	6	7	8	9	10	9	8	7
3	3	5	5	7	7	6	6	4	4
5	5	6	8	8	10	10	10	10	10

2. Разработать алгоритм вычисления объёма заданной фигуры методом МонтеКарло и написать для него для него программу в пакете Mathcad. Определить величину относительной средне-квадратичной ошибки вычисленной оценки для различных прямоугольных областей , содержащих заданную фигуру

G (см. рис. 1.3). Найти точное значение объема заданной фигуры и сравнить полученные результаты.

Фигура представляет собой прямоугольный параллелепипед с размерами a b h , срезанный сверху параболоидом вращения

	x	2	y	2
		2		2
y(x, y) h		2	p	.
		2	p

Вершина параболоида совпадает с центром верхнего основания.

(9.12)

Объём фигуры равен

	a / 2	b / 2
V			z(x, y)dxdy abh
	a / 2 b / 2

ab	(a	2

24 p

b	2	)

Значения параметров

p, h

a,b

a ,b , h

приведены в таблице 9.2.

№	1	2	3	4	5	6	7	8	9	10
варианта

1	1,5	2	2,5	3	4	0,5	0,1	1	2
10	12	15	18	11	13	8	9	6	7
1	2	3	4	5	5	2	1	2	1
4	5	5	6	5	6	1	0,5	2	5
2	3	4	5	6	6	3	2	3	2

b h

			113
5	6	6	7	6	7	2	1	3	6
11	13	16	20	12	15	10	10	7	8

Указания. Для вычисления объема VG (площади SG ) заданной геометрической фигуры G необходимо разыграть координаты N случайных точек с равномерным распределением в прямоугольной области . Тогда оценки

величины объема (площади ˆ ) можно вычислить по формулам:

V G SG

где

– число точек,

V G a b h N		G	/

SG a b N	G	/ N

попавших в область G .

Если в математическом пакете отсутствует равномерный датчик случайных

чисел из интервала [ p; q], то значение СВ	z с равномерной плотностью
вероятности в заданном интервале [ p; q] можно получить с помощью линейного
преобразования

		z p x (q p) ,	(9.13)
где	x	обозначает СВ с равномерной плотностью вероятности в интервале [0;

1]. Величину относительной среднеквадратической погрешности оценок объема

V G (площади S G ) можно вычислить по формуле:

	N NG	.

	NNG

Контрольные вопросы

1. Что можно сказать о точности результатов, полученных методом численного моделирования, и как они зависят от объема выборки?

114
2. Определите величину интервала ,	в котором находится найденная оценка

площади (объема) заданной фигуры с вероятностью 0,9. Значения функции Лапласа приведены в таблице 9.3.

	1	x		t	2
		x		t
Таблица 9.3. Значения функции Лапласа (x)			e	2		dt	[2]
				2
	2

		0
		0

0,00

0,01

0,02

0,03

0,04

0,05

0,06

0,07

0,08

0,09

0,10

0,11

0,12

0,13

0,14

0,15

0,16

0,17

0,18

0,19

(x)

0,0000

0,0040

0,0080

0,0120

0,0160

0,0199

0,0239

0,0279

0,0319

0,0359

0,0398

0,0438

0,0478

0,0517

0,0557

O,O596

0,0636

0,0675

0,0714

0,0753

0,31

0,32

0,33

0,34

0,35

0,36

0,37

0,38

0,39

0,40

0,41

0,42

0,43

0,44

0,45

0,46

0,47

0,48

0,49

0,50

(x)

0,1217

0,1255

0,1293

0,1331

0,1368

0,1406

0,1443

0,1480

0,1517

0,1554

0,1591

0,1628

0,1664

0,1700

0,1736

0,1772

0,1808

0,1844

0,1879

0,1915

0,62

0,63

0,64

0,65

0,66

0,67

0,68

0,69

0,70

0,71

0,72

0,73

0,74

0,75

0,76

0,77

0,78

0,79

0,80

0,81

(x)

0,2324

0,2357

0,2389

0,2422

0,2454

0,2486

0,2517

0,2549

0,2580

0,2611

0,2642

0,2673

0,2703

0,2734

0,2764

0,2794

0,2823

0,2852

0,2881

0,2910

0,93

0,94

0,95

0,96

0,97

0,98

0,99

1,00

1,01

1 02

1 04

1,04

1,05

1,06

1,07

1,08

1,09

1,10

1,11

1,12

(x)

0,3238

0,3264

0,3289

0,3315

0,3340

0,3365

0,3389

0,3413

0 3438

0,3461

0 3485

0,3508

0,3531

0,3554

0,3577

0,3599

0,3621

0,3643

0,3665

0,3686

				115
0,20		0,51	0,1950		0,82	0,2939	1,13	0,3708
0,20	0,0793	0,51	0,1950		0,82	0,2939	1,13	0,3708
0,21	0,0832	0,52	0,1985		0,83	0,2967	1,14	0,3729
0,22	0,0871	0,53	0,2019		0,84	0,2995	1,15	0,3749
0,23	0,0910	0,54	0,2054		0,85	0,3023	1,16	0,3770
0,24	0,0948	0,55	0,2088		0,86	0,3051	1 17	0,3790
0,25	0,0987	0,56	0,2123		0,87	0,3078	1,18	0,3810
0,26	0,1026	0,57	0,2157		0,88	0,3106	1,19	0,3830
0,27	0,1064	0,58	0,2190		0,89	0,3133	1,20	0,3849
0,28	0,1103	0,59	0,2224		0,90	0,3159	1,21	0,3869
0,29	0,1141	0,60	0,2257		0,91	0,3186	1,22	0,3883
0,30	0,1179	0,61	0,2291		0,92	0,3212	1,23	0,3907

Продолжение приложения

x	(x)	x
x	(x)	x
1,24		1,58
1,24	0,3925	1,58
1,25	0,3944	1,59
1,26	0,3962	1,60
1 27	0,3980	1,61
1,28	0,3997	1,62
1,29	0,4015	1,63
1,30	0,4032	1,64
1,31	0,4049	1,65
1,32	0,4066	1,66
1,33	0,4082	1,67
1,34	0 4099	1,68
1,35	0,4115	1,69

(x)

0,4429

0,4441

0,4452

0,4463

0,4474

0,4484

0,4495

0,4505

0,4515

0,4525

0,4535

0,4545

1,92

1,93

1,94

1,95

1,96

1,97

1,98

1,99

2,00

2,02

2,04

2,06

(x)

0,4726

0,4732

0,4738

0,4744

0,4750

0,4756

0,4761

0,4767

0,4772

0,4783

0,4793

0,4803

2,52

2,54

2,56

2,58

2,60

2,62

2,64

2,66

2,68

2,70

2,72

2,74

(x)

0,4941

0,4945

0,4948

0,4951

0,4953

0,4956

0,4959

0,4961

0,4963

0,4965

0,4967

0,4969

				116
1,36		1,70	0,4554		2,08	0,4812	2,76	0,4971
1,36	0,4131	1,70	0,4554		2,08	0,4812	2,76	0,4971
1,37	0,4147	1,71	0,4564		2,10	0,4821	2,78	0,4973
1,38	0,4162	1,72	0,4573		2,12	0,4830	2,80	0,4974
1,39	0,4177	1,73	0,4582		2,14	0,4838	2,82	0,4976
1,40	0,4192	1,74	0,4591		2,16	0,4846	2,84	0,4977
1,41	0,4207	1,75	0,4599		2,18	0,4854	2,86	0,4979
1,42	0,4222	1,76	0,4608		2,20	0,4861	2,88	0,4980
1,43	0,4236	1,77	0,4616		2,22	0,4868	2,90	0,4981
1,44	0,4251	1,78	0,4625		2,24	0,4875	2,92	0,4982
1,45	0,4265	1,79	0,4633		2,26	0,4881	2,94	0,4984
1,46	0,4279	1,80	0,4641		2,28	0,4887	2,96	0,4985
1,47	0,4292	1,81	0,4649		2,30	0,4893	2,98	0,4986
1,48	0,4306	1,82	0,4656		2,32	0,4898	3,00	0,49865
1,49	0,4319	1,83	0,4664		2,34	0,4904	3,20	0,49931
1,50	0,4332	1,84	0,4671		2,36	0,4909	3,40	0,49966
1,51	0,4345	1,85	0,4678		2,38	0,4913	3,60	0,499841
1,52	0,4357	1,86	0,4686		2,40	0,4918	3,80	0,499928
1,53	0,4370	1,87	0,4693		2,42	0,4922	4,00	0,499968
1,54	0,4382	1,88	0,4699		2,44	0,4927	4,50	0,499997
1,55	0,4394	1,89	0,4706		2,46	0,4931	5,00	0,499997
1,56	0,4406	1,90	0,4713		2,48	0,4934
1,57	0,4418	1,91	0,4719		2,50	0,4938

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 1920 / 2520 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
05.02.20232.17 Mб11Математические основы теории систем.-2.pdf
#
05.02.20232.18 Mб10Математические основы теории систем..pdf
#
05.02.2023974.28 Кб6Математический Аппарат Теории Сигналов и Систем.-1.pdf
#
05.02.2023435.96 Кб3Математический аппарат цифровой микроэлектроники..pdf
#
05.02.20235.2 Mб11Математическое и имитационное моделирование экономических процессов в Mathcad.-1.pdf
#
05.02.20236.12 Mб20Математическое и имитационное моделирование экономических процессов в MATHCAD..pdf
#
05.02.2023198.97 Кб2Математическое и имитационное моделирование экономических процессов.-1.pdf
#
05.02.2023582.34 Кб7Математическое и имитационное моделирование экономических процессов.-2.pdf
#
05.02.20232.32 Mб12Математическое и имитационное моделирование экономических процессов.-3.pdf
#
05.02.20235.16 Mб27Математическое и имитационное моделирование экономических процессов..pdf
#
05.02.20233.3 Mб5Математическое и компьютерное моделирование объектов и систем управления..pdf

1	1,5	2	2,5	3	4	0,5	0,1	1	2
10	12	15	18	11	13	8	9	6	7
1	2	3	4	5	5	2	1	2	1
4	5	5	6	5	6	1	0,5	2	5
2	3	4	5	6	6	3	2	3	2

1	1,5	2	2,5	3	4	0,5	0,1	1	2
10	12	15	18	11	13	8	9	6	7
1	2	3	4	5	5	2	1	2	1
4	5	5	6	5	6	1	0,5	2	5
2	3	4	5	6	6	3	2	3	2

1	1,5	2	2,5	3	4	0,5	0,1	1	2
10	12	15	18	11	13	8	9	6	7
1	2	3	4	5	5	2	1	2	1
4	5	5	6	5	6	1	0,5	2	5
2	3	4	5	6	6	3	2	3	2