
Теоретические основы электротехники. Часть 1. Установившиеся режимы в линейных электрических цепях
.pdf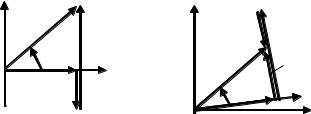
ными составляющими емкости bC = ω C и проводимости
b |
L |
|
1 |
. Если b |
|
|
b |
|
, то |
0 , и входная проводи- |
|
|
|
||||||||||
|
|||||||||||
|
|
L |
C |
|
|
L |
|
|
2 |
||
|
|
|
|
|
|
|
|
|
мость цепи имеет резистивно-емкостный характер (рис. 2.8, а). Векторная диаграмма для токов и напряжений (рис. 2.8, б) соответствует случаю, когда φ > 0.
Im |
Y |
Im |
IL |
IC |
|
|
|||
|
|
YC |
|
|
|
>0 |
|
|
IL+IC |
|
|
|
I |
|
|
|
|
|
|
YR |
YL |
Re |
>0 |
U |
|
|
|
||
|
|
|
IR |
Re |
|
а) |
|
|
б) |
|
|
Рис. 2.8. |
|
|
Уравнения, описывающие процессы в параллельной RLC- цепи, подобны по структуре уравнениям для последовательной RLC-цепи и могут быть получены одно из другого путем замены тока на напряжение, проводимости – на сопротивление, емкости – на индуктивность. Следовательно, параллельная и последовательная RLC-цепи являются дуальными.
2.5. Активная, реактивная, полная и комплексная мощности
Активная мощность определяется как среднее значение мгновенной мощности за период и численно равна
P = U I cos φ. (2.22)
По знаку активной мощности можно судить о направлении передачи энергии. При P > 0 двухполюсник потребляет энергию, при P < 0 – отдает энергию остальной части цепи.
Полной мощностью S называется величина, равная произведению действующих значений тока и напряжения на входе цепи
S = U I. |
(2.23) |
41
Активная мощность цепи может быть выражена через полную мощность:
P = S cos φ. |
(2.24) |
Таким образом, полная мощность есть максимальное значение активной мощности при φ = 0.
Комплексное число S, модуль которого равен полной мощности цепи S, а аргумент – углу сдвига фаз между током
и напряжением φ, называется комплексной мощностью цепи:
S = S ejφ.
Переходя от показательной формы записи к тригономет-
рической |
|
S = S cos φ + jS sin φ, |
(2.25) |
устанавливаем, что вещественная часть комплексной мощности равна активной мощности цепи:
Re(S) = S cos φ = P;
мнимая часть S представляет собой реактивную мощность цепи:
Im(S) = S cos φ = Q. |
(2.26) |
Реактивная мощность характеризует процессы обмена энергией между цепью и источником. Мощность, запасаемая в магнитном поле цепи, больше нуля, а запасаемая в электрическом поле – меньше нуля.
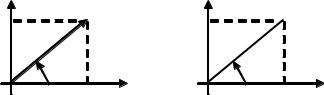
Комплексному числу S соответствует вектор S, проекции которого на вещественную и мнимую оси равны соответственно P и Q (рис. 2.9, а). Прямоугольный треугольник, катетами которого являются P и Q, а гипотенузой – S, называется треугольником мощностей. Очевидно, что активная, реактивная и полная мощности связаны соотношением S2 = P2 + Q2, вследствие чего треугольник мощностей подобен треугольнику сопротивлений этой же цепи (рис. 2.9, б), и компоненты мощности S (S, P, и Q) могут быть выражены через сопротивление Z и его компоненты Z, R и X:
2 |
|
|
R 2 |
(2.27) |
|
S U I I Z; P S cos U I |
|
I R; |
|||
Z |
|
||||
Q Ssin U I |
X |
I 2 X ; S S e j I 2Z e j I 2 Z. |
|
||
Z |
|
||||
|
|
|
|
|
|
42
|
Im |
S |
|
Im |
Z |
Q |
|
X |
|
||
|
|
|
|
||
|
S |
|
|
Z |
|
0 |
|
|
0 |
|
|
|
|
|
|
||
|
|
P Re |
|
|
R Re |
|
|
а) |
|
|
б) |
Рис. 2.9.
Связь между комплексной мощностью и комплексными действующими значениями тока и напряжения задается соотношением
|
|
U e j u I e j i , |
|
|
S U I |
(2.28) |
|
|
I e j i – комплексно сопряженный ток. |
|
|
где I |
|
||
2.6. Баланс мощностей
Рассмотрим электрическую цепь, содержащую N идеальных источников напряжения, M идеальных источников тока и H идеализированных пассивных элементов. Тогда уравне-
ние баланса мгновенных мощностей
N M |
H |
|
pk и |
pk п , |
(2.29) |
k 1 |
k 1 |
|
где pkи – мощность источника, pkп – мощность потребителя. Уравнение баланса комплексных мощностей удобно за-
писать в форме
|
N |
|
|
M |
|
|
|
|
H |
|
|
|
S И E k I k |
|
U |
k J k |
I k2 Z k |
S П . |
|||||||
|
||||||||||||
|
k 1 |
|
|
k 1 |
|
|
|
|
|
k 1 |
|
|
Отсюда следует баланс активных мощностей |
||||||||||||
N |
|
|
|
M |
|
|
|
|
H |
2 |
||
PИ Re E k I k |
Re U k |
J k |
I k Rk PП , |
|||||||||
k 1 |
|
|
|
k 1 |
|
|
|
|
k 1 |
|
||
баланс реактивных мощностей |
|
|
2 |
|
||||||||
|
|
|
|
|
|
|
||||||
N |
|
|
|
M |
|
|
|
|
|
|
H |
|
QИ Im E k I k Im |
U |
k |
J k I k |
X k QП , |
||||||||
k 1 |
|
|
|
k 1 |
|
|
|
k 1 |
|
|||
cos φ = P/S называется коэффициентом мощности.
(2.30)
(2.31)
(2.32)
(2.33)
43
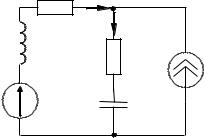
Пример 2.5. В цепи (рис. 2.10) напряжения на соответ-
ствующих индексам элементах и ток I1 |
имеют следующие |
||||||||||||
значения: |
|
|
|
|
|
|
|
|
UR1 = 2,33 ej149,8º В; |
||||
|
|
|
|
|
|
|
|
|
|
|
UR2 = 6,93 ej210,5º В; |
||
|
|
R1 |
|
I1 |
I2 |
|
|
|
|
|
j239,8º |
В; |
|
|
|
|
|
|
|
|
|
|
|
UL = 4,66 e |
|||
L |
|
|
|
|
R2 |
|
J |
|
UC = 0,77 ej120,5º В; |
||||
|
|
|
|
|
|
|
UJ = 6,97 ej24,2º В; |
||||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
I1 = 2,33 ej144,8º В. |
||
|
E |
|
|
|
|
C |
Проверить |
выполнение ба- |
|||||
|
|
|
|
|
|
|
|
|
ланса мощностей. |
|
|||
|
|
|
Рис. 2.10 |
|
|
|
|
Решение. В соответствии с |
|||||
|
|
|
|
|
условием баланса мощностей |
||||||||
|
|
|
|
|
|
|
|
|
|||||
мощность источников равна мощности потребителей: Sи = Sп. |
|||||||||||||
|
|
|
|
|
|
|
|
21,5 j9,06 10 3 В А; |
|
|
|||
Sи E I1 |
U J J |
|
|
|
|||||||||
S |
п |
I 2 |
R j X |
L |
I 2 |
R j X |
C |
21,4 j9,07 10 3 В А. |
|||||
|
1 |
|
1 |
|
|
2 |
2 |
|
|
|
|||
Условие баланса выполняется.
2.7. Преобразования электрических цепей
Понятие об эквивалентных преобразованиях. Анализ процессов в электрических цепях может быть существенно упрощен за счет использования различных преобразований, в результате которых отдельные участки цепей заменяются эквивалентными – либо с более простой топологией, либо более удобными для анализа.
Два участка цепи называются эквивалентными, если при замене одного из этих участков другим токи и напряжения в остальной части цепи не изменятся. Преобразования такого типа также называются эквивалентными. Отметим, что преобразуемые электрические цепи должны иметь одинаковое число внешних выводов, и в процессе преобразований токи выводов и напряжения между ними должны оставаться неизменными.
Рассмотрим правила преобразования цепей с последовательным и параллельным соединениями.
44
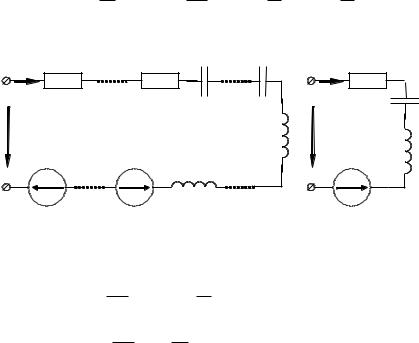
Участки цепи с последовательным соединением эле-
ментов. Рассмотрим одноконтурную цепь (рис. 2.11). Уравнение этой цепи составим по второму закону Кирхгофа для мгновенных значений:
|
1 |
|
|
|
1 |
|
di |
di |
|
|
R1i Rn i C1 |
i dt Cm |
i dt |
L1 dt |
Lk dt |
|
(2.34) |
||||
|
|
|
u e1 e p . |
|
|
|
||||
i |
R1 |
|
|
R n |
C1 |
|
C m |
i |
Rэ |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
C1 |
u |
|
|
|
|
|
|
L1 |
u |
|
|
|
e p |
|
e1 |
|
|
|
eэ |
|
Lэ |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
Lk |
|
|
|
|
|
|
а) |
|
|
|
|
|
|
б) |
|
|
|
|
|
|
|
Рис. 2.11. |
|
|
|
||
|
После приведения подобных (2.34) примет вид: |
|
|
|||||||
|
|
1 |
|
di |
|
|
|
|
|
|
|
RЭ i C |
Э |
i dt LЭ dt |
u |
eЭ , |
|
|
(2.35) |
||
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
m |
|
|
k |
p |
|
|
где RЭ Ri ; |
|
1 |
1 ; LЭ |
Li ; |
eЭ ei . |
|
|
|||
|
i 1 |
CЭ |
i 1 |
Ci |
|
i 1 |
i 1 |
|
|
|
Если обобщенная одноконтурная цепь находится под гармоническим воздействием, то от эквивалентной схемы (рис. 2.11) удобнее перейти к электрической схеме для комплексных значений (рис. 2.12, а). Уравнения (2.34) в комплексной форме в этом случае имеют вид:
Z R1 I Z R n I Z C 1 I Z C m I Z L1 I Z L k I
|
U E1 E p . |
(2.36) |
|
|
|
||
После преобразований получаем ZЭ I = U – EЭ, |
|||
n |
m |
k |
p |
где Z Э Z R i Z C i Z L i ; EЭ Ei . |
|||
i 1 |
i 1 |
i 1 |
i 1 |
45
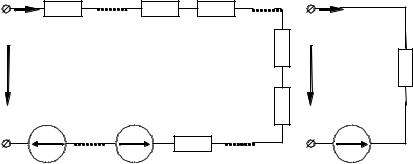
Эквивалентная цепь для комплексных действующих значений приведена на рис. 2.12, б.
I |
ZR1 |
ZRn |
ZC1 |
I |
|
|
|
|
|
||
|
|
|
|
ZCm |
|
U |
|
|
|
U |
Zэ |
|
Ep |
E1 |
|
ZL1 |
Eэ |
|
ZLk |
|
|||
|
|
|
|
|
|
|
|
а) |
|
б) |
|
Рис. 2.12.
Участки цепи с параллельным соединением элемен-
тов. Пусть электрическая цепь (рис. 2.13, а) состоит из параллельно соединенных n активных сопротивлений, m емкостей, k индуктивностей и p независимых источников тока (обобщенная двухузловая цепь). Все элементы цепи находятся под одним и тем же напряжением u, поэтому уравнение цепи, по первому закону Кирхгофа
|
i |
|
1 |
|
u |
1 |
|
|
u C |
du |
C |
|
du |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
m dt |
||||||||||||||||
|
|
|
|
|
|
R |
|
|
|
|
|
R |
n |
|
|
|
1 |
dt |
|
(2.37) |
||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
1 |
|
|
u dt |
|
1 |
|
|
u dt J J . |
|||||||||||||||
|
|
|
L |
|
|
L |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
p |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
||
После приведения подобных |
|
|
|
|
||||||||||||||||||||||||
i |
1 |
|
|
u |
CЭ |
du |
|
|
|
1 |
|
u dt J Э , |
|
|
(2.38) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
R |
|
|
|
|
dt |
|
|
L |
|
|
|
||||||||||||||||
|
|
|
Э |
|
|
|
|
|
|
|
|
|
|
Э |
|
|
|
|
|
|
|
|
||||||
n
где RЭ Ri ;
i 1
Уравнению
(рис. 2.13, б).
1 |
k |
1 |
|
m |
p |
|
|
; CЭ |
Ci ; J |
Э Ji . |
|||
L |
L |
|||||
i 1 |
|
i 1 |
i 1 |
|||
Э |
i |
|
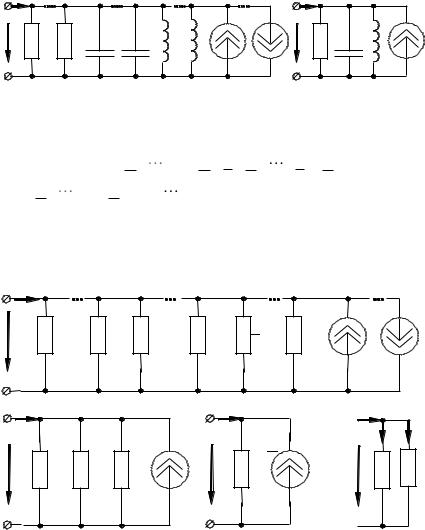
(2.38) соответствует преобразованная цепь
46
i |
|
|
|
|
|
|
J1 |
Jp |
i |
|
Jэ |
|
|
|
|
|
|
|
|
||||
u |
R1 |
|
R n |
C1 |
Cm |
|
|
|
u |
Rэ Cэ |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
L1 |
Lk |
|
|
|
Lэ |
|
|
|
а) |
|
|
|
|
|
|
б) |
|
|
|
|
|
|
|
|
Рис. 2.13. |
|
|
|
|
|
При гармоническом воздействии для комплексной схемы |
||||||||||
замещения (рис. 2.14, а, б, в) |
|
|
|
|
|||||||
|
|
|
I Y R1U |
Y RnU Y C1U |
Y C mU |
|
|||||
Y L1U |
Y Lk U J 1 |
J p . |
|
|
|
|
|||||
|
После преобразований: |
|
|
|
|
||||||
|
|
|
|
|
I Y Э U J Э , |
|
|
|
(2.39) |
||
|
|
|
n |
|
m |
|
k |
|
p |
|
|
где Y Э |
Y R i Y C i |
Y L i ; |
J Э |
J i . |
|
|
|||||
|
|
|
i 1 |
i 1 |
|
i 1 |
|
i 1 |
|
|
|
I |
|
|
|
|
|
|
|
|
|
J1 |
Jp |
|
|
|
|
|
|
|
|
|
|
||
U |
|
YR1 |
YR n |
YC1 |
YC m |
YL1 |
YLk |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
а)
I |
Jэ |
I |
Jэ |
I |
I1 I2 |
|
|
U |
|
||
U |
YRэ YCэ YLэ |
U |
Yэ |
|
|
|
|
|
|
Z1 |
Z2 |
|
б) |
|
в) |
г) |
|
Рис. 2.14.
Используя формулу преобразования цепей с параллельным соединением элементов, получаем правило растекания токов в параллельных пассивных ветвях (не содержащих источников энергии) (рис. 2.14, г)
47

Y |
1 |
; |
Z |
|
|
Z1 Z2 |
; |
U I Z |
|
; |
I |
U |
|
I |
|
Z2 |
. |
|||||||||||
|
Э |
|
|
|
|
|||||||||||||||||||||||
|
|
|
Z |
|
|
Э |
|
Z Z |
2 |
|
|
|
|
|
|
|
1 |
Z |
|
|
|
Z Z |
2 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
||||
То есть ток ветви равен подтекающему току, умноженному на сопротивление смежной ветви и деленному на сумму сопротивлений этих ветвей.
Эквивалентные преобразования треугольника сопротивлений в звезду и звезды – в треугольник. Такие преобра-
зования должны быть эквивалентными по отношению к внешней цепи. Это значит, что подходящие к выводам токи должны быть одинаковы, одинаковы также должны быть напряжения между выводами, т.е. I 1 , I 2 , I 3 и U 12 , U 2 3 , U 31 одинаковы как для звезды (рис. 2.15, а), так и для треугольника (рис. 2.15, б) сопротивлений.
Соотношения эквивалентности для комплексных значений при переходе от треугольника к звезде:
Z 1 |
|
|
Z 12 Z |
31 |
; |
Z 2 |
|
|
Z 12 Z |
23 |
; |
Z 3 |
Z 23 |
Z 31 |
. (2.40) |
|
Z 12 |
Z 2 3 |
Z 31 |
Z 12 |
Z 23 |
Z 31 |
Z12 Z |
2 3 Z 31 |
|||||||||
|
|
|
|
|
|
|
|
При переходе от звезды к треугольнику:
Z |
|
Z |
|
Z |
|
|
Z1 Z 2 |
; Z |
|
Z |
|
Z |
|
|
Z 2 Z 3 |
; Z |
|
Z |
|
Z |
|
|
Z 3 Z1 |
. (2.41) |
|
12 |
1 |
2 |
Z 3 |
23 |
2 |
3 |
Z1 |
31 |
3 |
1 |
Z 2 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Выражения комплексных проводимостей, образующих стороны треугольника, могут быть получены из (2.41) путем замены комплексных сопротивлений их проводимостями:
Y 12 |
|
Y 1Y 2 |
; Y 2 3 |
|
Y 2 Y 3 |
; |
Y 31 |
|
Y 3 Y 1 |
. |
|
Y 2 Y 3 |
Y 2 Y 3 |
Y 2 Y 3 |
|||||||||
|
Y 1 |
|
Y 1 |
|
|
Y 1 |
|
||||
|
|
|
|
|
Пример |
2.6. |
Рассчитать |
||||
|
|
|
|
|
комплексное входное сопро- |
||||||
|
R1 |
C1 |
L1 |
|
тивление |
цепи (рис. 2.16) с |
|||||
|
|
|
|
|
параметрами: |
|
|
||||
|
|
C2 |
R2 |
|
R1 R2 |
1кОм ; |
|
|
|||
|
|
|
С1 С2 |
0,5 нФ ; |
|
||||||
|
|
|
|
|
|
||||||
|
|
Рис. 2.16. |
|
|
L 10 мГн ; |
f 39,8 кГц . |
|
||||
|
|
|
|
|
|
|
|
|
|
||
48
Решение. Эквивалентное комплексное сопротивление
ветви с элементами R1, C1, L1 ZЭ1 = ZR1 + ZC1 + ZL1. Комплексное сопротивление параллельно включенных
ветвей с ZЭ1 и C2
Z Э2 |
Z Э1 Z C 2 |
. |
|
||
|
Z Э1 Z C 2 |
|
Комплексное входное сопротивление цепи ZВХ = ZR2 + ZЭ2. Подставив значения параметров элементов цепи в выражения
Z R1 Z R2 R1 , Z L j L , Z C1 Z C 2 |
j |
, |
|
|
|||
C1 |
|||
получим: ZВХ = 1 кОм. |
|
||
|
|
2.8. Расчет электрических цепей со взаимной индуктивностью
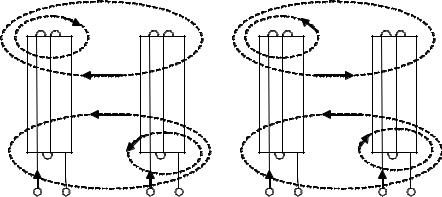
Понятие взаимной индуктивности. Две или несколько катушек индуктивности называются связанными, если изменение тока в одной из них приводит к появлению ЭДС в остальных (рис. 2.17).
Полный магнитный поток первой и второй катушек соответственно:
Ф1 Ф11 Ф12 ; Ф 2 |
Ф 2 2 Ф 21 . |
(2.42) |
Согласное включение |
Встречное включение |
|
|
Ф11 |
|
|
|
|
Ф11 |
|
|
Ф21 |
|
|
|
|
Ф21 |
|
|
Ф12 |
|
|
|
|
Ф12 |
|
|
Ф22 |
|
|
|
|
Ф22 |
|
i1 |
i2 |
|
|
i1 |
|
i2 |
|
|
|
|
|
|
|
||
1 |
1' |
2 |
2' |
1 |
1' |
2 |
2' |
|
а) |
|
|
|
|
б) |
|
|
|
|
Рис. 2.17. |
|
|
|
|
|
|
|
|
|
|
|
49 |

Так как правомерна связь:
1 N1Ф1 N1Ф11 N1Ф12 ; 2 N2Ф 2 N2Ф 2 2 N2Ф 21 , (2.43)
где Ψ1 и Ψ2 – потокосцепления катушек, то, учитывая фор-
мулу e |
d |
, запишем: |
|
|
|
|
|
|
|
|
|
|
|
||||||
dt |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
d |
11 |
|
d |
12 |
|
|
|
d |
2 2 |
|
d |
21 |
|
|
|||
e |
|
|
|
|
|
|
; e |
|
|
|
|
|
. |
(2.44) |
|||||
|
|
|
|
|
2 |
|
|
|
|
||||||||||
1 |
|
|
dt |
dt |
|
|
|
dt |
dt |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|||||||||||
Знак «+» соответствует совпадающим по направлению магнитным потокам самоиндукции и взаимоиндукции, и такое включение называется согласным (рис. 2.17, а). Знак «–» соответствует противоположным направлениям этих потоков, и такое включение называется встречным (рис. 2.17, б).
Запишем выражение (2.44) относительно напряжений в комплексной форме:
U1 |
= jω(L1 I1 ± M12 |
I2); |
(2.45) |
U2 = jω(L2 I2 ± M21 I1).
Здесь M12 = M21 =M – взаимная индуктивность катушек L1 и L2, равная M kС В 
 L1L2 ; kС В – коэффициент связи, не пре-
L1L2 ; kС В – коэффициент связи, не пре-
вышающий 1.
Полная комплексная мощность катушек, обусловленная взаимной индуктивностью,
|
j 2 M I 1 I 2 |
|
^ |
|
|
|
|
||
S M |
cos I 1 I 2 |
. |
||
|
|
|
|
|
Здесь знак «+» соответствует согласному включению, знак «–» – встречному.
Введем понятие одноименных зажимов. При одинаковых направлениях токов относительно одноименных зажимов двух индуктивно связанных катушек магнитные потоки самоиндукции и взаимоиндукции складываются. В противном случае зажимы называются разноименными.
Эквивалентные преобразования участков цепей со свя-
занными индуктивностями. Рассмотрим эквивалентные преобразования участков цепей со взаимоиндуктивностями и
50
