
Электродинамика и распространение радиоволн
..pdf





поскольку разность хода r согласно равенству (12.16) не зависит от r, а только от угла θ.
Для дальнейшего анализа рассмотрим случай слабонаправленных антенн (F(θ1) ≈ F(θ2 )), когда интерференционный множитель представляется формулой (12.11). Заменим в ней угол θ1 на θ и h1 на h:
|
|
|
2 |
[ |
] |
(12.18) |
||
V (θ) = |
1+ |
R |
+ 2 |
R |
cos |
2khcos(θ) + Φ . |
||
В зависимости от поляризации поля передающей антенны рассмотрим два случая.
1. Горизонтальная поляризация. Примером таких антенн является горизонтальный вибратор. Пусть вначале Земля считается идеально проводящей (σ = ∞). Тогда согласно формулам (12.1) и (12.2) R =1, Φ = π и формула (12.18) приобретает вид
|
|
|
|
V (θ) = 2 |
|
sin (khcos(θ)) |
|
. |
(2.19) |
|||||||||||||
|
|
|
|
|
|
|||||||||||||||||
|
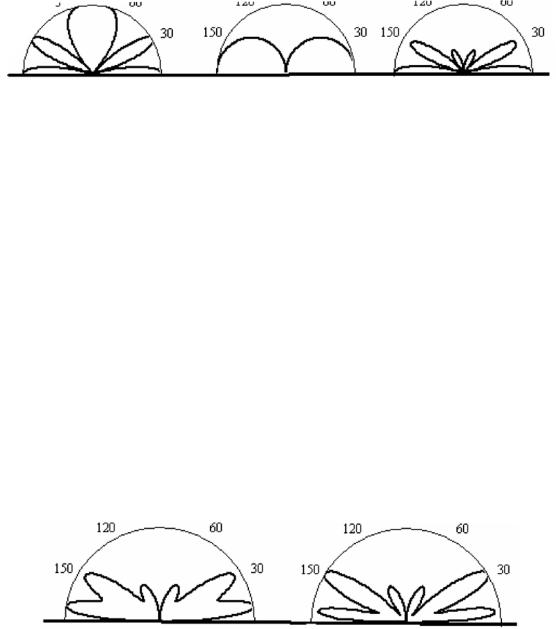
Поскольку диаграмма направленности самого вибратора в эк- |
|||||||||||||||||||||
ваториальной плоскости представляет |
окружность ( F(θ1)= 1), то |
|||||||||||||||||||||
F(θ) = V(θ), т.е. диаграмма направленности определяется только |
||||||||||||||||||||||
множителем Земли V(θ). Графики функции F(θ) представлены на |
||||||||||||||||||||||
рис. 12.6 для различных отношений h λ. |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
90° |
|
|
|
|
|
|
|
|
|
|
|
|
|
90° |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
120° |
|
||||||||
|
|
|
120° |
|
60° |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
60° |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
150° |
|
|
|
|
150° |
|
|
|
|
|
|
|
30° |
|
|||||||
|
|
|
|
30° |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||
а |
б |
Рис. 12.6. Диаграммы направленности горизонтального вибратора над идеально проводящей Землей: а – h λ=1; б – h
λ=1; б – h λ=2
λ=2
286






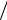
 2
2