Основы научно-исследовательской деятельности

В качестве примера использования численных методов может служить решение задачи виброформования бетонной смеси. Бетонная смесь при вибрации моделируется в виде сплошной упруговязкой среды, а математическая модель процесса виброформования представлена в виде

где – плотность бетонной смеси; t – время; x, y – декартовы координаты; vx – составляющая скорости бетонной смеси вдоль направления распространения колебаний; E – модуль упругости; l – смещение элемента бетонной смеси; – коэффициент динамической вязкости.

Первый член в правой части уравнения, описывающего процесс виброформования, представляет собой упругую составляющую среды, а второй – вязкую.

Решение полученного уравнения аналитическими методами является чрезвычайно сложным и обычно в литературе не приводится. Для практического использования оно может быть решено с использованием ЭВМ, для чего его необходимо представить в конечно-разностном (безразмерном) виде. Для этого введем следующие обозначения:

При численном интегрировании на ЭВМ это уравнение представляют в разностном виде, для чего производные заменяются конечно-разностными отношениями. Выбрав шаг x

по оси х и y по оси y, построим сетку xi = x0 + i x; yi = y0 + j y (i, j = 0, 1, 2, …) (рисунок 4.3). Тогда для первой производной функции f(x) получим следующие варианты записи:

где fi+1, fi, fi-1 – значения функции f в узлах интегрирования соответственно.

Значение функции в данном нулевом узле через шаг интегрирования по времени t обозначается через W0 t , где W0 – значение функции в нулевом узле в данный момент

времени. С учетом принятых обозначений модель виброформования бетонной массы примет вид

141

критерий подобия, представляющий отношение силы вязкостного трения к динамическому давлению.

Реализация предложенного алгоритма заключается в следующем. На основании последнего уравнения определяется безразмерное ускорение в заданном узле сетки интегрирования с использованием известных значений безразмерной скорости и перемещения в данный момент времени. Значения безразмерных перемещений и скорости в заданном узле сетки интегрирования в последующий момент времени определяется по формулам

Описанный процесс повторяется по всем узлам сетки интегрирования для данного момента времени. Это позволяет определять значения безразмерного ускорения для последующего момента времени по всем узлам сетки интегрирования.

Сучетом начальных условий u = –1, W = 0 и граничных, выраженных в виде uг = f1(t)

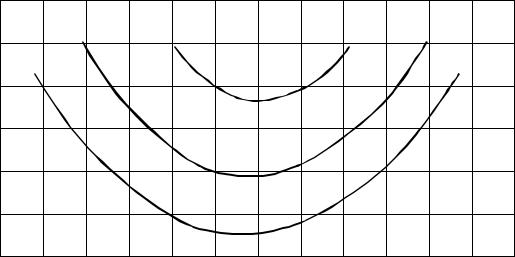
иWг = f2(t), можно последовательно получить численные значения скоростей и перемещений по всем узлам сетки интегрирования в функции координат и времени. Использование полученных значений u и W позволяет сравнительно просто определить напряженное состояние вибрируемой бетонной смеси (рисунок 5.9). Естественно, что вычисления в этом случае громоздки и необходимо использование специальных программ и ЭВМ.

Использование аналитических методов решения математических задач является основным методом современного научного исследования. Однако громоздкость моделей и прямых методов решения уравнений затрудняет получение конечных решений. Поэтому в решении практических задач нашли широкое применение методы преобразования

исходных уравнений (логарифмирование, преобразований Лапласа, Фурье и т.д.).

Логарифмирование уравнений является простейшим способом преобразований.

Пусть нам необходимо получить решение простейшего уравнения

y = a0.2,

которое называется оригиналом функции.

142

Возведение числа а в степень 0.2 прямыми методами затруднительно. Поэтому осуществляется преобразование данного уравнения при помощи логарифмирования

log y = 0.2log a

– это уравнение называется изображением функций.

При логарифмировании функция переводится из пространства оригиналов в пространство изображений и операция возведения в степень сводится к умножению чисел 0.2 и log a, что не встречает никаких затруднений.

При помощи антилогарифмирования полученный результат переводится из пространства изображений в пространство оригиналов.

Приведенный пример хорошо иллюстрирует и является аналогом преобразований Лапласа и преобразований Фурье.

Смысл указанных преобразований аналогичен логарифмированию. Например, в преобразованиях Лапласа исходная функция переводится из пространства оригиналов в пространство изображений при помощи интеграла

F ( p) f (t)e pt dt ,

0

Перевод функции из пространства изображений в пространство оригиналов осуществляется при помощи интеграла

Величина с выбирается так, чтобы обеспечить сходимость интеграла.

143

Преобразование Лапласа широко используется при решении дифференциальных и интегральных уравнений. В процессе решения этих уравнений широко используются таблицы преобразований функции, так же как это делается в случае логарифмирования.

Основываясь на методе преобразования функций, решаются задачи анализа переходных процессов в системах управления. В процессе анализа оперируют передаточными функциями.

Под передаточной функцией понимается отношение преобразования Лапласа выходной координаты линейной системы к преобразованию входной координаты при нулевых начальных условиях:

W ( p) y( p) , x( p)

где W(p) – передаточная функция; x(p) – преобразование Лапласа входного сигнала; y(p) – преобразование Лапласа выходного сигнала.

Вид передаточной функции может быть получен из дифференциального уравнения системы управления путем замены операции дифференцирования по времени оператором Лапласа p, а операции интегрирования по времени – заменой 1/p.

Например, если система управления описывается дифференциальным уравнением

то, произведя замену d на p и переходя к изображениям, получаем dt

py(p) + ay(p) = kx(p).

Такое представление дифференциального уравнения называется операционным.

Для нахождения передаточной функции этой системы достаточно произвести несложные алгебраические преобразования. В результате получим

Кроме метода передаточных функций для анализа систем управления широко используется метод частотных характеристик, который составляет теоретическую базу обобщенного гармонического анализа.

Под частотной характеристикой системы понимают отношение комплексных изображений выходной и входной амплитуд в установившемся режиме гармонических колебаний

W ( j ) A2 ( ) e j ( ) , A1

где A1 – амплитуда синусоидального входного сигнала; – круговая частота; А2( ) – амплитуда колебаний выходной координаты; ( ) – сдвиг по фазе синусоидальных колебаний выходной координаты.

Аналитически W(j ) можно получить из передаточной функции заменой параметра преобразования Лапласа p на j с последующим выделением модуля комплексного числа и фазового сдвига.

Частотные характеристики систем управления используют при анализе устойчивости, качества переходных процессов и динамической точности, синтеза корректирующих устройств.

Кроме перечисленных при решении задач широко используются: метод пространства состояний; метод компараментального анализа; информационные методы.

Рассмотрим примеры по составлению моделей.

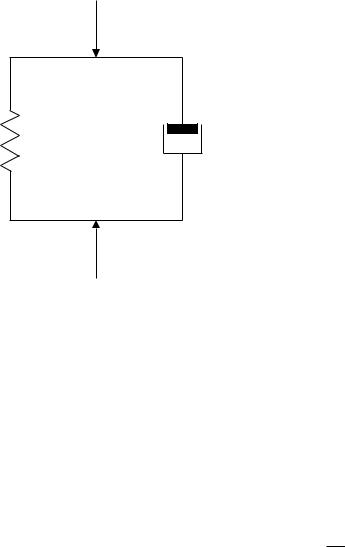
На рисунке 5.10 приведена модель деформирования. Модель 1, представленная пружиной, характеризует упругие свойства и подчиняется закону Гука – величина

144

деформации прямо пропорциональна прилагаемой нагрузке Р. Такой закон деформирования характерен для твердых упругих тел.

P

P

Рисунок 5.10 – Модель деформирования упруговязких материалов

Модель 2, представленная движением поршня в заполненном вязкой жидкостью цилиндре, характеризует вязкие свойства тел. Деформация тел в данном случае происходит медленно, развиваясь во времени, и подчиняется закону Ньютону – сопротивление пропорционально скорости демпфирования.

При параллельном соединении двух моделей в единое целое имеем модель деформирования упруговязкого тела. Такое деформирование подчиняется закону Кельвина.

Математическая модель, соответствующей физической модели (рисунок 5.10), может быть представлена в виде

где Py, PB – упругое сжатие пружины и вязкое сопротивление жидкости; Ey, Sy - модуль упругости и относительная деформация пружины; - коэффициент вязкости; dSdt - скорость

деформирования.

Решая (5.1) при t = 0, S = 0 , имеем

Зависимость (5.2) в ряде случаев хорошо согласуется с экспериментом и позволяет изучить законы деформирования упруговязких материалов.

Приведенный пример иллюстрирует процесс познания в соответствии с формулой – от живого созерцания (наблюдение за поведением материала) к абстрактному мышлению (физическая модель – рисунок 5.10 и уравнение (5.1)) и от него к практике – уравнение (5.2).

Рассмотренная модель соответствует функциональной зависимости, когда одному значению аргумента соответствует только одно значение функции. Однако в природе встречаются процессы, когда одному значению аргумента соответствует несколько значений функции вследствие действия на явление различных случайных факторов.

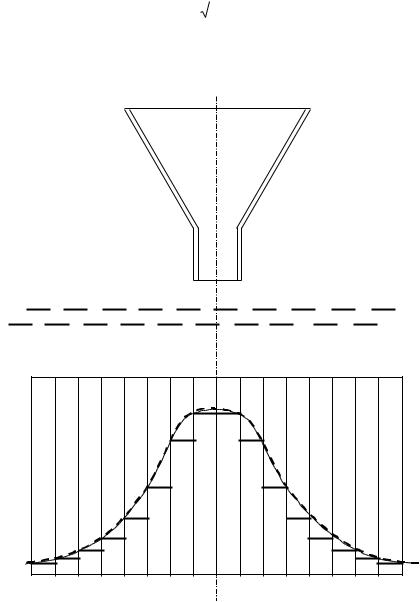
На рисунке 5.11 приведена физическая модель, характеризующая закон вероятностного распределения песка, который вытекает непрерывной струей из лейки через решето в ящик с вертикальными секциями. Наблюдения показывают, что распределение песка в ящике подчиняется закону нормального распределения:

145

где y – ордината, частота распределения песка или количество песка в секции; x - абсцисса, номер секции в ящике, отсчитываемой от середины; - среднеквадратическое отклонение.

Выражение (5.3) является математической моделью вероятностного процесса, приведенного на рисунке 5.11.

1

2

1 – воронка; 2 – решето; 3 – ящик с секциями

Рисунок 5.11 – Закономерность распределения песка

Широкое распространение получили модели, обеспечивающие оптимизацию технологических процессов и их управления. В связи с этим рассмотрим, так называемую,

транспортную задачу. Пусть имеется A1, A2, A3 объектов строительства, потребляющих соответственно a1, a2, a3 щебня (рисунок 5.12). В местах B1 и B2 есть притрассовые карьеры с

x11 + x12 + x13 = b1; x21 + x22 + x23 = b2.

А1

А2

В2

В1

А3

А – объекты строительства; В - карьеры

Рисунок 5.12 – Схема транспортных связей

В системе (5.4) первое уравнение означает количество щебня, транспортируемое из карьеров B1 и B2 на объект A1; второе – на объект A2. Последнее уравнение – количество щебня, доставляемое на объекты A1, A2, A3 из карьера B2, и т.д.

Все исходные данные сведены в матрицу условия задачи (таблица 5.1). Задача имеет много решений, так как есть шесть неизвестных в системе (5.4), состоящих из пяти уравнений. Требуется определить наиболее выгодный (экономичный) вариант перевозки щебня. В этом случае численными методами с помощью линейного программирования и ЭВМ находят функцию, которая удовлетворяет условию

147

5.4 Метод аналогии. Модели подобия

Явления, процессы изучаются не изолированно друг от друга, а комплексно. Различные объекты с их специфическими переменными величинами объединяются в комплексы, характеризуемые едиными законами. Это позволяет распространить анализ одного явления на другие или целый класс аналогичных явлений. При таком принципе исследований уменьшается число переменных величин, они заменяются обобщенными критериями. В результате упрощается искомое математическое выражение. На этом принципе основаны методы сочетания аналитических и экспериментальных исследований с методами аналогии, подобия, размерностей, являющихся разновидностью методов моделирования.

Суть метода аналогии рассмотрим на примере. Тепловой поток зависит от температурного перепада (закон Фурье):

T dx

Здесь – коэффициент теплопроводности. Массоперенос или перенос вещества (газа, пара, влаги) определяется перепадом концентрации вещества c (закон Фика):

- коэффициент массопереноса. Перенос электричества по проводнику с погонным сопротивлением обусловливается перепадом напряжения (закон Ома):

где – коэффициент электропроводности. Все три рассматриваемые явления характеризуются различными физическими процессами, но имеют идентичные математические выражения, т.е. их можно исследовать методом аналогий.

В зависимости от того, что принимается за оригинал и модель, могут быть различные виды моделирования методом аналогии. Так, если тепловой поток qT изучают на модели с движением жидкости, то моделирование называют гидравлическим; если тепловой поток исследуют на электрической модели, моделирование называют электрическим. Моделирование может быть механическим, акустическим и др. Целесообразность выбора вида моделирования зависит от сложности изучаемого процесса и модели, ее стоимости и эксплуатации, возможности постановки различных экспериментов, точности результатов.

Идентичность математических выражений процессов оригинала и модели не означает, что эти процессы абсолютно аналогичны. Для того чтобы на модели максимально моделировать изучаемый процесс оригинала, необходимо соблюдать критерий аналогий.

Так, сравнивать qT и qЭ, коэффициенты теплопроводности и электропроводности , температуру и напряжение u нет смысла. Для устранения этой несопоставимости оба уравнения необходимо представить в безразмерных величинах: каждую переменную величину ПП представить в виде произведения постоянной размерности на переменную

148