Квантовая и оптическая электроника

11

1.ПРЕДСТАВЛЕНИЕ ЭЛЕКТРОМАГНИТНОГО ИЗЛУЧЕНИЯ ОПТИЧЕСКОГО ДИАПАЗОНА

Использование когерентного светового поля (лазерного излучения) в качестве переносчика информации позволяет создать достаточно гибкую систему обработки информации, способную обрабатывать большой объем данных в очень короткое время. Лазерный луч, несущий информацию, можно представить в виде суммы плоских монохроматических волн с различными параметрами (амплитуды напряженности поля Ео; частоты изменения поля во времени ω ; начальной фазы колебаний ϕ о; вида поляризации; направления вращения поляризации; направления распространения волны).

Чем больший объем информации может быть закодирован в параметрах носителя информации, чем больше скорость его прохождения через систему обработки, тем больше быстродействие такого устройства.

Рассмотрим свойства электромагнитного излучения.

1.1 Волновая теория излучения

Спектральный диапазон всех устройств оптоэлектроники находится в интервале мкм. Уход в более коротковолновую область привёл бы к возбуждению внутренних оболочек атомов, а более длинноволновое излучение не в состоянии вызвать ионизацию атомов.

Известно, что оптическому излучению присущ дуализм:

∙ в одной группе явлений проявляются его волновые свой-

ства;

∙ в другой — корпускулярные, квантовые.

Волновая теория излучения включает в рассмотрение явления дифракции, интерференции, поляризации, магнито-электрооптичес- ких свойств среды.

Квантовая природа оптических излучений проявляется в тепловой генерации, различных видах люминесценции, фотоэффекте, процессах взаимодействия излучения с веществом и явлениях нелинейной оптики.

12

Теоретическую основу анализа электромагнитных явлений

где E и Н — вектора напряженностей электрического и магнитно-

го полей соответственно, D — вектор электрического смещения, B

—вектор магнитной индукции, ρ — объёмная плотность заряда, ε0

—диэлектрическая проницаемость вакуума, ε — относительная

электрическая проницаемость среды, μ0 — магнитная проницаемость вакуума, μ — относительная магнитная проницаемость среды, σ — удельная проводимость среды, j — плотность тока.

Относительно материальных уравнений нужно отметить следующее. Если материал — диэлектрик, поляризующийся под действием внешнего электрического поля, то в правую часть (1.2) добавляется вектор поляризованности

где χe — диэлектрическая восприимчивость вещества, определяющаяся объёмной плотностью наведённого дипольного момента.

Если среда обладает свойствами магнетика, намагничивающегося под действием внешнего магнитного поля, то добавляется вектор внутренней магнитной индукции

(ЭМ) действуют ещё какие-либо силы электрической природы, то добавляется ещё следующее уравнение:

где EСТ — эффективная напряжённость электрического поля, характеризующая действие сторонних сил.

Совместное решение уравнений Максвелла сводится к приведению их к одному уравнению, называемому волновым, с которым связывают движение частиц. В общем случае движение час-

13

тицы описывается сложной функцией U(r,t). Волновое уравнение

где вместо U можно подставить j, E, H , A , с — скорость света. Решением (1.6) для безграничного пространства является пло-

ская монохроматическая волна, её векторный потенциал имеет вид

волновой вектор.

Анализ гармонических процессов упрощается введением метода комплексных амплитуд, знакомого из курса электротехники

и основ радиотехники. Напомним, что по формуле Эйлера e j(ωt +ϕ) = cos (ωt + ϕ) + j sin (ωt + ϕ) .

Поэтому установившиеся электромагнитные процессы, которым свойственны гармонические во времени колебания, можно записать в виде:

-находятся в бесконечности;

-в виде точечного или бесконечно протяжённого нитевидного излучателя.

Выражение (1.7) трансформируется в выражение для сферической или цилиндрической волны.

14

1.2 Распространение электромагнитных колебаний (ЭМК)

Рассмотрим бесконечно протяжённый волновод прямоугольного сечения в декартовой системе координат. Пусть оси Ох и Оy будут расположены параллельно сторонам поперечного сечения контура а и b. Любое поле в волноводе представляет суперпозицию электрического Е (Еz¹0, Hz=0) и магнитного Н (Нz¹0, Ez=0) полей.

Для каждого волновода можно записать следующие параметры:

· критические значения частоты и длины волны:

перечное волновое число, m и n — соответствуют числу полуволн, укладывающихся на стороне а и b соответственно.

Здесь lВ — соответствует длине волны в волноводе

Отсюда следует, что разные составляющие ЭМ волны имеют разные групповые скорости.

15

Например: дан прямоугольный волновод с размерами a и b , тогда

β2m = β2min = ( mπ) + ( nπ) . a b

Волна H10 — основная магнитная волна, E11 — основная электрическая (здесь силовые линии магнитного поля не могут

упираться в стенки и замыкаются сами на себе).

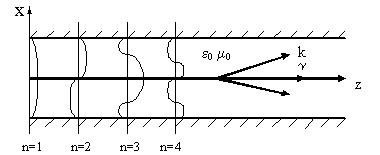
Оптическое приближение. От общего представления волн перейдем к оптическому приближению. Пусть в волноводе, состоящем из двух проводящих пластин (рис. 1.1), распространяется линейная комбинация плоских монохроматических волн с длиной волны l.

Волновой вектор волны лежит в плоскости xOz и образует

В результате отражения от верхней плоскости появляется «нисходящая» волна (– p/2 < q < 0) с комплексной амплитудой rEy. Коэффициент определяется из граничного условия Ey = 0 (при всех z) на плоскости х = а:

+ re = 0, откуда r = -e−2 jka sin θ .

В результате интерференции этих двух волн во всех точках пространства между плоскостями образуется полное поле, определяемое выражением

16

где n — положительное целое число (не путать с показателем преломления). Случай θ = 0 не удовлетворяет условиям задачи. Тогда выражение для полного поля запишется следующим образом:

Предположим, что n — четное число, то есть n = 2р. Тогда поле (нечетное) примет вид

если же n — нечетное число, то есть n = 2р+1, тогда поле (четное) будет

Соотношения (1.17) и (1.18) показывают, что вдоль оси Оz мы имеем бегущую волну с постоянной распространения в световоде

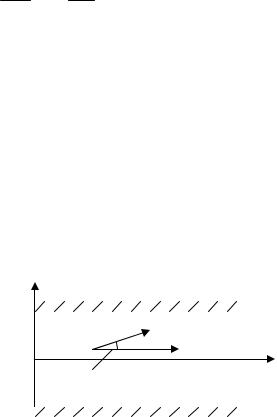
Вдоль оси х (рис. 1.2) мы имеем режим стоячих волн.

Рис. 1.2

Условие (1.16) можно рассматривать по-разному. Во-пер- вых, если рассматривать однократное прохождение волны между плоскостями туда и обратно вдоль оси х, то полный фазовый сдвиг должен быть кратным 2π. В противном случае волна будет интерферировать со всеми последующими отраженными волнами и изза гасящей интерференции быстро затухать. Под полным фазовым сдвигом следует понимать сумму фазового сдвига за счет распространения и сдвига фаз при отражениях. В металлическом световоде рассчитать полный фазовый сдвиг легко, так как отражение

17

от идеального проводника сопровождается фазовым сдвигом на π для напряженности электрического поля Еy. В результате условие согласования фаз для металлического световода запишется в виде

(−1)2 e4 jka sin θ = 1,

что и выражается соотношением (1.16).

Во-вторых, соотношение (1.16) можно рассматривать как уравнение дисперсии: оно позволяет определить постоянную распространения γ в зависимости от частоты и геометрических параметров системы. Из (1.16) и из (1.19) следует, что

Многократное отражение улучшает угловое разделение при углах θ, определяемых соотношением (1.31). Следовательно, модель двух волн вполне корректна. Нужно только учитывать, что каждая из этих волн есть сумма всех отраженных волн, четных

или нечетных.

Моды распространения. Пусть имеется генератор, способный вводить в волновод волну заданной частоты f = ω/2π. Определим, под какими углами θ волны будут распространяться в волноводе.

Положим

NωС ≤ ω ≤ (N+1) ωС (где N — целое положительное число) мы имеем N решений:

θn = arc sin(nωС/ω), n = 1,2,… N.

Каждое такое решение называется модой распространения. При всех частотах, кратных ωС, появляется дополнительная мода. На частотах, кратных 2πωС, имеем θ = π/2, то есть волна поперечная и распространения нет. Но с увеличением частоты наклон волн уменьшается.

Фазовая скорость волн находится в прямой зависимости от их угла наклона

18

Вычислим соответствующую групповую скорость:

Рассмотрим, какая мода будет распространяться при заданной частоте. Общее решение для распространяющихся мод будет линейной комбинацией этих мод с коэффициентами, зависящими в основном от условий на концах световода (излучатель и приемник). При wС £ w £ 2wС мы имеем одномодовый режим распространения. При более высоких частотах распространяется одновременно несколько мод. Каждая мода является дисперсной, и, что особенно важно, у каждой моды своя собственная дисперсия. Волновой пакет, распространяющийся в дисперсной среде, постепенно расширяется. При перемещении на расстояние l временное расширение, связанное с вкладом полосы частот w0 ± Dw, определяется выражением

Данная формула описывает влияние дисперсии моды. Как нетрудно видеть, теоретически выгодно работать как можно ближе к одномодовому режиму на сравнительно низких частотах, поскольку произведение w ×Jгр есть возрастающая функция часто-

ты.

Затухающая волна. Поскольку на частотах, меньших критической частоты, sinq получается больше 1, величина q оказывается мнимой. Если световод бесконечно длинный вдоль оси z, то

мы имеем затухающую волну.

Применение геометрической оптики. Геометрическая оп-

тика соответствует тому случаю, когда, отвлекаясь от волноводного характера поля, рассматриваются лишь направления лучей. Если волна не является плоской, но достаточно близка к ней в любой малой области (сравнимой с её длиной), основные представления геометрической оптики сохраняют смысл.

19

Как известно, при падении плоской однородной волны на границу раздела выполняются законы отражения и преломления, которые формулируются в геометрической оптике. Это не случайное совпадение: направление движения плоской волны

определяется как нормаль к её фронту — плоскости равных фаз

т.е. как прямая или луч.

Описывая произвольную волну с помощью выражения

видим, что условию постоянства фазы удовлетворяют поверхности

Лучи, характеризующие направление распространения волны, представляют собой теперь кривые линии, т.е. везде пересекающие их под прямым углом. Величина ш называется эйконалом.

Таким образом, волна (1.26) может быть принята за плоскую волну

с волновым вектором k = grad ш в достаточно малой области. Геометрическая оптика применима, если эта область в то же

время не мала в сравнении с длиной волны. Весьма существенно, что в пределе при λ → 0 законы геометрической оптики становятся справедливыми для любой волновой задачи.

20

2.ПАРАМЕТРЫ И ХАРАКТЕРИСТИКИ ЭЛЕКТРОМАГНИТНЫХ ВОЛН

Как тепловое излучение, так и люминесценция происходят при сообщении телу какой-либо энергии. ОКГ в этом отношении не представляют собой исключения, но здесь используется совершенно новый принцип превращения подводимой энергии в энергию излучения — принцип, основанный на явлении вынужденного излучения. Благодаря этому явлению, излучение лазеров обладает высокой монохроматичностью, когерентностью, направленностью и большой спектральной плотностью мощности. Кроме того, излучение большинства лазеров поляризовано. В этой главе будут рассмотрены основные оптические характеристики излучения, которые определяют широкие возможности практического исполь-

зования лазерного излучения.

Параметры электромагнитных волн. Дадим определение параметров распространяющейся волны:

Линию, совпадающую с направлением распространения волны, называют лучом.

Волновой фронт. Это — плоскость перпендикулярная лучу. В общем случае неплоской волны волновым фронтом называют такую поверхность, которая в данный момент времени характеризуется одним и тем же значением фазы ϕ .

2.1 Монохроматичность

Одной из основных характеристик излучения является ширина его спектра, т.е. диапазон частот или длин волн, который занимает излучение. Для оценки ширины спектра пользуются понятиями монохроматичности и степени монохроматичности.

Частота в оптике определяет спектральную линию излучения. Идеальных монохроматических колебаний (т.е. бесконечных во времени и имеющих постоянную амплитуду и частоту) в природе не существует.

Немонохроматичность объясняется следующими факторами: ∙ Время существования любых волн — конечно.