Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Томский Государственный Университет Систем Управления и Радиоэлектроники

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Расчет диэлектрических волноводов и объемных резонаторов

..pdf

Скачиваний:

Добавлен:

05.02.2023

Размер:

1.98 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 127 8 9 10 11 12 > Следующая >>>

E z р

A sin(

1 у )cos

cos 1 у sin

z , область I,

(3.13)

E xр

A cos 1

H yр

e - 2 y cos

e 2

y sin

область II .

(3.1.4)

cos

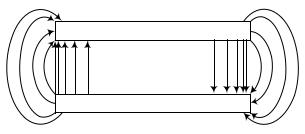
В этих уравнениях l определяет количество полуволн, укладывающихся вдоль резонатора, h –продольный размер резонатора. Структура поля колебания

Е021 показана на рис.16.

Рис.16 Структура поля колебания Е021

3.2 Планарные диэлектрические резонаторы.

Под планарным резонатором подразумевается резонатор, образованный двумя параллельными металлическими пластинами, расположенными на расстоянии h значительно меньшем длины волны в диэлектрике d ( h << d ).

По существу это может быть, плѐнка на которую с двух сторон напылѐн металл.

Так как h << d , в этом направлении поле может быть только однородным. Если

c ним совместить ось Z, то в уравнениях Максвелла необходимо положить

		0	. По этой же причине в резонаторе будет отсутствовать	продольная

	z
	z
магнитная составляющая поля Н z .
			Конфигурация резонатора может быть разнообразной. Резонаторы		могут
быть			прямоугольными, круглыми, эллиптическими, кольцевыми.	В	данном
пособии рассмотрены первые два типа - прямоугольный и круглый.

3.2.1Круглый планарный диэлектрический резонатор.

1.Вывод уравнений, определяющих структуру поля в резонаторе.

Расчет параметров резонатора.

Уравнения Максвелла, описывающие электромагнитное поле в резонаторе

имеют вид:

r o t E

j 0 0 H

0 H

k 0 H z ,

r o t H j 0 0 E

0 E

k 0 E z ,

															63

			0		0	k 0						0		0	k 0

	1						0	=-j 0 Н ,		1						0	= j a E . (3.2.1)
r o t E	1								r o t H	1
r o t E									r o t H

		E		E		E z					H		H		H z

Откуда


		1		1	E z
Н	j
Н	j
			0
		1		1	E z
Н		j
Н		j
		0

(3.2.2)

(3.2.3)

Так как в резонаторе могут существовать только продольные электрические поля, для решения уравнений Максвелла достаточно найти составляющую Е z ,

решив волновое уравнение:

	2 E z	1	2 E z	1	2 Е z	2 E			.	(3.2.4)
						2 E		z	.	(3.2.4)
	2	2		2	2			z
	2	2		2	2
Решением этого уравнения является выражение
E z ( A J m ( ) N m ( )) cos							m		,

в котором для удовлетворения требований теоремы единственности нужно положить N m =0.

Так как в данном резонаторе при а проходит граница диэлектрик-

диэлектрик, для определения неизвестных констант необходимо применить

граничные условия Олинера:	Е z	0 . В результате получим выражение для Еz:
граничные условия Олинера:		0 . В результате получим выражение для Еz:

	Еz= Ez0		Jm(	mn	)cos(mα),	(3.2.5)
	Еz= Ez0		Jm(	a	)cos(mα),	(3.2.5)
				a

где

- корень производной функции Бесселя.

Подставляя (3.2.5) в (3.2.2), (3.2.3), получим выражения для составляющих

векторов поля колебаний типа Emn0:

(

) cos( m ) ,

z 0

J m

(

) sin( m ) ,

(3.2.6)

jH 0

J m

(

) cos( m )

где

H 0

E z 0

H 0 E z 0

2. Расчѐт геометрических размеров резонатора

Основным отличием рассматриваемого резонатора от обычного замкнутого

резонатора является отсутствие боковых металлических поверхностей.

Диэлектрик, находящийся между металлическими пластинами, с относительной диэлектрической проницаемостью r при а граничит с воздухом. В

результате чего электромагнитное поле выходит за пределы резонатора и частично находится в воздухе (рис.17).

εr

Рис. 17 Геометрия круглого планарного резонатора

Поэтому целесообразно резонатор с неоднородным заполнением заменить эквивалентным ему резонатором с однородным диэлектриком, относительная диэлектрическая проницаемость которого равна εr эф (рис.18) .

εr эф

Рис. 18 Геометрия эквивалентного резонатора

Эквивалентный резонатор будет обладать «эффективными» размерами,

отличными от тех, которые были бы у резонатора закрытого металлическими боковыми поверхностями. Резонансная длина волны при этом будет определяться

формулой

2 a эф

r эф

(3.2.7)

2 h

где

а эф a 1

1,773

(3.2.8)

2 h

Для определения εr эф пользуются соотношением [1]:

r эф

C эф

(3.2.9)

C эф1

где

C =

+ C

C 1

= C

+ C 1

(3.2.10)

эф

0 эф

kэф

эф

0 эф

kэф

C 0 эф

a 2

J '

(

) J '

(

)

(3.2.11)

m 1

0 h

J 'm2 ( mn )

C kэф

a 120

( 2 а , h ,1)

(3.2.12)

Z W ( а , h , r )

					66
0	1,		при	m 0	.
		2 ,	при	m 0

Z W ( 2 a , h ,1) - волновое сопротивление НПЛ с шириной полоски 2a с воздушным

заполнением,

Z W ( 2 a , h , r ) - волновое сопротивление НПЛ с шириной полоски

2a с диэлектрическим заполнением:

120

2 а

( 2 a , h ,

)

(ln( 17

( а / h

0 ,92 ))

(3.2.13)

При расчѐте

Z W ( 2 a , h ,1)

в формулу (3.2.13)

вместо r

нужно подставлять 1:

2 а

Z W ( 2 a , h ,1)

120

(ln( 17 ( а / h 0 ,92

)) .

3. Расчѐт добротности резонатора

В резонаторе существует два вида потерь: потери в диэлектрике и потери в металле. В результате чего полная добротность резонатора определяется по известной формуле:

					1		1	1		.	(3.2.14)
										.	(3.2.14)
						Q п	Q м	Q d
Здесь	1		tg	, где	tg - тангенс угла потерь диэлектрика,						который обычно

		Q d
		Q d
известен.
	Полагая, что пластины резонатора выполнены из высокопроводящего
металла с проводимостью м , находим
							Q м	h	,		(3.2.15)
							Q м		,		(3.2.15)

							67

где 1 /		0 м	- глубина проникновения поля в металл.
где 1 /	2		- глубина проникновения поля в металл.
	2
Полная добротность резонатора равна:
			Q п	Q d Q м		.	(3.2.16)
			Q п	Q d	Q м	.	(3.2.16)
				Q d	Q м

3.2.2 Прямоугольный планарный резонатор

В качестве исходных данных задаются: тип колебаний Emnp (например: E110,

т.е. m=1, n=1, p=0), рабочая частота f0, толщина диэлектрика h, относительная диэлектрическая проницаемость εr , окружающая среда - воздух.

1 . Уравнения, определяющие структуру поля

Для вывода уравнений, определяющих структуру поля, можно

воспользоваться инвариантной формой

grad

j grad

(3.2.17а)

grad

j grad

(3.2.17б)

где

e1 H q

2 H q

;

e1 E q

2 E q

;

grad

q 2

Так как в резонаторе отсутствует продольная составляющая магнитного

поля

Н z и поле не

распространяющееся

( 0 ),

находим

составляющие

поперечного магнитного поля из уравнения (3.2.17б):

grad

0 ,

(3.2.18)

j a

Е z

где H

i H

;

; grad

Они выражены через

составляющую Еz, которую определим из волнового

уравнения

2 E z

2 E

х 2

у 2

и его общего решения

Еz=(Acoskxx+Bsinkxx)(Ccoskyy+Dsinkyy).

Применив граничные условия Олинера:

Е z

0 при х=0, х=а

Е z

при у=0, у=b, получим выражение для Еz :

Еz=Еz0coskxx coskyy,

(3.2.19)

где

2 k 2

k 2 , k

(3.2.20)

2. Структура поля

Используя (3.2.18), найдем выражения, определяющие структуру поля:

E z

E z 0 cos

x cos

y ,

H x

jH x 0

cos

x sin

y ,

H y jH y 0 sin

x cos

y ,

a b

a a

где Нx0=Еz0

, Нy0=Еz0

3. Резонансная длина волны

Для волны типа Еmn она определяется выражением

рез

r эф

(3.2.21)

эф

где m - количество вариаций поля по оси X,

n -количество вариаций поля по оси

Z, r эф

-эффективная

относительная

диэлектрическая

проницаемость

диэлектрика

однородно.

а эф , b эф - эффективные размеры пластины. Вдоль оси Y поле

4. Эффективная диэлектрическая проницаемость

Эффективная диэлектрическая проницаемость находится как

r эф

С эф

(3.2.22)

С эф1

где C

-эффективная ѐмкость

резонатора прямоугольного

сечения

эф

диэлектрической относительной

проницаемостью диэлектрика

;

эф

эффективная ѐмкость резонатора прямоугольного сечения с диэлектрической относительной проницаемостью диэлектрика r =1.

В общем случае эффективная ѐмкость C эф определяется выражением

= C

+2 C

(3.2.23)

эф

0 эф

k 1 эф

k 2 эф

где

-эффективная ѐмкость плоского конденсатора,

0 эф

Z W ( а , h ,1)

120

C k 1 эф

2 ( а , h ,

)

Z W ( b , h ,1)

120

C k 2 эф

2 ( b , h ,

)

, C

- эффективные краевые ѐмкости.

k 1 эф

k 2 эф

(3.2.24)

(3.2.25)

Ёмкость C 1	вычисляется по этим же формулам, но вместо	r	в них надо
эф		r
подставить 1.
В вышеприведенных формулах 1 при n =0 , 2 при n 0			; 1 при
m =0, 2 при	m 0 ; Z W ( а , h , r ) - волновое сопротивлении несимметричной

полосковой линии, у которой a -ширина полоски; h, r -толщина и относительная

диэлектрическая проницаемость подложки.

При вычислении C		Z	W	( b , h ,	r	) -	волновое сопротивлении
	k 2 эф		W		r
несимметричной полосковой линии,		у которой b -					ширина полоски,	h, r -

толщина и относительная диэлектрическая проницаемость подложки :

Z W

( а , h , r

) =

120

(ln( 17 ( а / 2 h

0 ,92 ))

Z W

( b , h , r

) =

120

(ln( 17 ( b / 2 h

0 ,92 ))

, (3.2.26)

. (3.2.27)

Значения а эф и b эф , входящих в формулу (3.2.21),

определяющую рез равны:

120 а

а эф

(3.2.28)

( а , h ,

)

эф

<<< < Предыдущая 1 2 3 4 5 67 / 127 8 9 10 11 12 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
05.02.20239.2 Mб16Распределенные сервис-ориентированные системы..pdf
#
05.02.2023283.13 Кб10Распространение лазерных пучков..pdf
#
05.02.20235.51 Mб95Распространение радиоволн и антенно-фидерные устройства..pdf
#
05.02.20231.52 Mб46Распространение радиоволн..pdf
#
05.02.2023425.46 Кб15Расчет деформационно-прочностных свойств композиционных материалов и напряженно-деформированного состояния простейших конструкций..pdf
#
05.02.20231.98 Mб32Расчет диэлектрических волноводов и объемных резонаторов..pdf
#
05.02.2023259.91 Кб14Расчет допусков и посадок сопрягаемых деталей..pdf
#
05.02.2023306.65 Кб20Расчет импульсной и переходной характеристик цепи..pdf
#
05.02.2023332.92 Кб34Расчёт надёжности функционального узла РЭС..pdf
#
05.02.20232.43 Mб12Расчет неуправляемого выпрямителя..pdf
#
05.02.2023131.15 Кб14Расчет переходных процессов классическим и операторным методами в цепях второго порядка..pdf