
Расчет диэлектрических волноводов и объемных резонаторов
..pdf
|
|
|
|
|
|
|
|
|
|
|
51 |
функций |
Бесселя |
|
для поверхностных |
волн |
становится |
мнимым, |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
j |
2 2 |
0 |
|
0 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Поэтому общее |
|
решение волнового |
уравнения |
в этой области |
является |
||||
суммой двух частных решений, которое при мнимых аргументах является суммой цилиндрических функций третьего рода I 0 ( 2 ) и четвѐртого рода K0( 2 ):
H IIz =C I 0 ( 2 ) D K0( 2 ). Они называются функциями Макдональда и носят не
колебательный, а монотонно изменяющийся |
характер: I 0 ( 2 ) стремится к |
бесконечности при , а функцией K0( 2 |
) стремится к нулю при . |
В соответствии с требованием теоремы единственности нужно исключить
I 0 ( 2 ) , положив С=0, и удержав функцию K0( 2 ) записать Н zII = DK0( 2 ).
В результате решение волнового уравнения для круглого волновода окончательно запишется:
|
|
Н zI |
=AJ0( 1 ), |
область I |
0 а , |
( 2.4.4) |
|
|
Н zII |
= DK0( 2 ), |
область II |
а , |
( 2.4.5) |
здесь А= Н |
I |
, D= Н |
II - амплитуды продольных составляющих магнитного поля |
|||
|
z 0 |
|
z 0 |
|
|
|
для первой и второй областей соответственно. |
|
|
||||
Воспользовавшись формулами (2.4.1), |
для волн типа Н0n |
найдѐм: |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
52 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
E I |
|
j |
|
|
|
|
|
|
|
|
|
H zI 0 |
J 1 ( 1 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
H I |
j |
|
|
|
|
|
|
|
|
H zI |
0 |
J 1 ( 1 ) , |
|
|
|
|
|
для области I, |
|
|
|
( 2.4.6) |
|||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
H |
I |
H |
|
I |
|
|
|
J |
0 |
( |
1 |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
z |
|
|
|
|
z 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
E II |
|
j |
|
|
|
|
|
|
|
|
|
H zII0 |
K 1 ( 2 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H II |
j |
|
|
|
|
|
|
|
H zII0 K 1 ( 2 |
) , |
|
|
|
для области II. |
|
|
|
( 2.4.7) |
|||||||||||||||||||||
|
2 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Н |
II |
H |
II |
|
K |
0 |
( |
2 |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
z |
|
|
|
|
|
z 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
|
|
|
|
|
|
|
|
|
II |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
II |
I J 0 ( 1 а ) |
|
||||||
Из граничного условия |
Н z |
= Н z |
|
при |
а , найдѐм |
|
Н z 0 |
= H z 0 |
|
|
|
|
. |
||||||||||||||||||||||||||
|
|
K 0 ( |
2 |
а ) |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Для вывода дисперсионного уравнения приравняем тангенциальные |
|||||||||||||||||||||||||||||||||||||||
составляющие E II = E I |
|
|
|
и |
|
|
|
|
|
|
|
Н zI |
= Н zII |
на границе диэлектриков при |
а , |
||||||||||||||||||||||||
|
|
|
0 |
|
|
H |
|
|
I |
J |
|
( |
|
а ) |
0 |
Н |
II K |
|
( |
|
а ) |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
z 0 |
1 |
1 |
|
1 |
2 |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
z 0 |
|
. |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
H |
I |
|
|
J |
0 |
( |
1 |
а ) H |
II |
K |
0 |
( |
2 |
а ) |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
z 0 |
|
|
|
|
|
|
|
|
|
|
|
|
z 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Поделив второе уравнение на первое, получим дисперсионное уравнение
|
1 a |
J |
0 |
( 1 a ) |
|
2 a |
K 0 |
( 2 a ) |
. |
( 2.4.8) |
|
J 1 ( 1 a ) |
K 1 ( 2 a ) |
||||||||||
|
|
|
|
|
|
||||||
Это трансцендентное дисперсионное уравнение можно решать на ЭВМ или графически. Графическое решение является менее точным, но более наглядным.
Поэтому оно будет рассмотрено в примере ниже
5. Так как фазовая скорость едина для первой и второй областей, то и
53
волновое число одинаково для быстрых и медленных волн и равно
|
|
2 |
0 |
|
0 |
2 |
и |
|
|
|
|
|
|
|
2 |
0 |
|
а |
|
|
2 . Следовательно справедливо равенство |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
2 |
0 |
|
0 |
|
2 = |
|
2 |
0 |
|
а |
2 |
, |
из которого |
вытекает уравнение, |
связывающее |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
неизвестные |
|
1 |
и |
2 |
: |
|
|
( |
1 |
а ) |
2 |
( |
2 |
а ) |
2 ( а ) |
2 ( |
0 |
|
а |
|
0 |
|
0 |
) = R 2 . |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
Как и в случае прямоугольных диэлектрических волноводов, получилось |
|||||||||||||||||||||||||||||||||||||||||||
уравнение окружности радиуса R |
|
|
|
|
|
|
|
|
2 a |
|
|
|
в координатах |
|||||||||||||||||||||||||||||||||
|
0 0 a |
|
r |
|
1 |
|
|
r 1 |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 а |
и 2 а . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Совмещение окружности и графического изображения дисперсионного уравнения позволяет найти радиус волновода для заданного типа волны, что и является конечной целью задачи.
Заметим, что |
|
2 |
|
2 |
0 |
|
0 |
2 |
|
j |
2 |
2 |
0 |
|
0 |
|
отрицательна и |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
поэтому решение будет находиться в отрицательной части |
|
|
дисперсионного |
|||||||||||||||||||||
уравнения. При большом 2 |
волна будет иметь ярко выраженный поверхностный |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
характер, при этом |
|
2 |
, но одновременно |
|
1 |
, |
|
1 |
= |
|
|
2 |
0 |
|
а |
2 . |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Проанализируем дисперсионное уравнение с точки зрения определения поперечных чисел. Правая часть дисперсионного уравнения (2.4.8) является
функцией |
2 а , а левая |
1 а . Отношение |
|
K 0 |
( 2 a ) |
можно положить равным 1. |
||||
|
K 1 |
( 2 a ) |
||||||||
|
|
|
|
|
|
|
|
|
||
Тогда |
1 a |
J 0 |
( 1 a ) |
|
|
а . Левая часть |
дисперсионного уравнения - функция |
|||
J 1 |
( 1 a ) |
2 |
||||||||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
54 |
|||
F 1 |
( x ) x |
J 0 |
( x ) |
, |
где x |
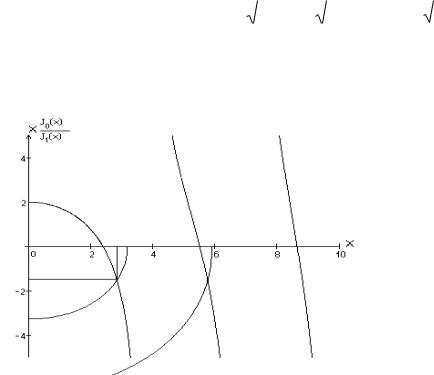
1 a . Построим график зависимости этой функции (рис.14) |
|||||||||||||||
J 1 |
( x ) |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
от |
аргумента |
x 1 а , |
который откладываем |
по оси |
абсцисс. Правая часть |
||||||||||||||||
дисперсионного |
уравнения |
- |
функция |
F 2 ( у ) y , |
где |
y 2 a . |
Построим |
||||||||||||||
|
x 2 |
|
y 2 R 2 , где |
|
|
|
|
|
|
|
|
2 a |
|
|
|
||||||
уравнение окружности |
|
R |
|
0 0 |
a |
|
r |
1 |
|
|
r 1 на |
||||||||||
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
рис.14. Найдем точки пересечение окружности с кривой |
F 1( x ) . |
|
|
|
|||||||||||||||||
Рис. 14 Графическое решение дисперсионного уравнения Они определяют рабочие точки и количество типов колебаний, которые могут
распространяться по волноводу. Из рис.14 видно, что при R<2,405, на самой низкой частоте пересечений нет, а следовательно нет корней дисперсионного уравнения. С увеличением радиуса окружности сначала появляется один корень,
затем два и так далее. Как видно, все они |
|
лежат между нулями и полюсами |
|||||||||||||
функции |
|
|
а |
J 0 |
( 1 а ) |
, то есть между нулями |
J |
0 ( 1 а ) |
(функция |
|
|
а |
J 0 |
( 1 а ) |
равна |
1 |
J 1 ( 1 а ) |
1 |
J 1 ( 1 а ) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
55 |
нулю) и нулями J 1 ( 1 а ) (функция |
1 а |
J |
0 ( 1 |
а ) |
обращается в бесконечность), а это |
|||||||||||||||||||||
|
J 1 ( 1 а ) |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
корни 0 m и 1 m функций J 0 |
( 1 а ) |
и J 1 ( 1 а ) , соответственно. |
|
|||||||||||||||||||||||
При критической частоте f=fкр, |
для |
которой |
|
|
2 |
0 , поле утрачивает |
||||||||||||||||||||
продольную составляющую (Еz=0, Нz=0) и становится Т-волной. |
В случае f<fкр |
|||||||||||||||||||||||||
волна распространяется во второй среде, то есть во внешнем пространстве. |
||||||||||||||||||||||||||
При этом постоянная |
распространения |
|
|
|
|
|
|
|
|
= 2 . |
При 2 0 |
|||||||||||||||
|
|
|
|
2 2 |
||||||||||||||||||||||
J 0 ( 1 а ) 0 , 1 а 0 n и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 n |
|
|
|
с |
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
|
|
|
кр |
|
|
|
|
|
|
|
или |
кр |
|
|
|
2 |
|
r 1 |
1 . |
(2.4.9) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
а |
|
|
|
r 1 |
1 |
|
|
|
|
0 n |
|
|
|
|
|
|
|
|
||||||
Так как условия распространения волн в волноводе выполняются тогда, |
||||||||||||||||||||||||||
когда кр или кр , то, как обычно, можно |
|
|
взять равной 0,8 кр и из |
|||||||||||||||||||||||
формулы (2.4.9) определить радиус волновода для заданного типа колебания
а |
|
0 n |
|
|
с |
|
|
0 n |
|
|
|
|
. |
(2.4.10) |
0 ,8 |
|
|
|
|
1,6 |
|
|
|
|
|||||
|
|
r 1 1 |
|
|
|
r 1 1 |
||||||||
|
|
|
|
|
|
|
|
|
|
|||||
Мощность, канализируемая по круглому волноводу.
Волны типа H 0 n .
Как и в случае прямоугольного диэлектрического волновода, мощность
канализируется по двум областям: в области I ( 0 а ) - Р срI и в области II
( а ) - Р срII .
Для определения средней мощности используем формулу Р ср П ср dS ,
S
56
ds= . Запишем выражения для средней мощности:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
II |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Р срIH |
|
|
|
1 |
|
|
|
|
|
Z W |
|
|
|
|
|
Н zI |
2 |
|
|
|
|
|
Р срIIH |
|
1 |
|
|
|
|
Z W |
|
|
|
|
Н zII |
|
2 |
|
|
|||||||||||||||||||||||
через H z для волн типа Н - |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ds , |
|
|
|
|
|
|
|
|
|
|
|
|
|
ds |
, |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
22 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s |
|
|
|
|
|
|
|
|
|||||||||||||
где Z |
I |
Z |
II |
|
0 |
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
W |
W |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
и через Е z |
для волн типа Е – Р |
срIE |
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
E zI |
|
|
2 |
ds |
, |
Р срIIE |
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
E zII |
|
2 |
ds |
, |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
2 |
|
|
|
|
2 |
Z |
|
|
I |
|
|
|
|
2 |
|
|
|
|
2 |
Z |
II |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
W |
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
W |
|
|
s |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
где Z |
I |
|
|
|
|
|
|
, |
Z II |
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
W |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
a |
|
|
W |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
2 |
|
|
|
|
|
1 |
|
|
|
|
|
m |
2 |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
Используя |
|
|
выражение |
|
|
|
|
J m2 |
( ) d |
|
|
|
|
J m2 ( ) |
( а 2 |
|
|
|
) J m2 |
( ) , |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||||||||||
получим для поля не зависящего от : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
2 |
I |
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
I |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Р срIH |
|
|
1 |
|
|
|
Z W |
( Н zI 0 ) 2 |
|
J 02 ( 1 ) d |
1 |
|
|
|
Z W |
a |
|
( Н zI 0 ) 2 ( J 02 |
|
|
( 1 а ) J 02 ( 1 а )) = |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
2 |
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
1 2 Z WI a |
2 |
|
|
|
|
|
I |
|
|
2 |
|
|
|
|
|
2 |
|
1 а ) |
|
|
|
2 |
( 1 а )) , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.4.11) |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( Н z 0 ) |
|
(J |
|
|
0 ( |
|
J |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
II |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Р срIIН |
|
|
1 |
|
|
|
Z W |
( Н zII0 ) 2 K 02 ( 2 ) d = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
= |
1 |
|
2 Z WII |
|
a 2 |
|
( Н zII0 ) 2 |
( K 02 |
|
( 2 а ) K 02 |
( 2 а )) |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.4.12) |
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
Pср = PсрI + PсрII |
= |
|
|
|
0 |
a 2 |
|
|
|
1 |
|
|
( Н zI 0 ) 2 ( J 02 ( 1 а ) J 02 ( 1 а )) + |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
57 |
|
+ |
1 |
( Н zII0 ) 2 ( K 02 ( |
2 а ) K 02 |
( 2 а )) , |
(2.4.13) |
|||||
22 |
||||||||||
|
|
|
|
|
|
|
|
|
||
где в (2.4.13) использовано соотношение Z |
I |
Z |
II |
|
0 |
. |
|
|||
W |
W |
|
|
|||||||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||
Волны типа Е 0 n .
1. Структура волн типа Е0n. Уравнения, определяющие структуру поля
|
Н I |
j |
|
а |
|
Е zI 0 J 1 ( 1 ) |
|
|
Н II |
j |
|
0 |
|
Е zII0 |
K 1 ( 2 ) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Е I |
|
j |
|
|
|
Е zI |
0 J 1 ( 1 ) |
для обл.I, |
|
Е II |
j |
|
|
|
|
|
Е zII0 |
K 1 ( 2 ) для обл.II . (2.4.14) |
|||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
1 |
|
2 |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Е I |
Е |
I |
J |
0 |
|
( |
1 |
) |
|
Е II |
Е |
II |
K |
0 |
( |
2 |
) |
|||||||||
|
z |
|
z 0 |
|
|
|
|
|
|
|
z |
|
z 0 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. Дисперсионное уравнение.
|
r 1 |
|
|
a |
J 0 |
( 1 a ) |
|
|
a |
K 0 |
( 2 a ) |
. |
(2.4.15) |
|
|
1 |
|
|
2 |
|
|
||||||
|
r 2 |
|
|
J 1 |
( 1 a ) |
|
|
K 1 |
( 2 a ) |
|
|||
|
|
|
|
|
|
|
|
||||||
3. Определение поперечных |
1 |
и |
|
2 |
и продольной |
постоянных |
|||||||
распространения производится аналогично рассмотренному ранее для магнитных волн.
4. Мощность канализируемая по волноводу
Р срIE |
1 |
|
|
2 |
|
|
E zI |
|
2 |
ds , |
Р срIIE |
1 |
|
|
2 |
|
|
E zII |
|
2 |
ds . |
||
|
|
|
|
|
|
||||||||||||||||||
|
|
|
2 |
I |
|
|
|
2 |
2 |
II |
|||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
1 |
Z W |
S |
|
|
|
|
|
|
2 |
Z W |
s |
|
|
|
|
|
||||||
Откуда:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
58 |
|
|
1 |
|
|
2 |
2 |
|
|
|
|
|
|
a |
|
|
|
|
|
|
1 |
|
|
|
2 |
a |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Р срIE |
|
|
|
|
|
( E zI |
0 ) 2 |
J 02 ( 1 ) d |
|
|
|
|
|
|
|
( E zI |
0 ) 2 |
( J 02 |
( 1 а ) J |
02 ( 1 а )) , |
|
(2.4.16) |
||||||||||||||||||||||||||
2 |
|
2 Z |
I |
|
|
|
|
2 |
Z |
|
|
I |
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
1 |
W |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
W |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
IIE |
|
|
1 2 2 |
|
II |
|
2 |
a |
|
2 |
|
( 2 ) d |
= |
|
1 2 a |
|
2 |
|
II |
|
2 |
|
|
2 |
|
1 а ) |
|
2 |
( 1 а )) |
, |
(2.4.17) |
|||||||||||||||||
Р ср |
|
|
|
|
|
|
|
|
|
( E z 0 |
) |
|
|
K |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
( Е Z 0 |
) |
|
( K |
0 |
|
( |
K |
0 |
|||||||||||
2 |
|
2 Z |
II |
|
|
2 |
|
|
2 Z |
|
II |
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
2 |
W |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
W |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
где Z |
I |
= |
|
|
|
|
|
|
и |
|
Z |
|
II |
= |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
W |
|
а 1 |
|
|
W |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
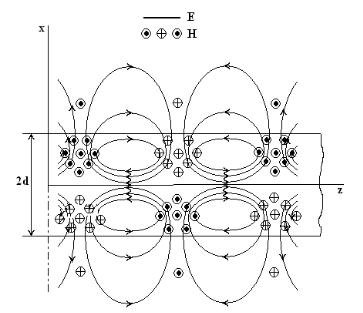
В качестве примера на рис.15 представлена структура полей волны E01.
Рис. 15 Структура полей волны E01
59
ГЛАВА 3 РАСЧЕТ ОБЪЁМНЫХ РЕЗОНАТОРОВ
3.1 Диэлектрический Н-образный резонатор
На базе рассмотренных выше волноводов можно создать резонатор,
который называют Н - образным диэлектрическим резонатором. Для этого необходимо волновод ограничить металлическими торцевыми стенками. Если расстояние между торцевыми стенками взять кратным половине длины волны в волноводе, то в резонаторе возникнет резонанс. При расчѐте резонатора необходимо после расчѐта волновода произвести:
1. Определение продольного размера объѐмного резонатора. Он равен количеству полуволн l, укладывающихся при резонансе вдоль резонатора:
h=l |
в |
. |
|
|
|
(3.1.1) |
|
|
|
|
|||
2 |
|
|
|
|
|
|
2. Определение собственной добротности резонатора. |
|
|
|
|
||
Добротность резонатора определяется из формулы: |
Q |
W |
. |
Здесь - |
||
|
||||||
|
|
|
|
P |
|
|
угловая резонансная частота резонатора, W - энергия, запасѐнная в резонаторе,
Р - мощность потерь в резонаторе в единицу времени. В рассматриваемом резонаторе потери возникают в диэлектрике за счѐт протекающих в нем токов проводимости - d d Е , а также в торцевых металлических пластинах, за счѐт протекающих по ним токов проводимости - м Н .
Собственная добротность резонатора Q0 при учѐте потерь в диэлектрике и в торцевых стенках может быть определена из известной формулы:
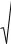
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
60 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
1 |
. |
|
|
|
|
|
(3.1.2) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
Q 0 |
|
|
Q 0 d |
|
Q 0 м |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Добротность |
Q 0 d |
|
|
a E 2 dv |
|
|
|
1 |
|
|
|
может |
быть определена при |
||||||||||||||||||
d E 2 dv |
|
|
|
|
tg |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
известном tg |
диэлектрика. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Добротность, обусловленная потерями в торцевых стенках, может быть |
|||||||||||||||||||||||||||||||
определена из интеграла: |
|
Q 0 м |
|
|
0 |
|
v H 2 dv |
|
|
в |
. |
|
|
|
|||||||||||||||||
|
|
2 м |
H 2 ds |
|
16 |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Здесь в |
-длина волны в |
волноводе, |
|
|
|
-глубина |
проникновения поля в металл, |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
которая |
равна |
|
1 / |
0 м |
. |
Так |
|
|
как |
проводимость |
металла |
очень высока |
|||||||||||||||||||
|
|
2 |
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(например, для |
меди |
|
|
она |
|
равна |
|
|
5 ,8 10 7 См/м), |
|
то |
потери |
в |
резонаторе |
|||||||||||||||||
практически определяются только потерями в диэлектрике. Так при |
tg 10 3 , |
||||||||||||||||||||||||||||||
добротность резонатора |
|
|
Q 0 1000 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
3. |
Структура поля |
строится |
на |
|
|
основании уравнений, |
определяющих |
||||||||||||||||||||||||
структуру поля в резонаторе. Для получения этих уравнений необходимо уравнения, определяющие структуру поля в соответствующем волноводе,
подчинить граничным условиям на торцевых стенках резонатора, т.е. потребовать выполнения граничных условий на границе диэлектрик-металл: Е 0 , Н max .
Например, в случае волн электрического типа уравнения, определяющие структуру поля, будут иметь вид
