Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Томский Государственный Университет Систем Управления и Радиоэлектроники

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Расчет диэлектрических волноводов и объемных резонаторов

..pdf

Скачиваний:

Добавлен:

05.02.2023

Размер:

1.98 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 125 6 7 8 9 10 11 12 > Следующая >>>

Определение констант.

Для определения констант и вывода дисперсионных уравнений используем

граничные условия на границе диэлектрик-диэлектрик:

H 1 =H 2 , E 1	= E 2	при у=0, или	Hz1=Hz2		, Eх1= Eх2 ,
H 2 =H 3 , E 2	= E 3	при у=-d, или	Hz2=Hz3	,	Eх2= Eх3 .

Для волн типа Н0n составим систему 4-х уравнений:

1.Hz1=Hz2

2.Eх1= Eх2

3.Hz2=Hz3

4.Eх2= Eх3

при y=0 ,	откуда A1= A2 =C ,													(2.3.6)
при y=0, откуда			2	C=- B			,							(2.3.7)
при y=0, откуда				C=- B		2	,							(2.3.7)
			1			2
			1
при y=-d ,	откуда		A3 = С (cos				2 d	2		sin		2 d ) ,		(2.3.8)
при y=-d ,	откуда		A3 = С (cos				2 d			sin		2 d ) ,		(2.3.8)
								1
при y=-d,	откуда	А3= C (			3	sin	2 d		3		cos		2 d ) .	(2.3.9)
при y=-d,	откуда	А3= C (			2	sin	2 d		1		cos		2 d ) .	(2.3.9)
					2				1

Окончательные уравнения, определяющие структуру поля волн типа Н0n,

запишутся в виде:

Ну1=j			Cе 1 у ,
Ну1=j	1		Cе 1 у ,
	1
Eх1=j		0		Cе	у	,	область I	0 у ,	( 2.3.10а)
Eх1=j				Cе	1	,	область I	0 у ,	( 2.3.10а)
	1
Hz1 = Cе		1 у			.
Hz1 = Cе					.

Hу2= j

(sin 2 y

2 y )

cos

Ех2=

jС 0

( sin

cos 2

y ) , область II -d

y 0

, (2.3.10б)

Hz2= С (cos

sin 2 y ) .

Ну3=-jA3

3 ( d

у )

Eх 3=-j

A3е 3

( d ) у ,

область III - y d

(2.3.10в)

Hz3=A3е 3 ( d у ) ,

где А3 в Hz3 и Eх3 дается соответственно выражениями (2.3.8) и (2.3.9).

Для вывода дисперсионного уравнения приравняем (2.3.8) и (2.3.9):

				cos				d		2		sin		d		=	3	sin		d	3	соs		d ,	(2.3.11)
				cos			2	d				sin	2	d		=		sin	2	d		соs	2	d ,	(2.3.11)
							2				1		2						2		1		2
											1						2				1
или (	3	2	) sin			d = (			3		1) cos					d .
	3	2			2										2
	2	1							1


	Разделим левую и правую части этого уравнения на cos 2 d																								и проведя

простые преобразования получим окончательное выражение дисперсионного уравнения для волн типа Н0n

tg ( 2 d )	1		( 1	3 )			.	(2.3.12)
tg ( 2 d )		2	(1	1	3	)	.	(2.3.12)
				1	3
				2
				2
				2

Уравнения, определяющие структуру поля волн Н0n , можно также записать

и в следующем виде:

								1	y					j z																									y )
		Ce						1		e							,																	при		( 0			y )
																				2					2 у )) e				j z ,												(2.3.13а)
H z	( у , z )	C (cos(								2 у )										2		sin(												при		( d			y 0 )
H z	( у , z )	C (cos(								2 у )									1			sin(												при		( d			y 0 )
																			1
																		2							2 d )) e				3 ( d y ) e j z , при
		C (cos(								2 d )								2				sin(														(			y d )
		C (cos(								2 d )									1			sin(														(			y d )
																			1
			0							1 y e j z																											y )
		j				Ce												,															при		( 0
		j	1			Ce												,															при		( 0
			1

			0																2							у ) e j z ,														,	(2.3.13б)
E x	( у , z ) j		0			C (sin								2 у					2			cos		2										при	( d			y 0 )
E x	( у , z ) j		2			C (sin								2 у					1			cos		2										при	( d			y 0 )
			2																1
						0						3												3		cos( 2 d )) e 3					( d y ) e j z , при
			j			0			C (			3			sin(			2 d )						3												(			y d )
			j	3					C (			2			sin(			2 d )						1												(			y d )
				3								2												1
					Ce 1 y e j z ,																												( 0		y )
		j																														при
		j	1																													при
			1

					1																2								j z											,	(2.3.13в)
H y ( у , z )		j C							(sin(					2 у )									cos(				2 у )) e			,		при		( d		y 0 )
H y ( у , z )		j C			2				(sin(					2 у )							1		cos(				2 у )) e			,		при		( d		y 0 )
					2																1
								1					3												3							( d y )		j z
			j C					1					3						2 d )						3			cos( 2 d )) e				( d y )		j z						y d )
											(					sin(																3	e		, при		(
							3				(		2			sin(									1							3	e		, при		(
							3						2												1

причем Ez=Ey=Hx =0.

Преобразование дисперсионного уравнения.

Преобразуем дисперсионное уравнение (2.3.12)

			1			1	3
								, записав						,			2 n	2	2 ,		2	k	2 n	2	,
tg(		d )								2	k	2 n	2			k		2						2
tg(	2	d )							1	2	k	2 n	1		2	k		2		3				3
	2						1 3		1			0	1		2		0	2		3			0	3
				2	1		1 3
				2	1		2
							2
							2

																														1												2 k					2 n 2								2 k								2 n		2
												2 n			2			2 d )												1												2 k					2 n 2								2 k								2 n		2
						tg (				k					2																																0 1																0	3								.
						tg (				k					2																																																									.
												0			2													2 n		2				2										2 k 2 n 2																2 k 2 n							2
																										k		2 n		2				2										2 k 2 n 2																2 k 2 n							2
																												0	1								(1										0			1													0				3				)
																																					(1											k 2 n			2 2																				)
																																																k 2 n			2 2
																																															0				2
Вынесем из под корня k 0																						2		,
Вынесем из под корня k 0																								,


																																												2			n 2														2	n		2
																																																																2

											2												2 )																				k 02				1										k 02						3
							tg (				2					d			n 2											1													k 02														k 02												.
							tg (									d			n 2																																																		.
																		2			k 02														2												2														2
																					k 02										n 2				2												2				2										2						2
																																																n			2												n				2
																																																n			1												n			3
																														2					k 02										k 02						1							k 02								3
																																			k 02			1							k 02													k 02

																																																	n	2									2
																																																											2

																																																		2					k 02
																																																		2

Обозначим													0					. Тогда										отношение													d				станет
Обозначим							k 0											. Тогда										отношение												0					станет
							k 0																																	0

									d									1						arctg										1										2 n12																2 n 32								.
								0

															2 n 2					2													n 2		2											2 n						2									2 n					2
																		2												2									1													1													3
																																							1											n		2		2
																																																		n		2		2
																																																			2
		Отметим,															что				n-ая									мода								должна												удовлетворять																								условию:
n				d	( n 1) ,													где n=0,1,2.. .														Согласно этому условию отношение																																						d	для
n			2	d	( n 1) ,													где n=0,1,2.. .														Согласно этому условию отношение																																							для
			2																																																																								0
																																																																											0
волны Н0n определяется выражением:

	d				1									( n				arctg										1														2 n12											2 n 32																				),	(2.3.14 )
	0

		2				n 2 2																			n			2 2																				2				n					2					2 n 2
		2				n 2 2																			n			2 2																				2				n					2					2 n 2
					2																						2									n 2		2 (1																			1										3
																																				n 2		2 (1
																																		2																			n				2		2
																																																					n				2		2
																																																								2

где n=0,1,2…. соответствует локализованной ТЕ моде.

Волны типа Е0n

Для волн продольного электрического типа поперечные составляющие поля находятся из системы (2.3.3):

H х

j a

E z

(2.3.15)

E у

где Ez= A2 cos 2 y B 2 sin 2 y .

С учѐтом найденных продольных составляющих (2.3.2) уравнения,

определяющие структуру поля, записываются ниже:

Нх1=-j

а 1

A1е 1 у ,

Eу1=j

A1е 1 у ,

0 y

(2.3.16а)

Еz1 =A1е 1 у .

a 2

( A

sin

y B

cos

y )

х2

Еу2=

( A 2 sin

y B 2

cos 2 y ) ,

-d

y 0

(2.3.16б)

Еz2= A 2 cos 2

y B 2 sin

2 y .

Нх3=j	а 3			A3е 3 ( d у ) ,
Нх3=j				A3е 3 ( d у ) ,
		3
Eу3=-j			A3е 3 ( d у ) ,		-d y 0	(2.3.16в)
Eу3=-j		3	A3е 3 ( d у ) ,		-d y 0	(2.3.16в)
		3

Ez3=A3е 3 ( d у ) .

На основании граничных условий производим

определение констант: А1,

А2, В2, А3. Граничные условия имеют следующий вид:

Ez1=Ez2 и Hx1=Hx2

при

у =0 ,

Ez2=Ez3

Hx2=Hx3

при у=-d.

Откуда

1. А1=А2=С

(2.3.17а)

а 1

A1=

a 2

В 2

и В2=

а 1 2

С .

(2.3.17б)

а 2 1

C (cos 2 d

а 1 2

sin

2 d ) =А3 .

(2.3.17в)

а 2 1

а 2 3

(sin 2 d

а 1 2

cos 2 d ) =A3 .

(2.3.17г)

а 3 2

а 2 1

Дисперсионное уравнение получим, приравняв уравнения (2.3.17в) и (2.3.17г),

					cos 2 d	а 1 2			sin		2 d	=		а 2 3				(sin				2 d				а 1 2			cos		2 d ) .
					cos 2 d	а 2 1			sin		2 d	=						(sin				2 d				а 2 1			cos		2 d ) .
						а 2 1								а 3 2												а 2 1
																	(				а 1 3				)
																	(		1						)
													1						1			а 3
	Откуда:							tg ( 2 d )					1									а 3						.
	Откуда:							tg ( 2 d )							2	(	а 2			3		1		а 1			)	.
																	а 2			3		1		а 1
																	а 3 22							а 2
																	а 3 22							а 2
							1													1											1

Записав				1	( 2 k 2 n		2 ) 2 ,			2	( k	2 n			2	2 ) 2 ,							3	(				2 k	2 n		2 ) 2 , и обозначив
				1	0		1			2		0			2								3						0	3
		0	, получим отношение толщины пластины d																									к длине волны генератора
	k 0		, получим отношение толщины пластины d																									к длине волны генератора
	k 0

0 :

																								47
																	а 1
												2 n		2			а 1			2 n		2
d			1						1			2 n		1			а 3			2 n		3
														1								3
					( n	arctg																			) . (2.3.18)
0
													2 n		2			2			2
	2	n	2	2			n	2	2		а 2		2 n		2			2	n		2			а 1
			2					2			а 2				1						3			а 1
										а 3				n 22		2							а 2
										а 3				n 22		2							а 2

Мощность, переносимая по волноводу.

Данный оптический волновод предназначен для передачи мощности,

которая неравномерно распределена между тремя областями: I,II,III. В расчѐте предусмотрено сосредоточение основной части мощности в пленке (область II),

что подтверждается распределением поперечных составляющих электрического и магнитного полей Ех и Ну вдоль координаты у.

Исходными соотношениями являются: формула, определяющая среднее

значение вектора Пойнтинга П ср

, и выражение для расчета среднего

Re E H

значения мощности Р ср

П ср

ds .

Так как волновод не ограничен по оси X, мощность можно рассчитать на единицу длины по этому направлению. Тогда:

			0		d
Р срI	П срI dy ,	Р срII	П срII dy ,	Р срIII	П срIII dy .
	0		d

Общая мощность, канализируемая по волноводу равна :

III

Р I

Р II

Р III

Р I

ср

(2.3.19)

ср

Отношение

срII

Р срIII

показывает, как канализируемая мощность делится

Р срI

между областями.

Для вычисления мощностей Р I																		, Р		II		,	Р III		необходимо записать соответствующие
																	ср			ср				ср
значения векторов Пойнтинга:
		I	C 2 0								2		1	у															( 0 y )
	П	ср							e						,													при
	П	ср			2 12				e						,													при
					2 12
			C		2
			C					0											2
П	ср П срII							0	(sin					2		y			2	cos				2	y ) 2 ,			при	( d	y 0 ) .
П	ср П срII				2 22				(sin					2		y		1		cos				2	y ) 2 ,			при	( d	y 0 ) .
					2 22													1
				C	2		0					3									3
	П	III		C			0			(		3			sin			d			3			cos			d ) 2	e 2 3 ( d у ) , при	(	y d )
	П	ср				2 2				(					sin		2	d						cos		2	d ) 2	e 2 3 ( d у ) , при	(	y d )
		ср															2									2
													2									1
							3						2									1

Определим мощность, переносимую волной Н0m.

Мощность, канализируемая в области I

	C	2					C	2	a
	C	2			1 у		C		a
Р срI			a	e 2		dy					.	(2.3.20)
Р срI		2 12		e 2		dy		4		3	.	(2.3.20)
		2 12	0					4		3
										1

Мощность, канализируемая в области II.

Проведя расчет, получим

Р срII			П		срII	dy		C		2			a		(sin		2		y		2		cos		2 y ) 2 dy =
			0											0

			d							2 22				d							1
		2								2									2
	C								2						1			2								2
	C				0		(1		2		)		d		1	(1		2		) sin		2			d	2	(1 cos	2		d )	. (2.3.21)
				3			(1			2	)	2	d			(1			2	) sin		2		2	d		(1 cos	2	2	d )	. (2.3.21)
		4		3						2		2			2				2					2		1			2
		4		2						1					2				1							1

Мощность, канализируемая в области III.

Р срIII	C	2			3			3				e 3 ( d у ) dy
			0	(		sin	2 d		cos	2 d )
		4 32			2			1
											d

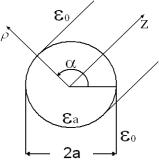
													49
=	C 2	0	(	3	sin			d	3	cos		d ) 2 .	(2.3.22)
=	4 33		(		sin		2	d		cos	2	d ) 2 .	(2.3.22)
							2		1		2
				2					1
2.4 Цилиндрический диэлектрический волновод
Круглый диэлектрический волновод (волоконный световод),													показанный
на рис.13, представляет из себя диэлектрический стержень													радиуса а с
диэлектрической проницаемостью a						и магнитной проницаемостью 0 . Обычно

он окружен воздухом.

Целью расчѐта является; решение дисперсионного уравнения, определение структуры поля и канализируемой по волноводу мощности, геометрических размеров (радиуса волновода) при заданном типе и длине волны,

диэлектрической проницаемости волновода.

Рис. 13 Геометрия круглого диэлектрического волновода Исходными данными для расчета являются частота f и тип поля: Еmn или

Нmn, где индекс m=0, а n задается. Рассмотрим решение для волн Н0n и E0n .

Порядок расчѐта:

1. На основании изложенной выше теории, при учѐте независимости полей

											50
от координаты		(		0 )		, записываются две частных и независимых системы:
от координаты		(		0 )		, записываются две частных и независимых системы:

E	j	0	Н z		,	H j		Н z		для волн типа Н0n ,	(2.4.1)
E	j	2			,	H j	2			для волн типа Н0n ,	(2.4.1)
		2					2
Н		а	dE z		,	Е j			Е z	для волн типа E0n .	( 2.4.2)
Н		2	d		,	Е j	2			для волн типа E0n .	( 2.4.2)
		2	d				2
2. Поперечные составляющие поля Е и										Н находим через продольную

составляющую поля Нz, для которой решаем волновое уравнение в цилиндрической системе координат:

2 Н z	1	H z	2 H		0 .	(2.4.3)
2				z

Это уравнение Бесселя и его общим решением является сумма двух функций:

функции Бесселя первого рода J0( ) и функции Бесселя второго рода - функции

Неймана N0( ) : Нz=AJ0( )+ВN0( ) .

3. Первым частным решением являются решения для области I ( 0 а ) в

котором удерживается только функция Бесселя первого рода			Нz1=AJ0( 1 ).
Функция второго рода (Неймана) исключается, так как при			0 она равна
N0(0)=	и решение при 0 принимает бесконечное	значение, что не

удовлетворяет требованиям теоремы единственности. Аргумент функции Бесселя

действителен, так как	1		k	2 n	2	2	- действительная величина.
	1			0	1

4.Вторым частным решением является решение для области II ( а ).

Вэтой области поле должно иметь поверхностный характер, так как аргумент

<<< < Предыдущая 1 2 3 45 / 125 6 7 8 9 10 11 12 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
05.02.20239.2 Mб14Распределенные сервис-ориентированные системы..pdf
#
05.02.2023283.13 Кб10Распространение лазерных пучков..pdf
#
05.02.20235.51 Mб87Распространение радиоволн и антенно-фидерные устройства..pdf
#
05.02.20231.52 Mб41Распространение радиоволн..pdf
#
05.02.2023425.46 Кб9Расчет деформационно-прочностных свойств композиционных материалов и напряженно-деформированного состояния простейших конструкций..pdf
#
05.02.20231.98 Mб28Расчет диэлектрических волноводов и объемных резонаторов..pdf
#
05.02.2023259.91 Кб13Расчет допусков и посадок сопрягаемых деталей..pdf
#
05.02.2023306.65 Кб18Расчет импульсной и переходной характеристик цепи..pdf
#
05.02.2023332.92 Кб31Расчёт надёжности функционального узла РЭС..pdf
#
05.02.20232.43 Mб9Расчет неуправляемого выпрямителя..pdf
#
05.02.2023131.15 Кб11Расчет переходных процессов классическим и операторным методами в цепях второго порядка..pdf