
Расчет диэлектрических волноводов и объемных резонаторов
..pdf
|
|
|
|
|
|
|
|
|
|
31 |
|
|
с 0 |
|
|
|
|
0 |
. |
|
(2.1.19) |
|
|
|
|
|
|
|
||||
|
|
|
|
|||||||
|
|
|
2 |
K з |
|
|
||||
|
f |
1 |
2 |
|
|
|
|
|
|
|
|
k 02 |
|
|
|
|
|||||
|
|
|
|
|
|
|
||||
Длина волны в волноводе изменяется от |
0 |
при |
2 =0 |
до =0 при 2 = . |
||||||
В первом случае волна должна рассматриваться как поперечная. Во втором прекращается еѐ распространение, так как коэффициент замедления становится равным бесконечности.
15. Групповая скорость.
Групповая скорость может быть определена из соотношения
v гр |
|
d |
|
|
1 |
|
|
|
|
|
|
|
|
при: |
|
|
0 ; |
|
0 . Откуда получим |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
d |
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 0 |
0 2 |
|
d 2 |
|
|
|
|
0 0 |
|
|
d 2 |
||||||||||||||||||
|
|
|
d |
|
d |
2 |
0 0 |
2 |
|
|
|
|
2 |
|
|
|
|
2 |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
d |
|
|
|
|
d |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
d |
|
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
0 0 |
|
|
|
|
|
|
|
|
0 0 |
2 |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 0 |
1 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
0 0 |
|
|
|
|
сK |
Э |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
(2.1.20) |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
v гр |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
2 |
|
|
|
d |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
|
0 |
|
0 |
|
|
|
d |
|
|
|
|
|
|
0 0 |
|
d |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
16.Мощность, канализируемая по волноводу.
Вдиэлектрическом волноводе мощность канализируется по двум областям:
I- внутри диэлектрического стержня, IIвне стержня.
Исходной формулой для расчета является среднее значение вектора Пойнтинга
|
|
1 |
|
|
|
|
* |
|
|
|
|
||||||
|
|
|
|
|
|
|||
П ср |
|
Re Е |
H |
. |
||||
|
||||||||
2
32
Например, для чѐтной волны электрического типа поперечные составляющие
записываются
E |
I |
j |
A |
cos |
|
|
y |
|
|||
y |
|
1 |
|
||||||||
|
|
|
|
1 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|||
H |
I |
|
j |
A a |
cos |
|
|
y |
|||
x |
|
1 |
|||||||||
|
|
|
|
1 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|||
, |
|
E |
II |
j |
C |
|
e 2 y , |
|
|
y |
|
||||||
|
|
|
|
|
2 |
|||
|
|
|
|
|
|
|||
, |
H |
II |
j |
C 0 |
e 2 y . |
|||
x |
|
|
||||||
|
|
|
|
2 |
||||
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
Е уI |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Е уII |
|
|
||
Для области I отношение |
|
|
|
|
|
|
. Для области II |
отношение |
|
|
|
|
. |
||||||||||||||||||||
|
|
Н хI |
а |
|
Н хII |
0 |
|||||||||||||||||||||||||||
|
|
|
|
|
A 2 |
|
|
|
|
|
|
|
|
|
|
|
A 2 r |
|
|
|
|
|
d ) e 2 2 |
у . |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
П II |
|
|
|
|
|
|
|
2 ( |
|
|
|
||||||||
|
П I k |
0 |
|
|
a |
cos 2 |
|
1 |
y , |
k |
0 |
|
a |
cos |
1 |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
ср |
|
2 2 |
|
|
|
|
|
|
|
ср |
|
|
|
2 2 |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
Средние мощности, |
канализируемые по областям |
равны: |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Р срI |
2 П срI |
dy |
|
и |
Р срII |
|
2 П срII |
dy . |
|
|
|
|
|
(2.1.21) |
||||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
Общая мощность, канализируемая по волноводу равна :
|
|
|
|
|
|
|
|
|
|
|
|
|
Р |
II |
|
|
|
|
|
|
Р |
|
Р I |
Р II |
Р I |
|
1 |
ср |
. |
||
|
|
|
|
|
ср |
|
|
||||||||
|
|
|
|
|
|
ср |
ср |
ср |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
Р |
I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
ср |
|
|
Отношение |
Р |
II |
/ Р |
I |
показывает отношение |
мощностей, канализируемых по |
|||||||||
|
|
ср |
|
ср |
|
|
|
|
|
|
|
|
|
|
|
областям.
17 . Затухание волн в диэлектрическом волноводе.
Затухание волн в волноводе происходит только в области I, так как во внешней области II диэлектриком является воздух.
Для первой области а является комплексной величиной

|
|
|
|
|
|
|
|
|
|
33 |
|
|
|
|
|
|
|
1 j tg |
|
|
|
|
|
|
|
|
|
|
|
1 tg 2 e j |
|
||||
|
|
|
|
а |
а |
a |
, |
||||
|
|
|
|
|
|
|
|
|
|||
где |
tg |
|
д |
- тангенс угла потерь диэлектрика. В этом случае постоянная |
|||||||
|
a |
||||||||||
|
|
|
|
|
|
|
|
|
|||
распространения тоже комплексная величина I I j |
. Здесь I - фазовая |
||||||||||
постоянная, - постоянная затухания.
В общем случае определение и осуществляется в соответствии с
теорией распространения волн в неограниченных средах с потерями. Векторы E
и |
|
пропорциональны е z e j t |
z . |
|
|
|
|
|
|
|
|
|
|
|
||||||
H |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
Для первой среды выражение для |
|
и I |
имеют вид |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a 0 |
|
|
1 , |
|
|
|
|
|
a 0 |
|
|
|
|
2 . |
||
|
|
|
1 tg 2 |
I |
|
|
2 |
1 tg |
2 1 |
|||||||||||
|
|
|
|
|||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Исходя из равенства постоянных распространения в первой и второй средах и (2.1.5), необходимо считать постоянную распространения во второй среде тоже
комплексной величиной II II |
j , для которой |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a 0 |
|
|
1 , |
|
|
0 0 |
|
|
|
|
2 . |
|||
|
1 tg 2 |
II |
2 |
1 tg |
2 1 |
|||||||||||
|
|
|||||||||||||||
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
2 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
18. Волновое сопротивление диэлектрического волновода.
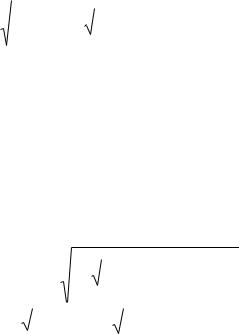
Волновым сопротивлением является отношение поперечных составляющих
электромагнитного поля. В первой среде для чѐтных волн это будет отношение:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
34 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a 0 |
|
|
|
1 2 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
I |
|
|
|
|
I |
|
|
|
2 |
1 tg |
2 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
I |
|
E y |
|
|
|
|
|
2 |
|
|
1 |
|
|
|
|
I |
|
j |
. |
(2.1.22) |
|||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
Z |
W |
H xI |
а |
|
|
|
|
|
а |
|
|
|
|
Z |
W |
e |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Здесь |
|
реальная |
|
часть |
|
|
комплексного |
волнового |
сопротивления |
равна |
||||||||||||||||||||||
Re Z I |
|
|
Z I |
|
сos |
, |
|
где |
|
- сдвиг фаз между поперечными составляющими |
||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||
W |
|
|
|
W |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
электромагнитного поля и
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
12 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
1 tg 2 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
I |
|
120 2 |
|
|
|
|
|
k |
2 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
||
|
Z |
W |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
||
|
|
r |
|
|
2 |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
1 tg |
|
|
|
II |
||||||||||||
Во второй среде |
|
для определения |
|
волнового сопротивления |
||||||||||||||||||
|
|
Z |
W |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
воспользуемся выражениями для поперечных составляющих (2.1.8а), где константу С необходимо выразить через константу A, используя граничные
условия E |
I E |
II |
|
, H |
I |
H II |
|
при y=d. |
|
Выражая |
C A sin( |
|
1 |
d ) e 2 d |
из первых |
|||||||||||||||||||||||||||||||||
|
|
z |
|
z |
|
|
|
|
x |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
уравнений системы (2.1.8а) и подставляя его в E |
II |
|
|
, а также из третьих уравнений - |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C A |
2 a |
cos( |
|
|
d ) e 2 d |
и подставляя в H |
II |
, получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
1 0 |
1 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
II |
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
y y |
|
|
II |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
y |
|
||||
|
|
|
jA |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
2 |
|
|||||||||||||||||||||||
|
|
E |
y |
|
|
sin( |
1 |
d ) e |
|
|
|
e |
|
|
, |
H |
x |
|
jA |
|
cos( |
1 |
d ) e |
|
e |
|
|
. |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Используя полученные выражения, определим волновое второй среды |
||||||||||||||||||||||||||||||||||||||||||||||||
сопротивление: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
II |
|
E yII |
|
|
|
|
1 |
|
|
|
|
|
|
I |
|
|
|
1 |
|
|
|
|
|
|
j |
|
|
. |
|
|
|
|
|
(2.1.23) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tg( |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
Z |
W |
|
|
|
|
|
|
|
|
|
|
|
tg |
1 |
d |
Z |
W |
|
|
|
|
|
1 |
d ) e |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
H xII |
a |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
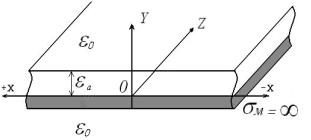
Суммарное волновое сопротивление диэлектрического волновода определим как
35
|
|
|
I |
|
II |
|
|
Z |
|
|
Z W |
Z W |
. |
||
|
|
|
|||||
W |
|
|
I |
|
II |
||
|
|
||||||
|
|
Z |
W |
Z |
W |
||
|
|
|
|
|
|||
2.2Планарный диэлектрический волновод.
Планарным диэлектрическим волноводом может служить металлическая плоскость, покрытая слоем диэлектрика с относительной диэлектрической проницаемостью r 1 (рис.11). Толщина слоя по оси Y равна d .
Рис. 11 Геометрия планарного диэлектрического волновода
В большинстве случаев окружающей средой является воздух. Под областью
I понимают область 0 у d |
, под областью II |
область |
d у . |
||||||||||
Волновые уравнения для продольных составляющих электромагнитных |
|||||||||||||
полей в первой среде в соответствии с (2.1.12) будут иметь обычный вид: |
|||||||||||||
|
d 2 E zI |
2 |
|
I |
|
|
d 2 Н zI |
|
2 |
I |
|||
|
|
|
1 |
E z |
, |
|
|
|
|
|
1 |
Н z . |
|
|
dy 2 |
|
dy |
2 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
||||
Решением этих уравнений являются: |
|
|
|
|
|
|
|
|
|||||
|
E I |
A sin |
|
1 |
y +Всos |
|
1 |
y , |
|
(2.2.1а) |
|||
|
z |
|
|
|
|
|
|
|
|
|
|||
|
H zI |
С sin |
1 y + Dсos 1 у . |
|
(2.2.1б) |
||||||||
В планарных волноводах должны удовлетворятся граничные условия при у=0 на
36
металлической поверхности: E zI 0 и H zI max .
Из рассмотрения этих уравнений следует, что для волн типа Е необходимо
оставить E zI A sin 1y , так как при этом выполняется граничное условие для
E |
I |
0 , а для волн типа |
Н необходимо оставить H |
I |
D cos |
у , так как при этом |
|
z |
|
|
z |
|
|
выполняется граничное условие - H zI max при у=0.
Во второй среде волны, как и в п.2.1, носят поверхностный характер.
Поэтому в дальнейшем будем использовать выражения (2.1.8).
Если по заданию требуется рассчитать волновод, вдоль которого должна распространяться волна тип Е, то для расчѐта таких волноводов используются формулы для чѐтных электрических волн:
|
I |
A sin |
1y |
|
, |
|
|
|
II |
Ce |
2 y |
, |
|
|
|
|
||||||||
E z |
|
|
|
|
E z |
|
|
|
|
|
|
|||||||||||||
|
I |
j |
A |
1 y |
|
, |
II |
j |
C |
|
2 |
y |
, |
(2.2.2) |
||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||
E y |
|
|
cos |
|
E y |
|
2 |
e |
|
|
||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
H |
I |
|
j |
A a |
cos |
|
|
y |
, |
H |
II |
|
j |
C |
0 |
e 2 y . |
|
|||||||
x |
|
|
|
|
1 |
x |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Если по волноводу должна распространяться волна типа Н, то следует использовать формулы для нечѐтных магнитных волн:
H |
I |
|
D cos |
1 |
y |
, |
H |
II |
Ce 2 y , |
|
|
|
||||||||||||
|
z |
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
||
H |
I |
|
j |
|
D |
|
sin |
|
|
1 y , |
H |
II |
j |
C |
e |
- |
2 y |
, |
|
(2.2.3) |
||||
|
|
|
|
|
|
|
|
|
||||||||||||||||
y |
|
1 |
|
|
|
y |
2 |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
I |
|
|
0 D |
|
|
|
1 y , |
|
II |
|
|
0 C |
|
|
- |
2 y |
. |
||||||
E x |
j |
|
|
|
|
sin |
E x |
j |
|
|
|
|
e |
|
|
|||||||||
1 |
|
2 |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
37
Таким образом, по такому волноводу могут распространяться только чѐтные электрические и нечѐтные магнитные волны.
Трансцендентные уравнения, предназначенные для определения поперечных волновых чисел и размера волновода имеют следующий вид:
|
0 |
( |
|
d ) tg |
|
d |
|
d |
- |
для волн чѐтного электрического типа, |
(2.2.4а) |
||
|
|
1 |
1 |
2 |
|||||||||
|
a |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
( 1 d ) ctg( |
1 d ) 2 d |
- |
для |
волн нечѐтного магнитного типа. |
(2.2.4б) |
|||||||
Дальнейшие расчѐты нужно |
проводить в соответствии аналогичными |
||||||||||||
расчѐтами, проводимыми в предыдущих параграфах.
2.3 Несимметричный диэлектрический волновод
Несимметричный диэлектрический волновод представляет из себя
диэлектрическую пластину, имеющую размер |
d в направлении одной из |
||||
поперечных |
осей, в данном случае у, и |
обладающую |
абсолютной |
||
диэлектрической проницаемостью а 2 (рис.12). |
|
|
|
|
|
При у=0 она граничит с диэлектриком, |
простирающимся |
до |
у= |
и |
|
обладающим |
абсолютной диэлектрической проницаемостью а 1 . |
При |
у |
d |
|
пластина граничит с диэлектриком, обладающим абсолютной диэлектрической
проницаемостью а 3 и простирающимся до |
у= . |
|
Предполагается, что а 2 а 1 и |
а 2 а 3 . |
|
Таким образом всѐ пространство делится на три области:
I. 0 у , имеющей абсолютной диэлектрическую проницаемостью а 1 ,

38
II. 0 y d, имеющей абсолютной диэлектрическую проницаемостью а 2 , III. -d у , имеющей абсолютной диэлектрическую проницаемостью а 3 .
Следовательно, показатели преломления диэлектриков данной структуры зависят
только от направления у и равны: n1= 
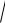 r 1 , n2=
r 1 , n2= 
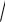 r 2 , n3=
r 2 , n3= 
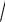 r 3 .
r 3 .
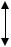 d
d
Рис. 12 Геометрия несимметричного диэлектрического волновода
Так как несимметричный диэлектрический волновод имеет три области с различными диэлектрическими проницаемостями, необходимо решать три волновых уравнения для продольных составляющих Еz и Нz, соответствующих
областям: I,II,III. Если ввести |
|
Е z |
|
( у ) |
, то |
||
|
|
|
|
|
|
||
|
|
||||||
|
|
|
H z |
|
( у ) |
|
|
d 2 1 |
|
|
2 |
|
0 |
|
|
|
|
|
1 |
||
|
dу 2 |
1 |
|
|||
|
|
|
|
|||
|
d 2 2 |
2 |
|
0 |
||
|
|
|
|
2 |
||
|
dу 2 |
2 |
|
|||
|
|
|
|
|||
d 2 3 |
|
2 |
|
0 |
||
|
|
|
|
3 |
||
|
dу 2 |
3 |
|
|||
|
|
|
|
|||
вобласти I, где
вобласти II, где
вобласти III, где
12 k 02 n12 2
22 k 02 n 22 2
32 k 02 n 32 2
, (2.3.1а)
, (2.3.1б)
. (2.3.1в)
В данных формулах k 0 
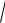 0 0 - постоянная распространения
0 0 - постоянная распространения
свободного воздушного пространства, постоянная распространения волны в

39
волноводе, а 1 , 2 , 3 -поперечные постоянные распространения для первой,
второй и третьей областей соответственно.
Согласно изложенной выше методики расчѐта диэлектрических волноводов, следует искать выражения для Еz и Нz в каждой отдельной области,
затем выразить через них поперечные составляющие и используя граничные условия (приравнивая тангенциальные составляющие на границе раздела),
определять неизвестные константы и записать дисперсионные уравнения.
Общее решение волнового уравнения для волны, бегущей вдоль оси z, имеет вид
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Е z ( у ) |
exp j |
y . |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1, 2 , 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H z ( у ) |
|
|
|
|
|
|
|
|
|
||||||
Tак как для первой и третьей областей |
|
k 2 n 2 |
2 |
и k |
2 n |
2 2 отрицательны, то |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
|
|
0 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
1 |
j |
2 k |
2 n |
2 и |
3 |
j |
2 k |
2 n |
2 |
, |
и |
решение для этих областей будет |
|||||||||||||||||||
|
|
|
|
0 |
1 |
|
|
|
|
|
|
|
|
0 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
||||
представлено |
в |
виде |
затухающих |
экспонент: exp( 1 y ) |
при 0 y |
и |
||||||||||||||||||||||||||
exp( |
3 y ) |
при |
y d . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Для второй области разность |
k 2 n |
|
2 2 |
|
|
положительна и решение будет иметь |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вид |
exp( |
j 2 y ) |
или |
|
|
A 2 |
cos |
2 |
y B 2 |
sin |
2 y . |
|
|
|
|
|
|
|
||||||||||||||
Следовательно: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А1 ехр(- 1 у ) , |
при |
|
0 y |
, |
( 2.3.2а) |
||||||||||||
|
|
|
|
|
|
|
Е z |
|
|
( у ) |
|
|
|
|
|
|
|
|
|
|
|
y , |
при |
-d y 0 |
, |
( 2.3.2б) |
||||||
|
|
|
|
1, 2 , 3 |
|
|
|
|
|
|
|
A 2 |
cos |
2 |
y B 2 |
sin 2 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
H z |
|
|
( у ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А3 ехр( 3 ( d у ) ) , |
при |
y d . |
( 2.3.2в) |
||||||||||||||
Поперечные составляющие для волн типа Еmn и |
Нmn найдѐм из системы |
40
уравнений (1.8):
|
2 |
H |
|
j |
|
|
E z |
, |
2 E |
|
j |
|
E z |
, |
|
||||||||
|
x |
a |
|
|
|
|
|
у |
|
|
|||||||||||||
|
|
|
|
|
у |
|
|
|
|
|
|
|
у |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( 2.3.3) |
||||
|
|
|
|
|
|
H |
|
|
|
|
|
|
|
|
|
H |
|
|
|
||||
|
|
2 |
E |
х j 0 |
z |
, |
|
|
2 |
H у |
j |
z |
|
. |
|
||||||||
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
у |
|
|
|
|
|
у |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Волны типа Н0m. Поперечные составляющие поля находятся из системы (2.3.3)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
E х |
|
j |
|
H z |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
у |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
H у |
|
j |
z |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
у |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ну1=j |
|
|
|
|
A1е 1 у , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Eх1=j |
0 |
|
|
A1е 1 у |
|
, |
|
|
область I |
|
|
0 у |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Hz1 = A1е |
|
1 |
у |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Hу2= |
|
|
|
( A 2 sin 2 |
y B 2 |
|
|
|
2 y ), |
|
|
|
|
|
|
|
|||||||||||||||||
j |
|
|
cos |
|
|
|
|
|
|
|
|||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Е |
= |
j |
0 |
|
( |
A |
|
|
sin |
|
y B |
|
cos |
|
|
y ) , |
|
область II |
-d y 0 |
||||||||||||||
|
|
|
|
|
2 |
|
2 |
2 |
2 |
|
|||||||||||||||||||||||
х2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Hz2= A 2 cos |
2 |
y B 2 |
|
sin 2 y . |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Ну3=-jA3 |
|
|
|
e |
3 ( d у ) |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Eх3=-j |
0 |
|
|
A3е 3 ( d у ) |
, |
|
|
|
|
область III |
- |
y 0 |
|||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Hz3=A3е 3 ( d у ) .
(2.3.4)
(2.3.5а)
(2.3.5б)
(2.3.5в)
