
Расчет диэлектрических волноводов и объемных резонаторов
..pdf
|
|
2 E zII |
|
|
|
2 E zII |
|
|
|
|
|
|
2 E |
II |
, |
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
. |
|
|||||||||||||||||||
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
y 2 |
|
|
|
z 2 |
|
|
0 |
z |
|
|
|
|
|
|
0 |
|
|
|
0 |
0 |
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
3. Так как Еz e j t z |
, перепишем волновые уравнения, заменив |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
2 |
E |
I |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
I |
|
|
|
|
|
2 |
I |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
z |
2 |
|
|
|
, |
|
|
|
|
|
|
y |
2 |
|
|
|
k |
|
|
|
|
E z |
1 |
|
E z |
, |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
2 E zII |
k |
|
2 |
|
2 E |
|
II |
|
|
2 E |
II . |
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
z |
2 |
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
y 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Здесь |
|
|
|
1 |
= k |
0 |
|
r |
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
2 |
= k 0 |
|
|
|
= |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
- квадраты поперечных волновых чисел для области I и области II.
21
(2.1.1б)
(2.1.2а)
(2.1.2б)
(2.1.3а)
(2.1.3б)
|
Для |
выполнения |
условия |
|
c |
|
1 |
|
|
ф |
c 0 |
|
1 |
|
|
постоянная |
||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||
|
0 a |
0 0 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
распространения |
|
должна |
быть |
|
действительным |
числом, причѐм должны |
||||||||||||||||
выполняться неравенство k 0 r |
|
k 0 , из которого следуют равенства: |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
1 |
|
k 0 r |
2 |
и |
2 j |
|
2 k 02 |
|
, причѐм 1 |
действительное |
число, а 2 - |
|||||||||||
мнимое. Вследствие этого, волновое уравнение для первой области не изменится,
т.е. будет иметь прежний вид
2 E zI |
|
|
2 E |
I . |
(2.1.4а) |
|
1 |
||||
y 2 |
|
|
z |
|
|
|
|
|
|
|
Для второй области

|
|
|
|
|
|
|
|
|
|
|
22 |
|
|
2 E zII |
|
2 k |
|
2 E II |
|
2 E |
II . |
(2.1.4б) |
|
|
|
|
|
0 |
|||||||
|
|
y 2 |
|
|
z |
|
2 |
z |
|
||
|
|
|
|
|
|
|
|
|
|
||
Продольная постоянная распространения одновременно равна |
|
||||||||||
|
|
|
|
|
|
|
|
|
|||
= |
k 02 r |
12 |
и |
|
= |
k 02 22 |
. |
(2.1.5) |
|||
4. Запишем в соответствии с |
(1.8) выражения |
для поперечных составляющих |
|||||||||
поля в первой и второй областях: |
|
|
|
|
|
|
|
||||
|
E |
I |
|
|
j E zI |
e |
j Z |
|||||||
|
y |
1 |
2 |
|
|
y |
|
|||||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||||
E |
II |
|
|
|
|
j E zII |
e |
j Z |
||||||
y |
|
2 |
2 |
|
|
|
|
y |
|
|||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||
,
,
H |
I |
j |
a |
|
E zI |
|
e j Z , |
||||
x |
|
|
|
|
y |
||||||
|
|
|
1 |
2 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
||||
H |
II |
j |
0 |
|
E zII |
|
e j Z . |
||||
x |
|
|
|
||||||||
|
|
|
|
2 |
|
|
y |
|
|
||
|
|
|
|
2 |
|
|
|
|
|||
5. Решения волнового уравнения для области I и II хорошо известны и имеют вид:
для области I |
E |
I A sin |
|
1 |
y |
B cos |
|
1 |
y , |
|
(2.1.6а) |
|||||
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
||
для области II |
|
II |
|
|
2 y |
|
De |
|
|
y |
. |
(2.1.6б) |
||||
|
E z |
Ce |
|
|
|
2 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6. Решение (2.1.6а) состоит из суммы двух частных, независимых решений: |
||||||||||||||||
|
|
|
E |
I |
A sin |
|
1 |
y |
|
, |
|
|
|
(2.1.7а) |
||
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
I |
B cos |
|
1 |
y |
|
|
. |
|
(2.1.7б) |
|||
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
Каждое из этих решений соответствует самостоятельной электромагнитной волне, распространяющейся вдоль пластины: (a) соответствует электрической четной волне, (б) - электрической нечетной волне. Название этих волн связано с
тем, что в первом случае составляющим поля E yI и H xI , определяющим вектор
Пойнтинга, направленный вдоль оси Z , соответствует закон cos 1 у, т.е. четный
|
|
|
|
|
|
|
|
|
23 |
относительно |
y 0 |
, а во втором нечетный - sin 1 у . |
|||||||
7. Решение |
II |
Ce |
|
2 |
y |
De |
2 |
y |
нужно подчинить требованиям теоремы |
E z |
|
|
|
|
|
||||
единственности, для чего из него необходимо исключить второе слагаемое,
положив константу D 0 , так как функция e 2 y при y |
равна бесконечности. |
||
Следовательно, в решении остаѐтся только одно слагаемое |
- E |
II |
Ce 2 y . |
|
|
z |
|
8. Пользуясь формулами (2.1.6), записываем выражение для составляющих поля
волны |
Е 0 n |
в первой и второй средах для четных и нечетных волн: |
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- для четных волн. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
I |
A sin |
1 y |
|
, |
|
|
II |
Ce |
2 |
y |
, |
|
|
|
|||||||||||||||||||
|
|
|
|
|
E z |
|
|
E z |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
I |
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
, |
II |
|
|
|
|
C |
2 y |
, |
|
(2.1.8а) |
||||||||||||
|
|
|
j |
|
|
|
cos 1 y |
|
|
j |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
E y |
|
|
|
|
|
|
E y |
|
|
|
|
|
e |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||||||
|
|
H |
I |
|
j |
A a |
|
cos |
|
|
|
y |
, |
H |
|
II |
|
j |
C 0 |
|
|
e 2 y |
, |
|
|||||||||||||||
|
|
x |
|
|
|
1 |
|
|
1 |
x |
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
- для нечетных волн |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
E |
I |
|
A cos |
|
|
1 |
y |
, |
|
|
|
|
|
E |
II |
Ce 2 y , |
|
|
|
||||||||||||||||
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
I |
|
|
|
j |
|
A |
sin |
|
|
y |
|
, |
|
|
E |
II |
|
|
j |
C |
e 2 y |
, |
(2.1.8б) |
|||||||||||||
|
|
y |
|
|
|
|
|
1 |
|
|
|
y |
|
2 |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
H I |
j |
|
A a |
sin |
|
|
|
y |
|
, |
H |
|
II |
j |
C |
0 |
e 2 y . |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
x |
|
|
|
|||||||||||||||||||||
|
|
x |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Эти |
уравнения |
|
в |
|
дальнейшем |
будем |
|
использовать |
для |
построения |
|||||||||||||||||||||||||||||
структуры поля, но прежде нужно определить поперечные постоянные распространения 1 и 2 .
24
9. Вывод уравнений, предназначенных для определения поперечных волновых чисел 1 и 2 .
Для вывода этих уравнений используются граничные условия на границе
диэлектрик-диэлектрик: E 1 E 2 и H 1 H 2 при y d .
Для случая электрических четных волн граничные условия записываем
|
|
E |
I |
E |
II |
и |
|
H |
I |
H |
II |
, |
|
|
|
|
|
z |
|
z |
|
|
|
x |
|
x |
|
|
|
или |
A sin 1 d |
Cе 2 d |
и |
|
j |
A |
a |
cos |
1 d |
|
j |
C 0 |
e 2 d . |
|
|
1 |
|
2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Разделив почленно первое уравнение на второе, произведя необходимые сокращения и домножив левую и правую части на d, получим:
для четных волн |
1 d |
1 |
|
tg |
1 d |
2 d , |
(2.1.9 а ) |
||
|
r |
||||||||
|
|
|
|
|
|
|
|||
для нечетных волн |
1 d |
1 |
|
ctg |
1 d |
2 d . |
(2.1.9б) |
||
r |
|||||||||
|
|
|
|
|
|
||||
10. Волны магнитного типа |
H 0 n |
|
|
|
|
|
|
|
|
Как и в случае электрических волн запишем выражения для продольных составляющих магнитного поля.
для области I |
|
|
H |
I |
A sin |
|
1 |
y , |
|
(четные волны) |
( 2.1.10а) |
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
H |
I |
B cos |
|
1 |
y |
, |
(нечетные волны) |
(2.1.10б) |
|
|
|
|
z |
|
|
|
|
|
|
|
для области II |
H |
II |
Ce 2 y , |
для чѐтных и нечѐтных волн . |
(2.1.11) |
||||||
|
|
z |
|
|
|
|
|
|
|
|
|
Переход от продольных составляющих к поперечным осуществляется с помощью формул:
H |
I |
j |
|
|
|
H zI |
|
|
y |
1 |
2 |
|
y |
|
|||
|
|
|
|
|
|
|||
H |
II |
j |
|
|
|
|
H zII |
|
y |
|
2 |
2 |
|
y |
|
||
|
|
|
|
|
||||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
||
,
,
E |
I |
j |
0 |
|
H zI |
||||||
x |
|
|
|
y |
|||||||
|
|
|
|
1 |
2 |
|
|
|
|||
|
|
|
|
|
|
|
|
||||
E |
II |
j |
0 |
|
H zII |
|
|||||
x |
|
|
|
||||||||
|
|
2 |
|
|
|
y |
|||||
|
|
|
|
2 |
|
|
|
|
|||
25
,( 2.1.12а)
. ( 2.1.12б)
После подстановки |
H |
|
I |
|
и |
|
H |
II |
получаем выражения, |
определяющие |
||||||||||||||
|
|
|
|
z |
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
||
структуру электромагнитных полей магнитного типа. |
|
|
|
|
||||||||||||||||||||
Для четных волн: |
H I A sin |
|
1 |
y |
, |
|
|
H |
II |
Ce 2 y |
, |
|
||||||||||||
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
||
H yI j |
|
|
A cos |
1 y |
, |
H yII |
j |
|
|
C e - 2 y , |
(2.1.13а) |
|||||||||||||
|
|
|
|
|
||||||||||||||||||||
1 |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||||
E I |
j |
0 |
|
A cos |
|
|
y |
, |
E I |
j |
0 |
|
C e - 2 y . |
|
||||||||||
|
|
|
|
1 |
|
|
||||||||||||||||||
x |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
x |
|
|
2 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Для нечетных волн: |
H I B cos |
|
1 |
y |
|
, |
|
H |
II |
Ce 2 y |
, |
|
||||||||||||
|
z |
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|||
H |
I |
|
j |
|
|
B sin |
|
|
|
y |
|||
y |
1 |
1 |
|||||||||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||
E |
I |
|
j |
0 |
|
B sin |
|
|
|
y |
|||
x |
1 |
|
1 |
||||||||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||
,
,
|
II |
|
|
|
|
|
- |
2 y |
|
||
H |
j |
|
|
C e |
|
||||||
y |
|
|
|
|
|
|
|||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
II |
|
|
0 |
|
|
- |
2 y |
|||
E x |
j |
|
2 |
C e |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||
, (2.1.13б)
.
|
Уравнения для определений |
поперечных |
постоянных |
распространения |
|
1 |
и 2 и толщины диэлектрической пластины |
d имеют вид: |
|
||
|
для четных волн |
1 d tg( |
1 d ) 2 d , |
(2.1.14а ) |
|
|
для нечетных волн |
1 d ctg( |
1 d ) 2 d . |
( 2.1.14б) |
|
11.Решение трансцендентных уравнений.
Трансцендентные уравнения для волн типа Е, в которые входят
неизвестные поперечные волновые числа 1 |
и 2 , удобнее всего решать |
26
графическим методом.
Но прежде чем преступить к построению графиков следует вывести еще одно уравнение, так как число уравнений должно быть равно числу неизвестных.
Исходя из того, что продольная постоянная распространения для I и II сред одинакова, мы можем записать равенство:
|
k 22 |
|
2 |
|
k12 |
|
|
|
2 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
2 |
|
1 |
здесь |
k 1 |
|
|
0 а , |
k 2 |
0 0 , |
|
|||||||||||||||
откуда 2 |
2 |
k 2 |
k 2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1 |
2 |
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Помножив левую или правую часть уравнения на d 2 получим: |
|
|
|
|||||||||||||||||||||||
|
|
|
( |
1 |
d ) 2 ( |
2 |
d ) 2 |
d 2 |
k 2 |
k |
2 |
= R 2 . |
|
|
|
(2.1.15) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|||
Это уравнение |
является |
уравнением окружности в координатах 2 d |
и 1 d, |
|||||||||||||||||||||||
радиус которой: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
2 |
|
|
2 d |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
R |
d |
|
k |
|
k |
k |
0 |
|
|
r |
1 . |
|
|
|
(2.1.16) |
||||||||
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
В координатах 1 d и 2 d могут быть построены и графики функций, входящих
в трансцендентные уравнения (2.14а), (2.14б). Точки пересечения окружности и соответствующих трансцендентных функций позволяют определить 1 d и 2 d.
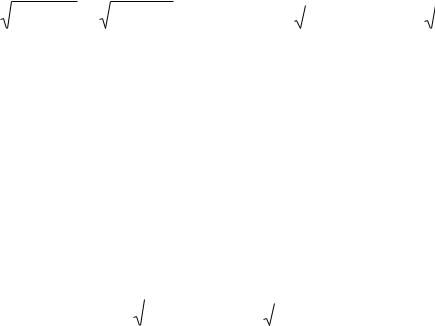
12. Рассмотрим построение графиков для четных электрических волн, для которых дисперсионное уравнение - ( 1 d ) tg( 1 d ) r 2 d .
Отложим по оси абсцисс 1 d в радианах, а по оси ординат |
2 |
d = |
1 |
tg ( 1 d). |
|
r |
|||||
|
|
|
|
27
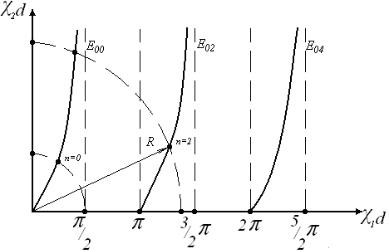
Рис. 8 Графическое решение дисперсионного уравнения для волн четного типа.
Необходимо помнить, что 1 d и 2 d должны быть положительными, так
как в противном случае могут быть нарушены требования теоремы единственности. После построения графиков функций (рис.8), проведѐм в этих
же координатах окружность радиуса R. |
|
|
Точки пересечения окружности с кривыми определяют |
решение |
|
трансцендентного уравнения и, следовательно, определяют рабочие точки. |
||
Опустив из этих точек перпендикуляры на оси 1 d |
и 2 d, определим их |
|
значения, а следовательно, при известной толщине d и значения 1 , |
2 . Индекс n |
|
определяет тип волны распространяющейся по волноводу. От него зависит количество вариации поля по оси y.
Пересечение окружности c первой тангенсоидой соответствует n=0, т.е.
волне Е 00 |
, со второй n=2 волне Е 02 , с третьей n=4 волне Е 04 и т.д.. Таким |
образом, |
для чѐтных волн могут существовать волны: Е 00 , Е 02 , Е 04 и так далее. |
На рис.9 изображены графики для нечѐтных волн, соответствующие
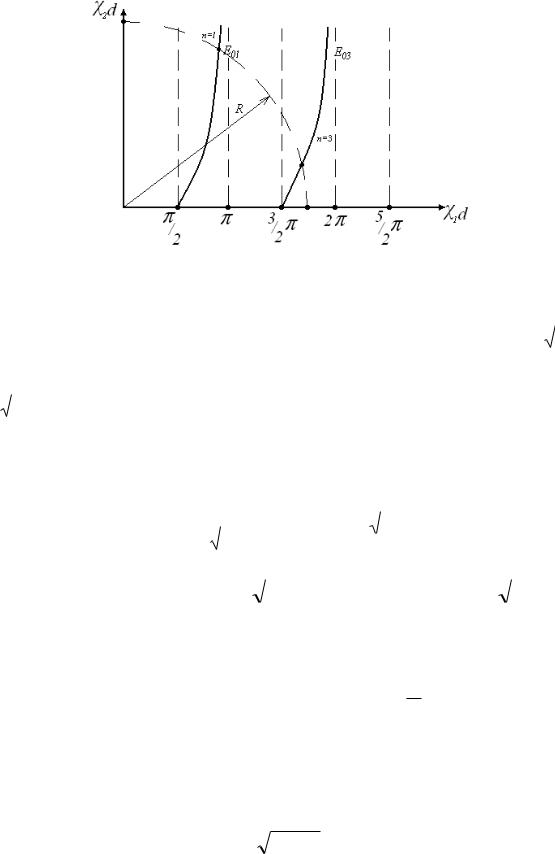
28
дисперсионному уравнению 1 d |
1 |
ctg 1 d |
2 d . |
|
|||
|
r |
|
|
Рис. 9 Графическое решение дисперсионного уравнения для волн нечетного типа
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||||||||||||||||
|
Так |
как согласно формуле |
(2.16) |
радиус |
окружности |
R =d |
|
|
r |
1 = |
|||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 f |
|
|
, то условием существования волн чѐтного типа Е0n будет R >n |
|
(где |
|||||||||||||||||||||||||||||||||
d |
|
r 1 |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
c 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
n=0,2,4,..) с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
с |
0 n |
|
|
1 |
|
|
|
|
|
|
|
4 d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f кр |
|
|
|
|
|
|
|
и |
кр |
|
|
r |
1 . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
4 d |
|
|
r |
1 |
n |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Так для волны типа |
E |
02 |
|
|
кр |
|
2 d |
r |
1 , |
для |
E |
04 |
|
|
кр |
d |
|
r |
1 |
и так |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
далее. Из диаграммы типов колебаний (рис.9) следует, что условием
существования волн Е 0 n нечѐтного типа является R n , где n=1,3,5… .
2
Следовательно, критическая длина волны для волн чѐтного и нечѐтного
типов определяется общей формулой:
кр |
|
4 d |
r |
1 |
, при этом n=1,2,3,4,5…. (2.1.17) |
|
n |
|
|||
|
|
|
|
|
29
Откуда следует, что волна типа E 01 имеет самую большую критическую длину
волны для рассматриваемого волновода равную Е 01 кр |
|
|
|
|
||
4 d |
r |
1 . Следом |
||||
за ней идѐт Е 02 кр 2 d |
|
|
|
|
|
|
r 1 и так далее. |
|
|
|
|
||
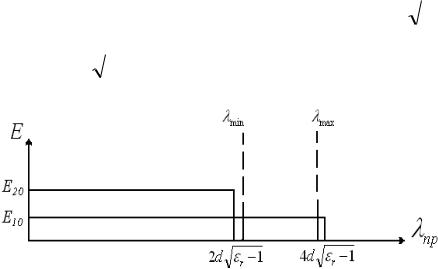
Рис. 10 Диаграмма типов колебаний Диапазон длин волн может быть рассчитан по аналогии с металлическими
волноводами: |
max |
0 ,8 Е 01 кр , |
|
min |
1, 2 Е 02 |
кр (рис.10). |
|
|
|
|
|
Из графиков (рис.8) видно, что волна четного типа E 00 может существовать при любом значении R, так как для неѐ имеются точки пересечения в интервале
от 1 d 0 до 1 d .
Но если потребовать, чтобы в волноводе распространялась только волна
E 00 , то 1 d должна лежать в пределах |
0 |
|
. Как видно из графиков рис.8, |
2 d |
||||
|
||||||||
|
|
|
|
|
2 |
|
|
|
при этом тоже мало. |
|
|
|
|
|
|
|
|
При малом 2 функция |
e |
|
2 |
y |
убывает медленно. Это означает, |
что |
||
|
|
|
||||||
значительная часть мощности в этом случае распространяется в воздухе. При
|
1 |
=0 и |
2 |
=0, поле вырождается: |
E |
I |
B , |
E |
I |
E |
II |
0 . |
|
|
|
|
z |
|
|
x |
|
y |
|
Для волны E 00 , кр , при этом волновод теряет свои направляющие

30
свойства и поле приобретает характер поперечной волны, излученной возбуждающей системой в свободное пространство.
В диэлектрическом волноводе, также как и в металлических волноводах,
существует дисперсия, т.е. частотная зависимость основных параметров волновода, в том числе длины волны в волноводе, от частоты.
13. Фазовая скорость и коэффициент замедления поверхностных волн
Фазовая скорость определяется известным соотношением - v ф |
|
|
. |
||||||||||||||||||||||
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Откуда , с учѐтом |
= |
k |
2 |
|
2 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
0 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v ф |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
с 0 |
|
|
|
. |
(2.1.18) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
2 |
0 0 |
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
k 02 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Из этого соотношения следует, что волна в диэлектрическом волноводе распространяется со скоростью меньше скорости света с 0 .
При 2 =0 фазовая скорость равна скорости света, при 2 |
|
v ф 0 . |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
Знаменатель (2.1.18) представляют в виде |
1 |
2 |
|
|
K з |
, при этом K з |
называют |
|||
|
|
|
|
|||||||
k 02
коэффициентом замедления.
14. Длина волны в волноводе.
Длина волны в волноводе определяется формулой v , или с учетом (2.1.18)
f
