Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Томский Государственный Университет Систем Управления и Радиоэлектроники

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Расчет диэлектрических волноводов и объемных резонаторов

..pdf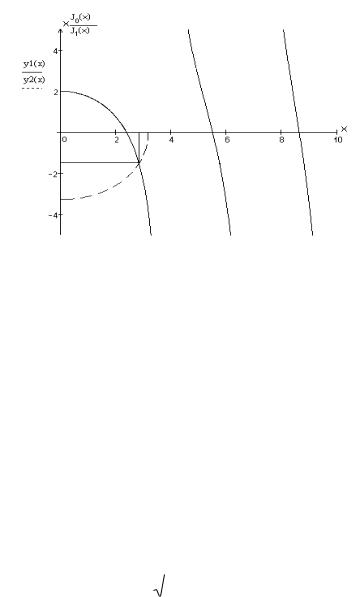

Скачиваний:

Добавлен:

05.02.2023

Размер:

1.98 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 1210 11 12 > Следующая >>>

								91
1 a	J	0	( 1 a )	2 a	K 0	( 2 a )	.	(4.3.7)
1 a	J 1 ( 1 a )			2 a	K 1 ( 2 a )		.	(4.3.7)
	J 1 ( 1 a )				K 1 ( 2 a )

5. Графическое решение дисперсионного уравнения, построение графиков.

Левая часть дисперсионного уравнения - функция	y1 ( x )		x	J 0	( x )	, где
				J 1	( x )

x 1 a . Построим график зависимости этой функции (рис.26)		от		аргумента
x 1 а , который откладываем по оси абсцисс, и график функции		y 2 ( x ) R .

Рис. 26 Графическое решение дисперсионного уравнения

Точки пересечения функций y 1 ( x ) и y 2 ( x ) определяют рабочую точку для заданного типа колебаний.

6. Определение поперечных волновых чисел

Для определения поперечных волновых чисел 1 , 2 на графике проведѐм

окружность радиуса R		(больше 01		2 , 405 и меньше 3,832) с центром в начале
			2 a
координат,	например, R				r	1 =3. Из точки пересечения проводим



перпендикуляры на оси		1 а и 2 а . Получим					1 а 2 ,6 ,	2 а 1,66 .

Откуда		2 .6	,		1 .66	.
	1			2
		а			а

7. Определение радиуса диэлектрического стержня.

Используя соотношение (2.4.9), получим

	а		0 n			с			0 n			.
			0 ,8						1,6
											r 1 1
						r 1 1					r 1 1
В	нашем				примере				заданы:				0 .63	мкм , r 1	2 .25 , волна Н 01 . Поэтому
01	2 , 405			и
	а	2 ,05		0 ,63				0 , 268		мкм.


		1,6		2 , 25			1

На практике рекомендуется выбирать a несколько больше рассчитанного, при этом удовлетворяя условию существования выбранного типа колебаний.

9. Уравнения, определяющие структуру поля.

0 а

2 .6

0 а

1 .66

)

J (

)

K (

2 .6

z 0 1

1 .66

z 0

2 .6

1 .66

z 0

(

)

для обл.I. H

H z 0

(

) для обл.II.

2 .6

1 .66

2 .6

1 .66

Z 0 J 0

(

)

H z 0 K 0

(

)

10. Проверка граничных условий:

Граничные

условия:

= H

при

выполняется при

= H

J 0

( 1 а )

а равенство Е

при а

требует

равенства

z 0

(

а )

																		1 a			J 0 ( 1 a )								2 a			K 0 ( 2 a )	.
																		1 a			J 1 ( 1 a )								2 a			K 1 ( 2 a )	.
																					J 1 ( 1 a )											K 1 ( 2 a )
При			а			J 0		( 2 ,6 ) -0,23 ,									J 1 ( 2 ,6 ) = 0,46,										K 0 (1,66 ) =0,17, K 1 (1,66 ) =0,22,
следовательно: 1 a												J 0 ( 1 a )					=1,3					2 a		K	0	( 2 a )					=1,28.
следовательно: 1 a												J 1 ( 1 a )					=1,3					2 a		K 1 ( 2 a )							=1,28.
												J 1 ( 1 a )												K 1 ( 2 a )
11. Проверка равенства постоянных распространения для I и II областей.

				2							2		или								2									2 .
				2		0	0			2	2		или								2		0		а				1	2 .

														2				( 2 .6 0 .63 ) 2										2
		2			1 (			2		)	2			2		1		( 2 .6 0 .63 ) 2										2				1 .39 ,
					1 (			2 а		)						1		( 2			0 .268				) 2							1 .39 ,
																			2
	2				2 .25 (				1 .66 0 .63						) 2				2	1 .38 .
					2 .25 (										) 2					1 .38 .
									2			0 .268

Так как граничные условия выполняются и постоянная распространения одинакова для обеих областей, математические вычисления проведены правильно.

12. Мощность, канализируемая по круглому волноводу.

Как и в случае прямоугольного диэлектрического волновода, мощность

канализируется по двум областям: в области I ( 0 а ) - Р ср и в области II

( а ) - Р ср .

Для определения средней мощности используем формулу Р ср П ср dS ,

dS= .

Запишем выражения для средней мощности через Нz для волн типа Н

															2		I														1			2		II
							Р срIH 1										Z W			Н zI		2	ds ,					Р срIIH			1				Z W				Н zII		ds ,
																						2																			2

												2			12																2			22
												2			12				S												2			22				S
																								а										а	2							1			m	2
Учитывая выражение для интеграла																									J m2		( ) d							а		J m2 ( )						1		( а 2	m		) J m2 ( )
Учитывая выражение для интеграла																									J m2		( ) d									J m2 ( )								( а 2		2	) J m2 ( )
																								0										2						2
[2], для поля, не зависящего от , получим:
			1 2 2 Z I											a												1			2 Z I	a 2
Р срIH							W	( Н zI 0 ) 2 J 02 ( 1 ) d																					W			( Н zI 0 )					2 ( J 0 2 ( 1 а ) J 02 ( 1 а )) =
Р срIH					12			( Н zI 0 ) 2 J 02 ( 1 ) d																						2		( Н zI 0 )					2 ( J 0 2 ( 1 а ) J 02 ( 1 а )) =
		2			12								0												2				1
	=	1 2 Z I				a 2					I	) 2 (J					2 (		а ) J 2						а )) ,
					W				( Н		I												(
									( Н		z 0							1					(	1
		2				2					z 0					1		1				0		1
		2				2
					1
				2		II									a														2	II	2
			1		Z W 2										a												1		Z W a
Р IIН			1		Z W 2				( Н		II		) 2				K 2	(			) d				=		1		Z W a				( Н			II	) 2 ( K 2			(				а ) K 2		(			а )) ,
Р IIН									( Н				) 2				K 2	(			) d				=								( Н				) 2 ( K 2			(				а ) K 2		(			а )) ,
ср		2				2					z 0				0		0			2							2		22							Z 0	0						2	0				2
						2
где	Z I		Z II				0			.
где	Z I		Z II							.
	W			W

Подставляя численные значения, получим

= P

+ P

IIH

= P

(( 0 , 445 2 0 , 24 2 ) / 2 ,6 2

0 , 24

( 0 , 22

2 0 ,17

2 ))

0 ,192 P

ср

0 , 445

1,66 2

где

2 Z WII

a 4

( Н

) 2 .

ср

Z 0

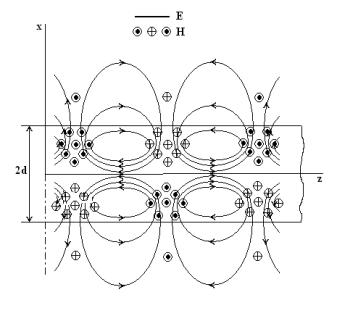
На рис.27 представлена рассчитанная структура поля волны H01.

Рис. 27 Структура поля волны H01

4.4 Расчет Н- образного диэлектрического резонатора

На базе волновода рассмотренного в параграфе 4.1 можно создать Н-

образный объемный диэлектрический резонатор.

Для этого необходимо данный волновод ограничить металлическими торцевыми стенками. Если расстояние между торцевыми стенками взять кратным половине длины волны в волноводе, то в резонаторе возникнет резонанс.

Задание:
Рассчитать Н-образный объемный диэлектрический резонатор для									волны
электрического	чѐтного типа	Е201 на частоте	f=10 ГГц.				Относительная
диэлектрическая	проницаемость	диэлектрика		r	=4,	r	1 ,	tg	10 4 .
				r		r

Окружающая среда - воздух. При расчете считать диэлектрическую пластину неограниченной по оси у.

В курсовую работу входит расчет следующих параметров резонатора:

поперечных волновых чисел, толщины слоя диэлектрика 2d, коэффициента распространения , длины волны волновода , определение его добротности.

Необходимо также записать уравнения, определяющие структуру поля в резонаторе, и на основании этих уравнений построить структуру поля волны Е201.

Расчѐт резонатора

1. В параграфе 4.1 проведѐн расчѐт волновода для заданных параметров и заданного типа волны Е20. Поэтому в данном примере мы можем воспользоваться результатами данного расчѐта (d=1см, в 2 ,57 см) и определить

его геометрические размеры: длину резонатора - она равна количеству полуволн,

укладывающихся при резонансе вдоль резонатора: h=l в =1,285 см и толщину

диэлектрика равную 2d=2 см .

2. Уравнения, определяющих структуру поля в резонаторе в случае волн

электрического чѐтного типа, имеют вид:

E zр

A sin( 1 x )cos

1 x sin

- диэлектрик (область I), (4.4.1)

E xp

A cos

j a

A cos 1 x cos

H yp

B e 2 x cos

B e 2 x sin

воздух ( область II) . (4.4.2)

E xp

j 0

H yp

B e

cos

3. Определение собственной добротности резонатора.

Q 0

Q 0 d

Q 0 м

Добротность Q 0 d

a E 2 dv

может быть определена при известном

д E

2 dv

tg .

Добротность,

обусловленная потерями в торцевых стенках, может быть

определена из интеграла:

Q 0 м

2 dv

2 м H 2 ds

Здесь в - длина волны в

волноводе,

-глубина

проникновения поля в

металл,

которая равна

1 /

0 м

Так как проводимость металла очень

высока,

например,

для

меди она равна

5 ,8 10 7

См/м,

то потери в резонаторе,

практически определяются только потерями в диэлектрике. Так при tg 10 3 ,

добротность резонатора

Q 0 1000 .

4. Структура поля строится на основании выражений (4.4.1), ( 4.4.2).

4.5 Расчет круглого планарного резонатора

Исходные данные:

Тип резонатора: Круглый планарный диэлектрический. Тип колебаний: E 1 1 0 , т.е.

m=1, n=1, l=0. Рабочая частота f0= 3,3 ГГц. Толщина диэлектрика: h =0,2 см.

Относительная диэлектрическая проницаемость: εr = 2,8. Волна Е110.

Расчет структуры поля резонатора

Так как данный тип

колебаний не имеет вариаций поля вдоль оси z (

=0) и

не имеет продольной составляющей магнитного

поля ( H z 0 ),

то

для

определения проекций

векторов поля на оси координат уравнения

(1.4а) и

(1.4б ) нужно записать в следующем виде:

j a 0 E

0 E

0 E z ,

j 0 0 H

0 H

0 H z .

E z

Откуда

Е Z

0 .

( 4.5.1)

Используя решение волнового уравнения

2 E Z

Е Z

2 E

2 2

виде Еz=(AJ m (

)+BN m (

))(Ccosm +Dsin )

исключая

из

решения

функцию

Неймана в соответствии

с требованием

теоремы

единственности,

										99
учетом граничных условий Олинера:						Е Z		0 при	= а , запишем выражение для
учетом граничных условий Олинера:								0 при	= а , запишем выражение для

Еz:
				Еz= Ez0 ∙ Jm(	mn		) ∙ cos(mα) .			(4.5.2)
				Еz= Ez0 ∙ Jm(			) ∙ cos(mα) .			(4.5.2)
					a
Здесь	mn	, а		- корень производной функции Бесселя первого рода m-го
Здесь		, а	mn	- корень производной функции Бесселя первого рода m-го
	a		mn
	a
порядка, a - радиус резонатора.
Используя выражение для Еz (4.5.2) и систему (4.5.1),										получим уравнения

для составляющих векторов поля колебаний типа Emn0. Для заданного поля (m=1,

n=1,

1 .84 )

решения

данных

уравнений,

определяющие

структуру поля

запишутся:

Ez = E z 0

J1(

1 .84

)cos(α),

= j H 0 J1 (

1 .84

)sin(α),

(4.5.3)

=- j H 0 J1

(

1 .84

)cos(α),

где

H 0

= E z 0

, H 0

E z 0

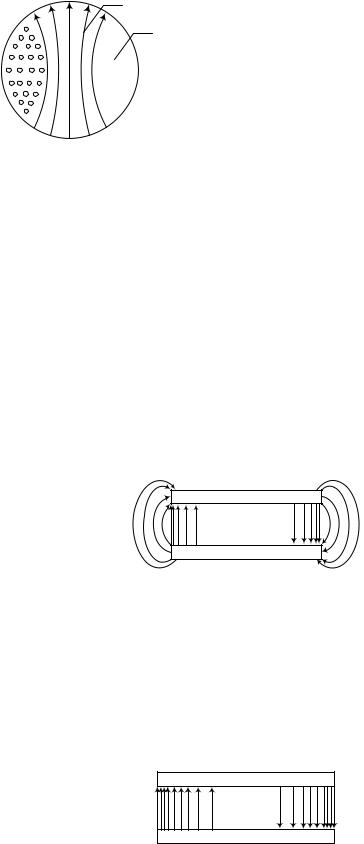
Структура поля типа Е110, построенная в соответствии с выражениями (4.53),

показана на рис.28.

100

+ + + + + + ++ + + ++ + + + + + + + + + +

Рис. 28 Структура поля типа Е110

Расчѐт геометрических размеров резонатора

В плоских резонаторах существует неоднородное заполнение. Между металлическими пластинами находится диэлектрик с относительной диэлектрической проницаемостью εr. Резонатор окружен воздухом.

Электрическое поле выходит за пределы диэлектрика и частично находится в воздухе (рис.29).

εr

Рис. 29 Геометрия резонатора Поэтому необходимо резонатор с неоднородным заполнением заменить

эквивалентным ему резонатором с однородным диэлектриком (рис.30),

проницаемость которого равна ε0 εr эф .

εr эф

Рис. 30 Геометрия эквивалентного резонатора Эквивалентный резонатор будет обладать «эффективными» размерами,

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 1210 11 12 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
05.02.20239.2 Mб16Распределенные сервис-ориентированные системы..pdf
#
05.02.2023283.13 Кб10Распространение лазерных пучков..pdf
#
05.02.20235.51 Mб97Распространение радиоволн и антенно-фидерные устройства..pdf
#
05.02.20231.52 Mб47Распространение радиоволн..pdf
#
05.02.2023425.46 Кб15Расчет деформационно-прочностных свойств композиционных материалов и напряженно-деформированного состояния простейших конструкций..pdf
#
05.02.20231.98 Mб33Расчет диэлектрических волноводов и объемных резонаторов..pdf
#
05.02.2023259.91 Кб14Расчет допусков и посадок сопрягаемых деталей..pdf
#
05.02.2023306.65 Кб20Расчет импульсной и переходной характеристик цепи..pdf
#
05.02.2023332.92 Кб34Расчёт надёжности функционального узла РЭС..pdf
#
05.02.20232.43 Mб12Расчет неуправляемого выпрямителя..pdf
#
05.02.2023131.15 Кб14Расчет переходных процессов классическим и операторным методами в цепях второго порядка..pdf