94

8 ДЕРЕВЬЯ И/ИЛИ

8.1 Основные понятия

Деревом И/ИЛИ является дерево, которое имеет два типа узлов (И­ узел и ИЛИ­узел). Впервые понятие И/ИЛИ дерева появилось в работе Слайгла [ ]. ИЛИ­узел означает, что задача может быть решена, если решать задачу 1, или задачу 2, или задачу 3 (рис. 8.1).

Рис. 8.1 — Узел ИЛИ

И­узел означает, что задачу можно разложить на подзадачи и, решив все задачи из этого списка, получить решение исходной задачи (рис. 8.2).

95

Рис. 8.2 — Узел И

Вариантом дерева И/ИЛИ назовем поддерево, которое получается из заданного путем отсечения выходных дуг кроме одной, у всех ИЛИ­узлов. Вариант в терминах решения задачи задает вариант решения задачи.

Деревья И/ИЛИ получили распространение в исследованиях по ис­ кусственному интеллекту [44–47]. Ниже предлагаются эффективные алго­ ритмы для перечисления вариантов в дереве И/ИЛИ [14].

8.2 Алгоритм подсчета вариантов

Рассмотрим алгоритм подсчета вариантов решений в дереве И/ИЛИ. Для этого запишем следующую рекурсивную функцию:

где z — рассматриваемый узел дерева; { siz } — множество сыновей узла z;

n — количество сыновей.

Подсчитав значение функции для корня дерева, можно получить об­ щее число вариантов подстановок, имеющихся в данном дереве. При этом

96

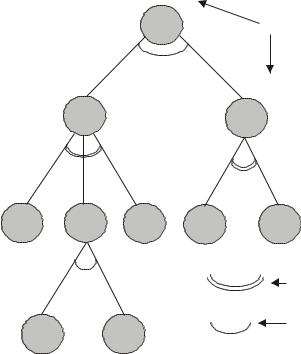
будет подсчитано количество вариантов подстановок для каждого узла всего дерева. Пример подсчета вариантов показан на рис. 8.3.

Рис. 8.3 — Пример подсчета вариантов в И/ИЛИ дереве

8.3 Алгоритм нумерации вариантов

Далее, используя значения функции для каждого узла, можно по­ строить алгоритм нумерации вариантов. Этот алгоритм по номеру из данно­ го дерева получает необходимый вариант подстановки. Предварительно за­ дадим две функции нумерации, которые по номеру варианта для рассмат­ риваемого узла вычисляют номера вариантов для сыновей. Для И­узла бу­ дет следующая функция:

где z — рассматриваемый узел дерева; { siz } — множество сыновей узла z;

(SiZ ) — количество вариантов в поддереве с узлом SiZ .

Примечание. При выполнении операции деления используются алго­ ритмы целочисленной арифметики.

Рассмотрим пример использования этой функции. Пусть задан

97

Для ИЛИ­узла необходимо определить не только номер варианта, но и номер соответствующего сына. Для этого запишем следующую функцию:

где z — рассматриваемый узел дерева; { siz } — множество сыновей узла z;

(SiZ ) — количество вариантов в поддереве с узлом SiZ . Рассмотрим пример. Пусть задан ИЛИ­узел с 3 сыновьями и (z) 9

Алгоритм определения варианта подстановки по заданному номеру будет следующий.

1.Первоначально производится подсчет количества вариантов для каждого узла дерева.

2.В вариант записывается корень дерева, и он становится текущим

узлом.

3.Определяется тип текущего узла. Если это И­узел, то переход на шаг 4, иначе переход на шаг 5.

4.Все сыновья рассматриваемого узла записываются в данный вари­ ант подстановки и для них соответственно с функцией для И­узлов опреде­ ляются номера вариантов для соответствующих поддеревьев (см. 2.11).