
Волновые процессы
..pdf
11
Естественным обобщением формулы (2.10) на случай плоской волны (в том числе и векторной), распространяющейся в произвольном направление, не совпадающем не с одной из координатных осей является формула
V = Aexp[i(wt - k × r )], |
(2.12) |
где A – векторная амплитуда волны, k × r = kx x + k y y + k z z – скалярное про-
изведение радиус вектора r = xxo + yyo + zzo на волновой вектор k = kx xo + k y yo + kz zo ; xo, yo и zo – орты координатной системы (см. рис. 2.3).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
φ=const3 |
|
|||
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
φ=const2 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
90o |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
zo |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
φ=const1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
r |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|||||||
|
|
|
|
|
|
|
|
|
yo |
|
|
|
|
|
|
|
|||
|
|
|
xo |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
x
Рис. 2.3. Произвольная ориентация плоскостей равных фаз в пространстве
Отметим, что уравнение kx x + k y y + kz z + wt = const есть уравнение семейства плоскостей перпендикулярных волновому вектору k.
2.3. Цилиндрические и сферические волны
Существуют другие типы волн, которые могут быть описаны выражением, аналогичными формуле (2.10)
V = Af (r )exp[if(wt - k × r )], |
(2.13) |
12
где f (r ) и f(wt - k × r ) – скалярные вещественные функции с векторным ар-
гументом.
При такой записи поверхность равных фаз, которую также называют волновым фронтом [***], определяется уравнением f(wt - k × r ) = const .
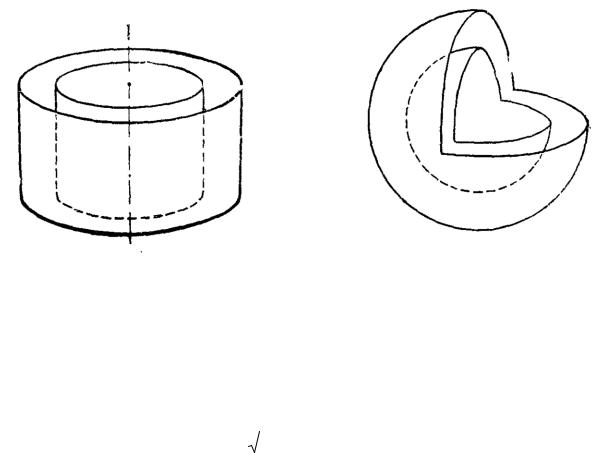
Широко известными являются цилиндрические и сферические волновые фронты.
Рис. 2.4. Волновые фронты цилиндрической и сферической волн
Цилиндрические волны, для случая kρ>>1, где ρ – расстояние от оси волнового фронта, описываются соотношением [***]
V = A |
1 |
|
exp[i(ωt − kρ)]. |
(2.14) |
|
|
|
|
|||
|
ρ |
||||
|
|
|
|
|
|
В этом случае уравнение f(wt - k × r ) = wt - kr = const есть уравнение цилин-
дра. Отметим, что поверхность равных амплитуд также является цилиндром, т.е. совпадает с поверхностью равных фаз.
Сферические волны, для случая kr>>1, где r – расстояние от центра волнового фронта, описываются соотношением [***]
V = A |
1 |
exp[i(ωt − kr )]. |
(2.15) |
|
r
13
В этом случае уравнение f(wt - k × r ) = wt - kr = const есть уравнение сферы.
Отметим, что поверхность равных амплитуд также является сферой, т.е. совпадает с поверхностью равных фаз.
Круг волновых явлений далеко не ограничивается перечисленными выше волновыми процессами. Их многообразие настолько велико, что задача их перечисления скорее всего не будет решена точно. Помимо некоторых простых свойств волновых процессов, рассмотренных выше, они обладают и более сложными свойствами, связанными с физической природой волны, с влиянием среды распространения, со взаимодействием волновых полей одной и той же физической величины между собой, со взаимодействием волновых полей различной физической природы и другими факторами. Данное выше интуитивное математическое описание волновых процессов является простым введением, необходимым для понимания того, каким основным условиям должны удовлетворять решения строгих математических моделей физических полей должны быть найдены при описании волн этих полей.
3. Электромагнитные волны
3.1. Уравнения Максвелла, материальные уравнения и граничные условия Из общего курса физики известно, что электромагнитное поле в произвольной среде описывается уравнениями Максвелла (см., например,
[****]), которые в дифференциальной форме могут представлены в виде:
Ñ × D = r; |
(3.1) |
Ñ × B = 0 ; |
(3.2) |
Ñ ´ E = - ∂B ; |
(3.3) |
¶t |
|
Ñ ´ H = J , |
(3.4) |
14
где D и B – векторы электрической и магнитной индукции; E и H – векторы
электрической и магнитной напряженности; |
r – |
объемная плотность элек- |
||||||
трического заряда; J – вектор плотности электрического тока. |
||||||||
При записи уравнений (3.1)–(3.4) |
использовался символический |
|||||||
векторный дифференциальный оператор |
|
|
|
|||||
Ñ = xo |
∂ |
+ yo |
|
∂ |
+ zo |
∂ |
. |
(3.5) |
|
|
|
||||||
|
¶x |
|
¶y |
¶z |
|
|||
Запись Ñ ×V есть оператор дивергенции над вектором V, записан- |
||||||||
ный в символьном виде. Так как |
V в координатной форме имеет вид |
|||||||
V =Vx xo + Vy yo + Vz zo , то, используя свойство |
скалярного произведения |
|||||||
двух векторов, доказанное в курсе линейной алгебры и аналитической геометрии [***], можно получить следующее соотношение
Ñ ×V = |
¶V |
x + |
∂Vy |
+ |
¶V |
z . |
(3.6) |
|
¶y |
|
|||||
|
¶x |
|
¶z |
|
|||
Запись Ñ ´V есть оператор ротора над |
вектором V. Используя |
||||||
свойство векторного произведения двух векторов можно получить следующее соотношение
|
|
xo |
|
yo |
|
z o |
|
|
|
¶V |
|
|
¶Vy |
|
|
|
¶V |
|
|
¶V |
|
|
¶Vy |
|
¶V |
|
|
|
||
|
¶ |
¶ |
¶ |
|
|
z |
|
|
o |
|
x |
|
z |
|
|
x |
|
|||||||||||||
Ñ ´V = |
|
|
|
|
|
|
|
= x |
o |
|
- |
|
|
+ y |
|
|
- |
|
+ z |
o |
|
- |
|
|
.(3.7) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
¶x |
|
¶y ¶z |
|
|
¶y |
¶z |
|
|
¶z |
¶x |
|
¶x |
¶y |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
Vx |
Vy |
Vz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Система (3.1)–(3.4) незамкнута. Однозначно замыкают систему ее материальные уравнения, связывающие между собой физические величины
D, B, E, H, r, J, как функции времени t и радиус-вектора r. Ограничения, налагаемые материальными уравнениями и соответствующими им физическими процессами в различных средах, определяют характер протекающего электромагнитного процесса. Для большого количества различных извест-
15
ных материальных сред связь векторов электромагнитного поля D и E может быть представлена в виде
D = e0ε × E
где
|
exy |
exx |
|
ε = exy |
e yy |
|
e yz |
exz |
(3.8)
e
xz
e yz (3.9)
ezz
тензор (второго ранга валентности три [***]) относительной диэлектриче-
ской проницаемости, e0 – фундаментальная электрическая постоянная [***]. Последнее соотношение может быть записано в следующем развернутом виде
D |
|
|
e |
xx |
|
x |
|
|
|
Dy |
= e0 |
exy |
||
|
|
|
|
|
Dz |
|
exz |
||
или в виде
e |
xy |
e |
|
E |
|
|
e |
xx |
E |
x |
|
|
xz |
|
x |
|
|
|
|||
e yy |
e yz |
× E y |
= e0 |
exy Ex |
||||||
e yz |
|
|
|
|
|
|
|
|
|
|
ezz |
Ez |
|
exz Ex |
|||||||
+exy E y
+e yy E y
+e yz E y
|
|
+ exz Ez |
|
+ e yz Ez , |
(3.10) |
|
|
+ ezz Ez |
|
+ e0 (exy Ex + e yy E y + e yz Ez )yo + e0 |
|
|
(3.11) |
||||||
(exz Ex + e yz E y + ezz E )zo |
|||||||||
Dx xo + Dy yo |
+ |
Dz zo = e0 |
(exx Ex |
+ exy E y + exz Ez )xo + |
|
||||
Аналогичная связь существует и между векторами B и H |
|
||||||||
B |
|
m |
xx |
m |
xy |
m |
xz |
|
|
|
x |
|
|
|
|
|
|||
B = By |
= m0 mxy |
m yy |
m yz |
× H = m0μ × H . |
(3.12) |
||||
|
|
|
|
m yz |
|
|
|
|
|
Bz |
mxz |
mzz |
|
||||||
μ – тензор относительной магнитной проницаемости, m0 – |
фундаментальная |
||||||||
магнитная постоянная. |
|
|
|
|
|
|
|
|
|
16
Мы будем рассматривать случаи, когда вклад в вектор плотности электрического тока дают только ток смещения и ток проводимости и заданный сторонний ток
J = |
∂D + σ × E + Jст, |
(3.13) |
|
¶t |
|
где σ – тензор проводимости на частоте светового поля w. Кроме того во всех вопросах, рассмотренных в этом разделе, плотность электрического заряда будет заданной функцией времени и координат (чаще всего она будет равна нулю). При этих условиях система уравнений (3.1)-(3.4), (3.8), (3.12) и (3.13) является замкнутой.
Отметим, что уравнения Максвелла могут быть записаны в эквивалентной интегральной форме [***], которая удобна при выводе граничных условий, связывающих электромагнитные поля на границе раздела двух сред. Здесь мы не будем использовать интегральную форму уравнений, а сразу приведем граничные условия, методика получения которых хорошо представлена в учебной литературе (см., например, [***]):
EτI |
- EτII = 0 , |
(3.14) |
D I |
- D II = x , |
(3.15) |
n |
n |
|
BnI |
- BnII = 0 , |
(3.16) |
H τI |
- H τII = h, |
(3.17) |
где нижний индекс «t» относится к составляющим полей, тангенциальным (касательным) к границе раздела сред I и II (верхний индекс); нижний индекс «n» относится к составляющим полей, нормальным (перпендикулярным) к
границе раздела сред I и II; x поверхностная плотность электрического заряда
17
на границе раздела сред; h поверхностная плотность электрического тока на границе раздела сред.
3.2.Волновое уравнение в однородной анизотропной среде без токов и зарядов
Вэтом случае диэлектрическая и магнитная проницаемость и проводимость среды описываются скалярными величинами. Кроме того выполняют-
ся равенства r=0 и Jст=0. Применяя операцию Ñ ´ к уравнениям (3.3), (3.4) и учитывая уравнения (3.8), (3.12) и (3.13)
Ñ ´ Ñ ´ E = -m0m |
∂ |
Ñ ´ H ; |
|
(3.18) |
|||||
|
|
||||||||
|
|
|
|
¶t |
|
|
|
||
Ñ ´ Ñ ´ H = e0e |
∂ |
Ñ ´ E + sÑ ´ E , |
(3.19) |
||||||
|
|||||||||
|
¶t |
|
|
|
|
|
|||
Учитывая выражение |
|
|
|
|
|
|
|
||
Ñ ´ H = e0e ∂E + sE , |
|
|
(3.20) |
||||||
|
|
|
¶t |
|
|
|
|
|
|
уравнение (3.18) может быть преобразовано к виду |
|
|
|||||||
Ñ ´ Ñ ´ E + m0e0me |
¶2 E |
+ m0ms |
¶E |
= 0 . |
(3.21) |
||||
¶t 2 |
¶t |
||||||||
|
|
|
|
|
|
||||
Последнее уравнение удобно тем, что в него входит одна неизвестная вектор функция – напряженность электрического поля. Это уравнение может быть упрощено при помощи известной формулы векторного анализа
Ñ ´ Ñ ´ E = Ñ(Ñ × E ) - Ñ2 E = Ñ(Ñ × E ) - DE , |
(3.22) |
где
|
|
|
|
|
|
18 |
|
Ñ2 = D = |
¶2 |
+ |
¶2 |
+ |
¶2 |
(3.23) |
|
¶x2 |
¶y 2 |
¶z 2 |
|||||
|
|
|
|
скалярный дифференциальный оператор Лапласа. Из уравнения (3.1), усло-
вия r=0 и того, что среда изотропная следует, что Ñ × E = 0 |
и Ñ(Ñ × E ) = 0 . |
|||||
Тогда уравнение (3.21) может быть преобразовано к виду |
|
|||||
DE - m0e0me |
¶2 E |
- m0ms |
¶E |
= 0 . |
(3.24) |
|
¶t 2 |
¶t |
|||||
|
|
|
|
|||
Последнее уравнение носит название волнового уравнения для поглощающей среды.
Учитывая выражение
Ñ ´ E = -m0m |
∂H , |
(3.25) |
|
¶t |
|
уравнение (3.19) также может быть преобразовано к форме
Ñ ´ Ñ ´ H + e0m0em |
¶2 H |
+ m0ms |
¶H |
= 0 , |
(3.26) |
||
¶t |
2 |
¶t |
|||||
|
|
|
|
||||
Последнее уравнение по своей форме аналогично форме уравнения (3.21). Оно также может быть сведено к форме волнового уравнения
DH - m0e0me |
¶2 H |
- m0ms |
¶H |
= 0 . |
(3.27) |
||
¶t |
2 |
¶t |
|||||
|
|
|
|
||||
3.3. Общее решение волнового уравнения в непроводящей среде Покажем, что любая функция вида E(wt m k × r ) является решением
волнового уравнения (3.24) при s=0. Введем новую переменную
x = wt m k × r .
Тогда
19
DE(wt m k × r ) = |
¶2 E(wt m k × r ) |
+ |
¶2 E(wt m k × r ) |
+ |
¶2 E(wt m k × r ) . |
|
¶x2 |
|
¶y 2 |
|
¶z 2 |
Рассмотрим для примера одну из вторых производных в последнем соотношении
¶2 E(wt m k × r ) |
|
|
¶ ¶E(wt m k × r ) |
|
¶ |
¶E(x) ¶x |
|
|
|||||||||||||
¶x2 |
|
|
= |
|
|
|
¶x |
|
|
= |
|
|
|
|
|
|
= |
||||
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
¶x |
|
|
|
|
¶x |
|
¶x x |
. |
|||||||||
|
¶ |
|
|
¶E(x) |
|
|
¶ |
¶E(x) |
¶x |
|
|
2 ¶2 E(x) |
|
||||||||
|
|
|
|
|
|
|
|
||||||||||||||
= mkx |
|
|
|
|
|
|
= mkx |
|
|
|
|
|
|
= kx |
|
|
|
|
|||
¶x |
¶x |
|
|
|
¶x |
x |
¶x2 |
|
|
||||||||||||
|
|
|
|
|
|
¶x |
|
|
|
|
|
|
|||||||||
Тогда
DE(wt m k × r ) = (k x2 + k y2 + k z2 )¶2 E(x) |
= k |
2 ¶2 E(x) . |
¶x2 |
|
¶x2 |
В свою очередь
¶2 E(wt m k × r ) |
= w |
2 |
¶2 E(x) |
¶t 2 |
|
. |
|
|
|
¶x2 |
Поэтому
DE - m0e0me |
¶2 E = 0 Û |
(k |
2 - m0e0mew2 )¶2 E = 0 . |
(3.28) |
|
¶t 2 |
|
¶x2 |
|
Очевидно, что равенство выполняется, если
|
|
|
|
|
|
|
|
|
|
|
|
k 2 = m0e0mew2 Û k = |
|
|
mew |
= w |
= nk0 , |
|
|||||
m0e0 |
mew = |
(3.29) |
|||||||||
|
|
|
|||||||||
|
|
|
|
|
|
c |
|
u |
|
|
|
где c электромагнитных волн в вакууме; u = c

 me – их скорость в среде с относительной диэлектрической проницаемостью e и относительной магнит-
me – их скорость в среде с относительной диэлектрической проницаемостью e и относительной магнит-
20
ной проницаемостью μ; k0 – волновое число в вакууме; n = 
 με – показатель преломления среды.
με – показатель преломления среды.
Формула (3.29) совпадает с формулой (2.9), полученной на основе простых представлений о волновом процессе.
Напомним, что длина волны λ в случае вещественного значения волнового числа k определяется соотношением l = 2p k . Она равна рас-
k . Она равна рас-
стоянию между двумя ближайшими точками волнового процесса, в кото-
рых фаза волны отличается на 2π.
Таким образом, если частота и скалярный квадрат волнового вектора связаны соотношением (3.29), то любая функция вида E(wt m k × r ), опи-
сывающая вектор электрической напряженности, является решением волнового уравнения (3.24) для свободного непроводящего пространства. Очевидно, что функция H (wt m k × r ), описывающей вектор магнитной напряженно-
сти, является решением волнового уравнения (3.27). Указанные функции описывают волны, недеформирующиеся при распространении.
3.4.Плоские электромагнитные волны в однородной изотропной среде, свободной от токов и зарядов
Очевидно, что плоская волна вида (2.12) будет решением волнового уравнения волнового уравнения (3.24) или (3.27) при σ=0. Следует отметить, что при записи плоской волны в форме (2.12) конкретизируется только фор-
ма волнового фронта, а параметры волны, такие как частота ω и волновой вектор k остаются неизвестными. Они связаны с физическими параметрами среды распространения и могут быть определены при анализе математической модели волнового процесса. Примером такого определения является соотношение (3.29), позволяющее вычислить величину волнового вектора и частоту через показатель преломления среды и волновое число в вакууме.
На практике обычно частота известна и требуется определить величину волнового вектора. В рассматриваемом случае направление волнового вектора в пространстве также считается заданным. Часто оно задается еди-
