
Компьютерная геометрия и графика
..pdf
|
|
81 |
|
Пусть одна кривая Безье определена точками P0 Pn , |
а другая точками |
||
Q0 ÷Qm . Непрерывность первого порядка имеет место, если |
|
||
′ |
′ |
скаляр |
|
P (1) = gQ (0), где g – |
|
||
Имеем |
|
|
|
n(Pn − Pn−1) = gm(g −Q0 ) |
|
||
Раз кривые сопрягаются, то Pn = Q0 |
|
||
Таким |
образом, для |
обеспечения непрерывности |
первого порядка |
требуется, чтобы конечный отрезок первого многоугольника и начальный отрезок второго лежали на одной прямой (или точки Pn−1, Pn = Q0 ,Q0 – на одной прямой).
|
|
Q3 |
P1 |
P2 |
|
|
P3 |
|
|
Q0 |
Q2 |
P0 |
|
Q1 |
|
|
Рисунок 4.4
4.4В-СПЛАЙНЫ
Еще одним методом построения гладкой кривой между двумя точками (концами), форма отдельных участков которой определяется промежуточными точками, является метод В-сплайнов.
Вначале определим понятие В-сплайна. Произвольная точка кривой P(t) ,
то есть ее вектор положения, задается в В-сплайн базисе следующим образом:
n
P(t) = ∑Pi Νi,k (t) ,
i=0
Здесь Pi – вершины характеристического многоугольника, i = 0,1;
Νi,k – базисные функции; k – порядок кривой;
82
t – параметр, изменяющийся в диапазоне от 0 до tmax .
В отличие от метода кривых Безье, где 0 < t <1, в методе В-сплайнов величина tmax ≠ 1 и определяется порядком кривой, а также наличием так называемых кратных вершин, которые мы рассмотрим чуть ниже.
Для определения базисных функций Νi,1 введем понятие узлового вектора.
Узловой вектор или вектор параметрических узлов представляет собой последовательность целых положительных чисел qj
|
,q 2 ,..,qj+1 |
|
, |
|
|
|
|
q1 |
|
|
|
|
|
||
в |
которой |
|
qj |
< t < qj+1 . |
Примерами |
узлового |
вектора является |
[0 1 2 |
3 4] |
или |
[0 0 0 |
1 1 2 3 |
3 3] и |
т.д. Значения qj |
|
рассматриваются как параметрические узлы, характеризующие различные интервалы изменения параметра t . Размерность узлового вектора и конкретные значения узлов зависят от числа вершин задающего многоугольника, то есть от n , порядка кривой k и сложности вершин.
Сложная (или кратная) вершина это две или более вершины с одинаковыми координатами. В узловом векторе сложным вершинам соответствует последовательность одинаковых по величине компонентq1,qi+1,..,qi+l−1 , где l – кратность вершины.
Алгоритм формирования узлового вектора следующий. Входными параметрами являются:
–массив вершин задающего многоугольника, в котором l – кратная вершина
представлена как l – простых вершин с совпадающими координатами – массив
P[n +1] ;
–n – число вершин без l;
–k – порядок кривой.
На выходе формируется вектор q .
83
Размерность вектора q определяется, как n + 2(k −1), то есть
q=[qn ,qn+1,..,qn+K ] ;
1)Для 0 < j < k −1 qj = 0 ;
2) Для k < j < n +1, если Pj−K ≠ Pj−K +1 , то qj = qj−1 +1; если Pj−K = Pj−K +1 , то
qj = qj−1 ; |
|
|
|
|
|
|
|
|
|
3) Для n + 2 < j < n + k |
qj = qj−1. . |
|
|
|
|
|
|||
Например, если задающий многоугольник содержит пять вершин, то есть |
|||||||||
n = 4, порядок |
кривой |
k = 2 |
и |
отсутствуют |
сложные |
вершины, |
то |
||
q =[0 0 1 2 3 4 4]; |
|
|
|
|
|
|
|
|
|
если k = 3, то q =[0 |
0 |
0 |
1 2 |
3 3 3] ; |
|
|
|
|
|
если одна из вершин, |
например P1 , двойная, |
то есть |
массив |
вершин |
|||||
включает P0 , P1, P1, P2 , P3, P4 , |
или |
P0 , P1, P2 , P3, P4 , P5 , где |
P1 = P2 , |
то есть |
n = 5 |
и |
|||
k = 2 , то |
|
|
|
|
|
|
|
|
|
q =[0 0 1 1 2 2 3 3 4 4] ; |
|
|
|
|
|||||
если n = 3, то q =[0 |
0 0 1 1 2 3 3 3] . |
|
|
|
|
||||
Отметим одно общее правило: начальные и конечные вершины условно |
|||||||||
считываются k |
– кратными, |
однако, |
в отличии от кратных промежуточных |
||||||
вершин, это не приводит к увеличению n , а лишь отражается в узловом векторе.
Теперь определим базисные функции Νik (t) .
Они задаются рекуррентным соотношением
|
|
1, |
åñëè qi |
< t < qi+1 |
; |
|
|||
Νi,1(t) = |
â |
п ро т ивн о м случае |
|
||||||
|
0 |
|
|
||||||
Νi,K |
(t) = |
t − qi |
|
Νi,K −1 |
(t) + |
qi+K −t |
Νi+1,K −1(t) . |
||
|
|
|
|||||||
|
|
qi+K −1 − qi |
|
qi−K − qi+1 |
|||||
Отсюда видно, что если порядок кривой равен k , то функция Νi,K (t) ,
соответствующая I – вершинеP1 , не равна нулю только на промежутке
84
q1 < t < q1+K то есть каждая вершина P1 имеет ограниченное (локальное)
влияние на форму кривой.
Метод В-сплайнов позволяет изменить форму кривых и добиваться нужной формы различными способами – изменяя количеством положение вершин, их сложность, порядок кривой и так далее. Если порядок кривой k равен числу вершин и отсутствуют сложные вершины, то В-сплайн кривая совпадает с кривой Безье; с уменьшением порядка форма кривой приближается к форме описывающего ее многоугольника.
При k = 2 кривая полностью совпадает с многоугольником. Рассмотрим пример.
Пусть многоугольник состоит из четырех вершин: P0 , P1, P2 , P3, то есть n = 3 . Пусть k = 2 .
Тогда q =[ |
0 0 1 |
|
2 |
3 |
3] , т.е q0 = 0, q1 = 0, q2 =1, q3 = 2, q4 = 3, q5 = 3; |
||||||||||||||||||||||
Определим функцию Ν . При этом будем считать, что 0/0 = 0 |
|||||||||||||||||||||||||||
Ν |
0,2 |
(t) = |
|
t − q0 |
|
|
Ν |
0,1 |
(t) + |
|
|
q2 −t |
Ν |
1,1 |
(t) ; |
||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
q1 |
− q0 |
|
|
q2 − q1 |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Ν |
1,2 |
(t) = |
|
|
t − q1 |
|
Ν |
|
(t) + |
|
|
q3 −t |
Ν |
2,1 |
(t); |
||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
q2 |
− q1 |
|
|
|
q3 − q2 |
|
|
|
|
|
||||||||||||||
Ν |
2,2 |
(t) = |
t − q2 |
Ν |
2,1 |
(t) + |
|
|
q4 −t |
|
Ν |
3,1 |
(t) ; |
||||||||||||||
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
q3 |
− q2 |
|
|
|
q4 − q3 |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Ν |
3,2 |
(t) = |
t − q3 |
Ν |
3,1 |
(t) + |
|
|
qS −t |
Ν |
4,1 |
(t) . |
|||||||||||||||
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
q4 |
− q3 |
|
|
qS |
− q4 |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Заполним таблицу:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
85 |
|
t |
|
N0,2 |
N1,2 |
|
|
N2,2 |
N3,2 |
P(t) |
|||||||||||||
0 |
1 |
|
|
0 |
0 |
|
|
0 |
P0 |
|
|||||||||||
0.5 |
0.5 |
|
|
0.5 |
0 |
|
|
0 |
0.5(P0 + P1) |
||||||||||||
1 |
0 |
|
|
1 |
0 |
|
|
0 |
P1 |
+ P ) ; |
|||||||||||
1.5 |
0 |
|
|
0.5 |
0.5 |
|
|
0 |
0.5(P |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
2 |
0 |
|
|
0 |
1 |
|
|
0 |
P2 |
||||||||||||
2.5 |
0 |
|
|
0 |
0.5 |
|
|
0.5 |
0.5(P2 + P3 ) |
||||||||||||
3 |
0 |
|
|
0 |
0 |
|
|
1 |
P3 |
||||||||||||
t = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ν = |
0 −0 |
+ |
|
1−0 |
1 =1 |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
||||||||||||||
|
0,2 |
|
|
0 −0 |
|
|
|
1−0 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 −0 |
|
|
|
|
|
2 −0 |
|
|
|
; |
|
|
||||||
Ν = |
+ |
|
0 = 0 |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||
|
1,2 |
|
1−0 |
2 |
−1 |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ν2,2 = Ν3,2 = 0 |
|
|
|
|
|
|
|
|
|
|
|||||||||||
t = 0.5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Ν |
|
= |
0.5 −0 |
0 + |
1−0.5 |
1 = 0.5 |
|
|
|||||||||||||
0,2 |
|
|
|
|
|
|
|||||||||||||||
|
|
|
0 −0 |
|
|
1−0 |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ν |
|
= |
0.5 −0 |
1+ |
2 −0.5 |
0 = 0.5 |
|
|
|||||||||||||
1,2 |
|
|
|
|
|||||||||||||||||
|
|
|
1−0 |
|
|
|
|
|
|
|
2 −1 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ν2,2 = Ν3,2 = 0
итак далее.
Далее, |
P(t) = P0Ν0,2 (t) + P1Ν1,2 (t) + P2Ν2,2. (t) + P3Ν3,2 (t) . |
При |
t = 0, P(0) = P01+ P10 + P2 0 + P3 0 = P0 |
t = 0.5 , |
P(0.5) = P0 0.5 + P10.5 = (P0 + P1) |
t =1, |
P(1) = P1 . |
Таким образом, мы убедились, что при k = 2 кривая совпадает с задающим многоугольником.
Проиллюстрируем теперь различные способы коррекции формы В- сплайн кривой.
Изменение порядка кривой.
при k = 2 кривая совпадает с многоугольником;
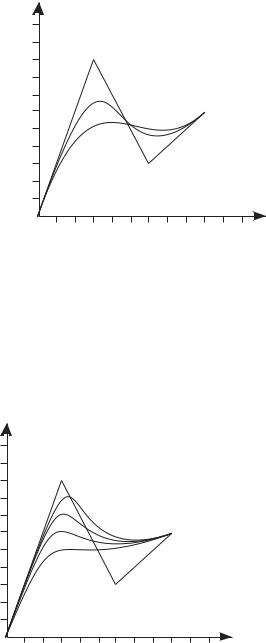
86
при k = 4 – это кривая Безье;
при k = 3 – промежуточное положение.
Чем выше порядок, тем больше форма кривой отличается от формы задающего многоугольника.
Y |
|
|
|
|
0 |
0 |
|
9 |
P |
|
|
|
3 |
9 |
|
1 |
|
|
|
|
|
|
|
|
|
|
P= |
|
|
|
|
|
k=2 |
|
|
6 |
9 |
||
|
k=3 |
|
|
|
|
||
6 |
|
P3 |
|
9 |
6 |
|
|
k=4 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
P2 |
|
|
|
|
|
P0 |
3 |
6 |
9 |
X |
|
|
|
|
|
|
|
Рисунок 4.7 Увеличение сложности вершины с одновременным увеличением порядка.
(количество вершин / порядок)
4/4 – нет сложных вершин – кривая Безье; 5/5 – P1 – двойная вершина, то есть
Y |
|
|
|
|
|
|
|
|
P1 |
|
|
|
0 |
0 |
|
9 |
|
|
|
3 |
9 |
|
|
|
|
|
|||||
|
7/7 |
|
|
|
|
||
|
6/6 |
|
|
P = |
3 |
9 |
|
6 |
5/5 |
|
P3 |
|
6 |
3 |
, k = 5; |
|
4/4 |
|
|
|
|
||
|
|
|
|
9 |
6 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
||
3 |
|
|
|
|
|
|
|
|
|
P2 |
|
|
|
|
|
P0 |
3 |
6 |
9 |
X |
|
|
|
|
|
|
|
||||
|
|
|
Рисунок 4.8 |
|
|
|
|
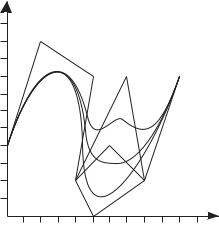
87
и так далее. То есть сложные вершины подтягивают кривую к себе. Отметим, что в этом случае начальные и конечные наклоны кривой остаются неизменными.
Локальная коррекция формы – изменение положения одной вершины.
Y |
|
|
|
0 |
2 |
0 |
0 |
0 |
0 |
||
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
5 |
0 |
0 |
0 |
0 |
||
|
|
|
|
|
5 |
4 |
0 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P = |
4 |
1 |
0 |
0 |
0 |
0 |
|
3 |
|
|
|
|
5 |
0 |
6 |
2 |
7 |
4 |
, n = 6, k = 5 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
8 |
1 |
0 |
0 |
0 |
0 |
||
|
|
|
|
|
|
4 |
0 |
0 |
0 |
|
|
1 |
|
|
|
10 |
0 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
P0 |
3 |
6 |
9 |
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Рисунок 4.9
Видно, что изменение положения пятой вершины P4 не меняет начальную форму кривой. В этом проявляется локальная природа базисных функций Ν(t).
88
5 ОПИСАНИЕ И ПОСТРОЕНИЕ ПОВЕРХНОСТИ
Задача построения поверхностей возникает в таких областях, как проектирование самолетов, кораблей и так далее, при работе с местностью (ее участками) и так далее.
Традиционным способом описания поверхностей у конструкторов является ортогональные проекции, у картографов – линии равного уровня. Однако многие сложные поверхности не могут быть эффективно представлены таким образом. Для машинной графики актуальной является задача поиска эффективных описаний поверхности, с помощью которых ее затем можно отобразить (используя проекции) произвольным образом. Причем в простых случаях ищут единое математическое описание для всей поверхности, в более сложных – используют кусочную аппроксимацию (приближение) отдельных ее частей.
Рассмотрим различные методы аналитического (точного) и численного (приближенного) представления трехмерных поверхностей. Вначале отметим, что поверхность (или ее участок) может быть описана явно, неявно и параметрически:
–явно: z = f (x, y) ;
–неявно:
x = f (u, w)
– параметрически: y = g(u,w) .
z = h(u,w)
89
5.1СФЕРИЧЕСКИЕ ПОВЕРХНОСТИ
Неявное описание единичной сферы выглядит следующим образом:
x2 + y2 + z2 =1.
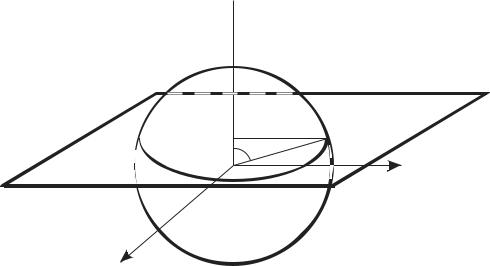
Характерные кривые на сферической поверхности могут быть получены с помощью плоскостей, которые ее пересекают. Пересечение единичной сферы и плоскости
z = cosΦ1 = a1
(плоскость, параллельная плоскости XOY и проходящая через точку z = a1 )
дает
x2 + y2 + a12 =1, то есть
x2 + y2 =1− a12 .
Мы получили уравнение окружности, которая называется широтой.
Широта
Z 
a1 Φ1
z = cos Φ1
r=1
Y
X
90
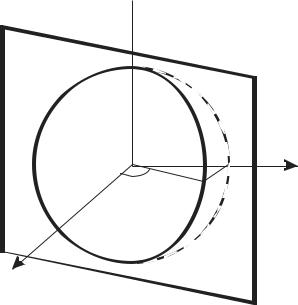
Долгота
Z 
x s |
- |
|
|
|
in Θ |
y |
|
|
|
0 |
|
|
|
|
|
|
c |
|
|
|
|
os Θ |
= |
|
|
|
0 |
0 |
|
|
|
|
b1
Θ0 c1 Y
X
Рисунок 5.1
Пересечение сферы с плоскостью xsin Θ0 − y cosΘ0 = 0 или
c1x −b1 y = 0
дает окружность, называемую долготой:
|
2 |
|
|
|
|
y2 |
|
b1 |
+1 |
+ z2 |
=1. |
2 |
|||||
|
c1 |
|
|
|
|
Часто широтой и долготой называют не окружности, а углы Φ1 иΘ0 .
Участок сферической поверхности может быть образован четырьмя границами – это две широты и две долготы.
Параметрическое представление единичной сферической поверхности имеет вид:
x = cosΘ sin Φ
y = sin Θ cosΦ .
z = cosΦ
