Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Томский Государственный Университет Систем Управления и Радиоэлектроники

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Компьютерная геометрия и графика

..pdf

Скачиваний:

Добавлен:

05.02.2023

Размер:

634.52 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 78 / 118 9 10 11 > Следующая >>>

Рассмотрим сначала задачу проведения гладкой кривой через ряд заданных точек. Для её решения часто используют сплайновые сегменты.

4.2КУБИЧЕСКИЕ СПЛАЙНЫ

Физически сплайны можно представить в виде узкой деревянной рейки, лежащей концами на точках опоры, кривизны которой реализуется с помощью свинцовых грузов.

Рисунок 4.1

Математически сплайн описывается полиномом k – той степени. Чаще всего используют полиномы третьей степени – кубические сплайны. Конкретный вид кубического сплайна определяется координатами точек, через которые его надо провести (концевых точек) и наклоном в этих точках.

Если требуется провести гладкую кривую между n точками, то используется совокупность n −1 сплайнов – так называемые сплайновые сегменты. При этом предъявляется требование непрерывности второго порядка в местах соединений.

Уравнение единственного кубического сплайнового сегмента в параметрической форме выглядит следующим образом:

P(t) = B1 + B2t + B3t2 + B4t3 = ∑Biti−1,t1 < t < t2 ,

i=1

где P(t) =[x(t), y(t), z(t)] – вектор положения произвольной точки на сплайне.

Рисунок 4.2

Коэффициенты Bi ,i =1,4 определяются координатами концов сегмента P1

и P2 и				касательными векторами на концах P1′		иP2′, которые	являются
произвольными по параметру t .
Внутри					сплайнового сегмента параметр t	меняется от	t1 до t2
(t1 соответствуетP1,t2 − P2 ).
Обычно полагают t1 = 0 . Тогда
	P(0) = P1 ,
	P(t			) = P
		2			2
	dP				= P1′,
	dP
			t = 0
	dt
	dt
	dP				= P2′.
	dP
			t = t2
	dt
	dt

Отсюда получим:

P(0) = B1 = P1′,

dP		= B	+ 2B t +3B t2		t=0	=B = P′,
dP

dt	t = 0	2	3	4		2 1
dt	t = 0

P(t2 ) = B1 + B2t2 + B3t22 + B4t23 = P2 ,

= B

+ 2B t

+3B t2

= P′.

t = t2

3 2

Окончательно имеем:

B1 = P1 ,

= P1′,

3(P2 − P1)

−

2P1′−

P2′

B =

2(P1 − P2 )

−

P1′−

P2′

Отсюда уравнение одного кубического сплайнового сегмента:

3(P

− P )

2P'

2(P

− P )

P(t) = P + P't +

(

−

)t2 + (

−

)t3 .

Обобщение этого уравнения для любых двух смежных сегментов Pk (t)

Pk +1(t) , где 1< k < n − 2 имеет вид

3(P

− P

)

2P′

P (t) = P + P′t +

(

K =1

−

K +1

)t2 +

tK2 +1

tK +1

2(PK − PK +1)

PK′

−

PK' +1

)t3;

t22K =1

tK3 +1

tK2 +1

3(P

− P

)

2P′

(t)

= P

+ P′

t + (

K +1

−

+1K

−

K +2

)t2 +

tK2 +2

K +1

tK +2

2(PK +1 − PK +2 )

PK′+1

−

PK' +2

)t3.

tK3 +2

t22K =2

tK2 +2

При этом важно, что в уравнении

PK (t)

tk < t < tK +1

PK +1(t)

tk+1 < t < tK +2 .

Кривая в этом случае определяется тремя точками PK (t), PK =1(t), PK +2 (t)

касательными на концах, то есть

PK′

иPK′+2 . Касательная в точках PK +1 – PK′+1

определяется из условия непрерывности второго порядка – постоянства кривизны в точке соединенияPK +1 .

Вторая производная P(t)

P′′(t) = 2B3 + 6B4t при t = tK +1 в конце первого сегмента.

P′′(t) = 2B3 + 6B4tK +1

а в начале второго (t = 0) .

P′′ = 2B3 (это коэффициенты двух разных сплайновых сегментов).

Приравняем P в этих точках, подставим B3 и B4 :

2(PK − PK +1)

PK′

PK′=1

3(PK +1 − PK )

−

2PK′

−

PK′

6tK +1

tK +1

tK =1

3(PK +2 − PK =1)

−

2PK′

−

PK′

tK +2

tK =2

После преобразований (умножения на tK +1tK +2 и группировки членов)

получим

tK +2 P′ + 2(tK +2 + tK +1)PK′+2 + tK +1PK′+2 =
=	3	2	2


	tK +1tK +2	tK +2 (PK +2 − PK +1) + tK +2 (PK +1		− PK ) .

В этом уравнении только одно неизвестное – PK′+2 , то есть касательная в
точке соединения.
При проведении кривой через n				точек касательные во всех точках
соединения – P2′ Pn′−1			– определяются из следующего матричного уравнения:

t300

...

2(t2 + t3 )	t2	0
t4	2(t3 + t4 )	t3
0	t5	2(t4 + t5 )
...	...	...
...	...	tn

		3		2		2
					(P3	− P2 ) + t3	(P2
		t t t2			(P3	− P2 ) + t3	(P2	− P1)
		2 3
		3		2		2
					(P4	− P3 ) + t4	(P3
		t t t3			(P4	− P3 ) + t4	(P3	− P2 )
		3 4
		.........................................
		.........................................
	3		2			2
			tn−1	(Pn − Pn−1) + tn (Pn−1 − Pn−2
t	t		tn−1	(Pn − Pn−1) + tn (Pn−1 − Pn−2
	n−1	n

...

2(tn−1 + tn )

)

	P′
		1
		′
	P2
		′	=
	P3		=
...		...
tn−1
tn−1	Pn′

Это произведение матрицы размера (n − 2) n на матрицу n 1.

Результатом является матрица (n − 2) 1.

Система обычных уравнений, получающихся из этого матричного уравнения, будет определена, если известны, то есть касательные на концах кривой.

Решение этой системы даст значения касательных в точках соединения,

после чего могут быть получены коэффициенты Bi ,i =	1,	4	всех сплайновых
сегментов.
Для окончательного решения задачи построения		сплайн-кривой нам
остаётся выбрать пределы изменения параметра t в			каждом сегменте.

Поскольку все полученные формулы предполагают, что начало каждого сегмента соответствует t = 0, то необходимо определить лишь значения tK ,k = 2 n . Выбор этих величин будет влиять на гладкость сплайна.

Обычно эту задачу решают не из строгих соображений (например, обеспечение минимума кривизны вдоль всей кривой) – это довольно сложно. На практике приемлемыми являются простейшие методы выбора tK .

Можно, например, использовать так называемые нормализованные параметры, то есть считать, что на всех участках 0 < t <1.

Тогда матричное уравнение для определения касательных в точках соединения будет иметь вид:

											P′					3(P − P )
		1	4	1	0		0 ...	0	0	0	P′					3(P − P )
												1					3	1
		0	1	4	1		0 ...	0	0	0		′				3(P4 − P2 )
		0	1	4	1		0 ...	0	0	0		P2		=		3(P4 − P2 )			,
n−2					... ... ... ...				...			...		=			...		,
	... ... ...				... ... ... ...				...	...		...					...
		0	0	0	0		0 ...	1	4	1
		0	0	0	0		0 ...	1	4	1	Pn′				3(Pn −			Pn−1)

							n
а с учетом того, что P1′						и P2′ должны быть заданы:
												P′						− P )	− P′
		1	4	1	0		0 ...	0	0	0		P′					3(P	− P )	− P′
												2					3	1	1
		0	1	4	1		0 ...	0	0	0			′				3(P4		′
		0	1	4	1		0 ...	0	0	0		P3			=		3(P4	− P2 ) − P2		.
n−2					... ... ... ...				...						=			...		.
	... ... ...				... ... ... ...				...	...	...							...
		0	0	0	0		0 ...	1	4	1
		0	0	0	0		0 ...	1	4	1	Pn′−1					3(Pn − Pn−1) − Pn′

						n−2

Коэффициенты Bi ,i =1,4 для каждого сегмента вычисляются из следующего уравнения:

B4		2	−2	1
B	−3		3	−2
3	=	0	0	1
B		0	0	1
2			0	0
B1	1		0	0

1		P
		K
−1	PK +1		,1< k < n −1.
0		P
		K
0	PK +1

Такой метод удобен в вычислительном отношении, так как трехдиагональную матрицу из уравнения для PK′ ,k = 2,n −1 приходится обращать только один раз. На практике метод дает хорошие результаты, если точки P1,..., PK −1 расположены достаточно равномерно.

При неравномерном распределении точек в качестве t обычно выбирают расстояние между P и P – метод локальных хорд. Кубические сплайновые кривые широко распространены, однако имеют ряд недостатков. Например, с их помощью нельзя точно передать дугу окружности, а только приближенно.

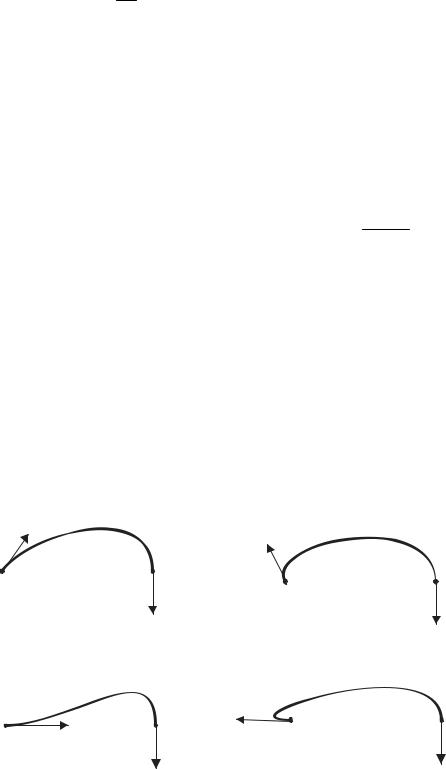
Примеры кубических сплайновых сегментов.

Рисунок 4.3

4.3КРИВЫЕ БЕЗЬЕ

Рассмотренные сплайн-кривые проходят через все заданные точки. Во многих случаях это дает хорошие результаты, однако имеется один недостаток

– необходимость явного задания касательных векторов. Интуитивно эти вектора трудно себе представить, особенно неподготовленному пользователю.

Более удобный способ построения кривых предложил Безье. Кривая Безье определяется несколькими точками, – так называемыми вершинами многоугольника. При этом кривой принадлежат лишь первая и последняя точки, а остальные задают ее форму.

Рисунок 4.4.

Так как вид кривой зависит то формы многоугольника, то изменение положения вершин создает y пользователя значительно более ясное интуитивное ощущение восприятия связи между вершинами, задаваемыми в диалоговом режиме, и требуемой формой.

Кроме того, если сплайн-кривые имеют фиксированный порядок (мы рассмотрели. Порядок равный трем – кубические сплайны), то в методе Безье порядок любого криволинейного сегмента может быть увеличен путем задания дополнительных вершин.

Математически кривая Безье описывается полиномиальной функцией, построенной в так называемом базисе Бернштейна. Базисная функция в нем задается соотношением

I	n,i	(t) = cn	ti (1−t)n−i ,
		i
где cni =		n!		,	0 <i < n .

		i!(n −i)!

Здесь n – степень полинома; i – порядковый номер отдельной вершины. Точки кривой в базисе Бернштейна задаются как

P(t) =

(t) , 0 < t <1

n,i

∑ i

i=0

то есть n – й порядок полинома характеризуется n +1– й вершиной.

В начальной точке t = 0

(0) =

00 (1−0)n−0 =1;(0!=1) ;

n,0

0!(n −0)!

(0) = 0,i =

(00 =1) .

n,1

1,n

В конечной точке t =1

In,n

(1) =

1n (1−1)n−n =1;

n!(n − n)!

In,1(1) = 0,i =

0,n −1

То есть P(0) = P0

и P(1) = Pn , вершины P0 и Pn действительно являются

началом и концом криволинейного сегмента.

В качестве примера рассмотрим кубические кривые Безье. Зададим

постоянные приращения параметру t :

t ={0;1 3;2 3;1}

Тогда

(t) =

t(1−t)2 = 3t(1−t)2 ;

3,1

1!2!

(t) =

t2 (1−t) =3t2 (1−t).

3,2

2!1!

Получим

I3,0

I3,1

I3,2

I3,3

1/ 3 8/ 27 4 / 9 2/ 9 1/ 27

2/ 3 1/ 27 2 / 9 4/ 9 8/ 27

То есть

P(0) = P0 ;

P(1 3) =8 27 P0 + 4 9 P1 + 2 9P2 +1 27P3;

P(2 3) =1 27 P0 + 2 9 P1 + 4 9P2 +8 27P3;

P(1) = P3 .

В зависимости от положения точек P0 P3 могут получаться различные кривые.

		P2
P1	P2	P3
		P3

Рисунок 4.5

При сопряжении двух сегментов требуется выполнить условия непрерывности в общем случае k – го порядка, то есть равенства k – й производной кривой первого сегмента в конечной точке и k – й производной второго сегмента в начальной точке.

Рассмотрим условие непрерывности первого порядка.

	′
Выражение для P (t) удобно найти, явно расписав сумму для P(t) :
P(t) = P C0t0	(1−t)n	+ PC1t1(1−t)n−1	+.. + P Cn−1tn−1	(1−t) + PnCnt(1−t)0		=
0 n		1 n	n−1 n		n n
= P (1−t)n + nPt(1−t)n−1 +.. + nP tn−1(1−t) + P tn.
0	1	n−1	n
Тогда
P′(t) = −nP (1−t)n−1		+ nP (1−t)n−1 − n(n −1)Pt(1−t)n−2			+.. +
0		1	1
+n(n −1)P tn−2 (1−t) − nP tn−1 + nP tn−1.
n−1		n−1	n

В точках t = 0 и t =1 получим

P′(0) = n(P1 − P0 ) ;

P′(1) = n(Pn − Pn−1) ;

<<< < Предыдущая 1 2 3 4 5 6 78 / 118 9 10 11 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
05.02.2023903.62 Кб4Комплект контрольно-измерительных материалов по дисциплине «Иностранный язык»..pdf
#
05.02.2023951.54 Кб5Композитные материалы.-1.pdf
#
05.02.20231.03 Mб6Композитные материалы..pdf
#
05.02.2023212.88 Кб4Компоненты электронных схем.-1.pdf
#
05.02.2023663.26 Кб5Компоненты электронных схем..pdf
#
05.02.2023634.52 Кб10Компьютерная геометрия и графика..pdf
#
05.02.2023465.43 Кб12Компьютерная графика. Лабораторные работы.pdf
#
05.02.20231.95 Mб6Компьютерная графика.-1.pdf
#
05.02.2023198.85 Кб5Компьютерная графика.-2.pdf
#
05.02.2023465.49 Кб6Компьютерная графика.-3.pdf
#
05.02.2023308.09 Кб15Компьютерная графика.-4.pdf