Компьютерная геометрия и графика

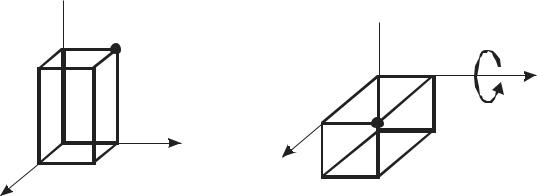
31

2.3ВРАЩЕНИЕ ВОКРУГ КООРДИНАТНЫХ ОСЕЙ

Вспомним, что на плоскости вращение вокруг оси, проходящей через начало координат и перпендикулярной плоскости, осуществлялось матрицей

Положительным направлением считается направление против часовой стрелки (если смотреть вдоль этой оси к началу координат!). В трехмерном случае вращение вокруг оси x

Y

Y

X

X Z

Z

Рисунок 2.2

то есть первая строка и первый столбец имеют вид [1 0 0 0]

Вокруг оси y −аналогично,

32

Y

Вокруг оси z

Y

X

Положительное направление по-прежнему определяется как направление против часовой стрелки, если смотреть вдоль оси, вокруг которой осуществляется вращение, к началу координат. Отметим, что в следствии некоммутативности умножения матриц при выполнении композиции вращения порядок преобразований существенен (в отличии от вращения на плоскости).

33

2.4 ОТОБРАЖЕНИЕ ОТНОСИТЕЛЬНО КООРДИНАТНЫХ ПЛОСКОСТЕЙ Отображение относительно плоскости x0y меняет лишь знак z

координаты точек. Таким образом,

2.5ПРОСТРАНСТВЕННЫЙ ПЕРЕНОС

Трехмерный линейный перенос изображения определяется выражением:

2.6ТРЕХМЕРНОЕ ВРАЩЕНИЕ ВОКРУГ ПРОИЗВОЛЬНОЙ ОСИ

В двумерном случае вращение вокруг произвольной оси осуществлялось путем композиции преобразований:

–переноса начала координат в точку пересечения оси вращения с плоскостью xy ;

–вращения вокруг оси;

–переноса начала координат в исходное состояние.

34

При этом ось вращения должна быть перпендикулярна плоскости xy .

Втрехмерном случае ставится задача вращения вокруг произвольной оси

втрехмерном пространстве. Как и для плоскости, метод заключается в последовательном выполнении переноса, вращения вокруг оси, проходящей через начало координат и обратного переноса.

– переноса начала координат в исходное состояние.

При этом ось вращения должна быть перпендикулярна плоскости xy .

Втрехмерном случае ставится задача вращения вокруг произвольной оси

втрехмерном пространстве. Как и для плоскости, метод заключается в последовательном выполнении переноса, вращения вокруг оси, проходящей через начало координат и обратного переноса.

При этом, однако, ось, проходящая через начало координат, может иметь произвольное направление.

Итак, если ось, вокруг которой выполняется вращение, проходит через

Определим элементы матрицы вращения R .

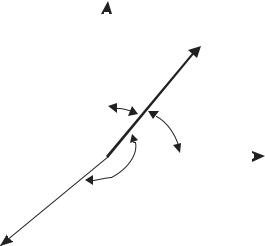
2.7 НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ МАТЕМАТИКИ Направление произвольной оси, проходящей через начало координат,

удобно определять через так называемые направляющие косинусы. Единичный вектор направления задается как

n = n1i + n2 j + n3k,

где n1 = cosα , n2 = cos β , n3 = cosγ

или в векторной форме

35

36

Направление nP перпендикулярно плоскости n0P . Теперь вернемся к получению элементов матрицы вращения R .

На рисунке 2.4 точка P преобразуется к точке P путем вращения вокруг оси n . Здесь

0P = 0P ; PQ = P Q ;

PQ 0P; P Q 0Q ; P S PQ .

Для получения элементов матрицы R необходимо координаты точки P выразить через координаты точки P , угол поворота θ –и направление оси вращения n .

Из рисунка видно

Из (3.7.3) следует QP = P −Q .

Далее

QS = QP cosθ = QP cosθ = P −Q cosθ .

Поскольку направление QS и QP совпадают, то

Длина вектора SP

SP = QP sinθ = QP sinθ = P −Q sinθ .

Направление вектора SP перпендикулярно плоскости Q0P , то есть

параллельно вектору nP .

Единичный вектор в этом направлении определяется соотношением

точки P , угол Q и вектор n .

Запишем этот результат в матричной форме;

39

2.8 АФФИННАЯ И ПЕРСПЕКТИВНАЯ ГЕОМЕТРИЯ Аффинная геометрия сохраняет параллельность линий и соотношения

между параллельными линиями. Аффинное преобразование является комбинацией линейных преобразований, сопровождаемых переносом изображения. Для аффинного преобразования последний столбец матрицы

4 ×4 должен быть равным [0 0 0 1]T . Композиция аффинных

преобразований также является аффинным преобразованием.

Вперспективной геометрии не сохраняется параллельность. Перспективное преобразование имеет место в том случае, когда последний столбец матрицы 4 ×4 не нулевой. Перспективными изображениями часто пользуются художники и архитекторы, так как эти изображения позволяют получить картину, близкую к реальности. Однако из-за сложности построения их редко используют конструкторы. Используя однородные координаты и матрицу преобразования 4 ×4 одинаково легко можно получать как аффинные, так и перспективные изображения.

Аффинное или перспективное преобразование в сочетании с построением проекции на некоторую плоскость образуют соответствующую (аффинную или перспективную) проекцию.

Вобщем случае проекции преобразуют точки, заданные в системе координат размерностью n , в точки системы координат размерностью m < n . В машинной графике рассматривают проекции точек трехмерного пространства в двухмерное (рисунок 2.5). Проекция трехмерного объекта (совокупности точек) строится при помощи прямых проецирующих лучей, которые называются проекторами, выходящими из центра проекции. Эти прямые проходят через каждую точку объекта; проекцией являются совокупность точек пересечения проекторов с проекционной плоскостью. При этом всегда проекцией отрезка является отрезок, поэтому достаточно спроецировать лишь граничные точки.

40

Отметим, что мы определили класс плоских проекций, то есть проекций на плоскость. Существуют еще проекции на криволинейную поверхность, но их мы рассматривать не будем.

В зависимости от расположения центра проекции, проекция бывает центральной (центр проекции удален от плоскости на конечное расстояние) и параллельной (центр в бесконечности).

проекторы проекционная плоскость

A

A’

центр проекции в бесконечности

Рисунок 2.5

Параллельная проекция является аффинной, а центральная – перспективной (по виду преобразования).

2.8.1 Аксонометрические проекции Аксонометрическая проекция получается с помощью преобразования,

определитель которого равен нулю. После выполнения преобразования осуществляется параллельное проецирование.

Существуют три вида аксонометрических проекций, различающихся по виду аффинного преобразования – ортогональная, диметрическая и изометрическая. Прежде чем остановиться на них, рассмотрим общую для всех этих видов часть – параллельное проецирование.