
Компьютерная геометрия и графика
..pdf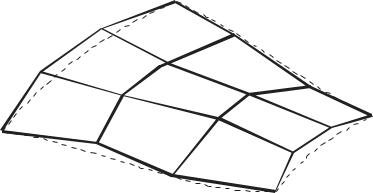
101
|
P41 |
|
|
P31 |
P42 |
|
|
|
|
|
|
P21 |
P32 |
|
|
|
P43 |
|
|
P22 |
P33 |
|
|
|
P23 |
P34 |
P44 |
|
|
P11 P24
P12
P13
P14
Рисунок 5.6
Кривые на этой поверхности могут быть получены фиксацией одного из параметров – u или w.
Например, при 0 ≤ u ≤1и w = w1 :
Q(u, w) = (1− u)3
P11 |
P12 |
P13 |
P21 |
P22 |
P23 |
|
|
P33 |
P31 |
32 |
|
P41 |
P42 |
P43 |
|
|
2 |
u |
3(1 |
− u)u |
2 |
u |
3 |
|
|
||
3(1− u) |
|
|
|
|||||||||
P |
|
(1− w )3 |
|
|
|
|
|
|
|
|||
14 |
|
3(1− w |
j 2 |
w |
|
|
|
|
|
|
|
|
P |
|
) |
j |
|
|
|
|
|
|
|||
24 |
|
j |
|
|
|
|
|
|
|
|||
P34 |
|
|
|
|
2 |
. |
|
|
|
|
|
|
|
3(1− wj )wj |
|
|
|
|
|
|
|
||||
P44 |
w3j |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
Здесь произведение двух последних матриц дает вектор – столбец точек характеристического многоугольника, определяющего кривую, то есть
|
Ρ11 |
Ρ12 |
Ρ13 |
Ρ14 |
||||
|
Ρ |
21 |
Ρ |
22 |
Ρ |
23 |
Ρ |
24 |
|
|
|
|
|
||||
|
Ρ31 |
Ρ32 |
Ρ33 |
Ρ34 |
||||
|
Ρ41 |
Ρ42 |
Ρ43 |
Ρ44 |
||||
|
||||||||
(1− w |
)3 |
P |
|
|||
3(1− w |
j |
|
|
1 |
|
|
)2 w |
P |
|
||||
|
j |
|
)w2 |
j |
= 2 |
|
|
3(1− w |
|
|
P |
|
|
|
w3j |
j j |
|
3 |
|
|
|
|
|
|
P4 |
||
|
|
|
|
|
|
|
Точки P1 P4 определяют кривую, причем точка P1 лежит на этой кривой и на кривой, граничной к поверхности при u = 0:
P1 = Q(0, wj ), точка P4 |
- на другой граничной кривой при u = 1: |
P4 = Q(1, wj ) , точки P2 |
и P3 лежат вне кривой и вне поверхности. |
Окончательное уравнение кривой на поверхности определяется как:
102
|
P1 |
|
Q(u,w ) = [(1− u)3 3(1− u)2 u 3(1− u)u2 u3 ] P2 |
. |
|
j |
|
|
P3 |
|
|
|
|
|
|
P4 |
|
При описании поверхности Безье матрица P не обязательно должна быть квадратной. Например, если характеристический многогранник имеет размерность 3 5, то
Q(u,w) = [(1− u)4 |
4(1− u)3u 6(1− u)2 u2 4(1− u)3 u4 ] |
||||||||
P |
P |
P |
|
|
|
|
|
|
|
11 |
12 |
13 |
|
(1− w) |
2 |
|
|||
P21 |
P22 |
P23 |
|
|
|
|
|||
P |
P |
P |
|
|
2(1− w)w |
|
. |
||
31 |
32 |
33 |
|
|
2 |
|
|
||
P41 |
P42 |
|
|
|
w |
|
|
|
|
P43 |
|
|
|
|
|||||
P |
P |
P |
|
|
|
|
|
|
|
51 |
52 |
53 |
|
|
|
|
|
|
|
Граничная кривая при u = 0 получится
|
|
|
|
|
(1− w)2 |
|
|
|
|
Q(0, w) = [ |
P |
P |
P |
] |
2(1− w)w |
|
или, что то же самое |
||
|
11 |
12 |
13 |
|
|
|
|
|
|
|
|
|
|
|
w |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Q(0, w) = [ |
|
|
|
|
|
|
P11 |
|
|
(1− w)2 |
2(1− w)2 w2 ] |
P |
|
. |
|||||
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
P13 |
|
|
|
|
|
|
|
|
|
|
||
Граничная кривая при u =1 |
|
|
|
|
|
||||
|
|
|
|
|
(1− w)2 |
|
|
|
|
Q(1, w) = [ |
P |
P |
P |
] |
2(1− w)w |
. |
|
|
|
|
51 |
52 |
53 |
|
|
|
|
|
|
|
|
|
|
|
w |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Остальные граничные кривые (при w = 0 и w =1) – аналогично.
103 |
|
|
|
|
P52 |
P53 |
|
P51 |
|
||
P42 |
|||
P41 |
|||
P31 |
|
|
|
P32 |
|
P43 |
|
P22 |
|
||
|
P33 |
||
P21 |
|
|
|
|
P12 |
P23 |
|
|
|
P11 |
|
P13 |
|
|
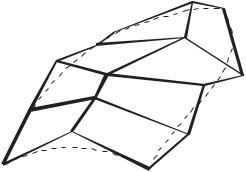
Рисунок 5.7
Поверхность 3×5 может быть предпочтительнее в том смысле, что изменение центральной точки повлияет на форму поверхности лишь в центре и не изменит наклоны в граничных точках.
В общем, виде поверхность Безье описывается выражением:
m n
Q(u,w) = ∑∑Pi+1, j+1Im,i (u)In, j (w),
i=0 j=0
где Im,i (u) = (Cmj )u j (1−u)m− j ,
In,i (w) - аналогично.
Характеристический многогранник для этой поверхности имеет размерность (m +1) ×(n +1) .
5.7 В-СПЛАЙН ПОВЕРХНОСТИ В-сплайн поверхности описываются выражением:
|
|
m |
m |
|
|
Q(u,w) = ∑∑Pi+1, j+1Ni,k (u)N j,i (w) |
|||
|
|
i=0 j=0 |
|
|
где |
Ni,1 |
|
1, |
åñëè ql ≤ u ≤ ql+1 |
(u) = |
0, |
в о ст альн ы х случаях |
||
|
|
|
||
N |
|
(u) = |
(u − qi )Ni,K −1(u) |
+ |
(qi+1 −u)Ni+1,K −1(u) |
|
i,K |
|
qi+K − qi+1 |
||||
|
|
qi+K −1 |
− qi |
|
||
|
|
|
|
|||
|
|
|
|
|
|
|
|
104 |
|
|
|
|
|
1, |
åñëè |
q ≤ w ≤ q |
|||
N j,l |
|
|
|
|
1 |
|
l+1 |
||
(w) = |
0, |
â î ñò àëüí û õ |
случаях |
||||||
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
N |
|
(w) = |
(w − qj )N j,l−1(w) |
+ |
(qj+1 − w)N j+1,l−1(w) |
. |
|||
i,K |
|
|
|||||||
|
|
|
qj+l−1 |
− qj |
|
|
qj+l − qj+1 |
||
|
|
|
|
|
|
||||
Здесь характеристический многогранник имеет разность (m +1)(n +1) с
учетом сложных вершин; k и l задают порядок в направления u и w соответственно.
105
Алфавитный указатель
А
Аксонометрические проекции 40, 41 Аффинная геометрия 39
В
Восстановление трехмерной информации 52 Вращение 15, 26 Вращение вокруг координатных осей 31
Д
Двумерное смещение 21 Диметрическая проекция 40, 43, 44, 46
И
Изменение масштаба 17, 23, 29 общее изменение масштаба 29, 30
покоординатное изменение масштаба 25, 29 Изометрическая проекция 46
К
Композиция преобразований 26 на плоскости 26
Кривые плоские кривые 56, 70
М
Матричные операции 5
106
О
Однородные координаты 21, 22, 25, 39 Ортогональная проекция 42, 52, 88 Отображение 16
отображение относительно координатных плоскостей 33
П
Перспективная геометрия 39 Перспективная проекция 47, 51, 52 Перспективное преобразование 39, 47, 48 Перспективные преобразования 48 Плоские кривые 56, 70
гипербола 67 окружность 58 парабола 65 эллипс 63
Поверхности 88 бикубическая поверхность 97
билинейные поверхности 94 В - сплайн поверхности 103
линейные поверхности Кунса 96 линейчатые поверхности 95 поверхности Безье 100 сферические поверхности 89
Преобразование сдвига 12, 30 Преобразования на плоскости 5
преобразование единичного квадрата 19 преобразование пересекающихся линий 14 преобразование плоских фигур 15
107
преобразование прямых линий 13 преобразование точек 8
Произвольная матрица вращения 2x2 20 Пространственные кривые 70
В-сплайны 81 кривые Безье 77
кубические сплайны 71 цилиндрическая спираль 70
Пространственный перенос 33
С
Сдвиг 10, 25, 29, 30
Т
Точки в бесконечности 25 Трехмерное вращение вокруг произвольной оси 33 Трехмерные преобразования 28
108
Рекомендуемая литература
1.Роджерс Д., Адамс Дж. Математические основы машинной графики. Пер. с англ./ Дэвид Ф. Роджерс, Дж. Алан Адамс; Пер. П.А.Монахов, Пер. Г.В.Олохтонова, Пер. Д.В.Волков. М.: Мир, 2001. - 605[3] с.:a-ил.
2.Роджерс Д. Алгоритмические основы машинной графики. М.: Мир, 1989 - 512 с.
3.Фоли Дж., Вэн Дем А. Основы интерактивной машинной графики. Кн. 1 и 2.
М.: Мир, 1985.
4.Павлидис Т. Алгоритмы машинной графики и обработки изображений. М.: Радио и Связь, 1986 - 400 стр.
5.Ростков А.А. Создайте анимацию сами. М.: ДИАЛОГ-МИФИ, 1995.
6.Ласло М. Вычислительная геометрия и компьютернаяграфика на С++ /Перевод с англ. М.: БИНОМ, 1997. - 304 с.: ил.
7.Корриган Дж. Компьютерная графика: Секреты и решения. М.: Энтроп, 1995. - 350 с.: ил.
8.Иванов В.П., Батраков А.С. Трехмерная компьютерная графика /Под ред. Г.М.Полищука. М.: Радио и связь, 1995. - 224 с.: ил.
9.Шикин Е.В., Боресков А.В. Компьютерная графика.Динамика, реалистические изображения. М.: "ДИАЛОГ-МИФИ", 1995. - 288 с.: ил.
