
Вариационные методы в механике
..pdfy' |
C1 |
|
dy |
|
C1 |
dy |
C1 |
dx y |
|
C1 |
dx C |
C1 |
C . |
||
|
|
|
|
x2 |
|
||||||||||
|
x2 dx x2 |
|
x2 |
|
2 |
x |
2 |
||||||||
|
|
|
|
|
|||||||||||
Экстремали y |
C1 |
C |
- семейство гипербол. |
|
|||||||||||
|
|
||||||||||||||
|
|
|
|
|
|
|
x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задача 5.
Найти экстремали функционала
b
J y ( y'2 2 yy' 16 y2 )dx .
a
Решение
Запишем уравнение Эйлера
F |
|
d |
F 0 . |
|
|
|
|
|
|
||
y |
|
|
|
|
|
|
|
||||
|
dx y' |
|
|
|
|
|
|
|
|||
В данном случае F y'2 |
2yy' 16y2 , тогда |
F |
2 y' 32 y, |
F |
2 y' 2 y. |
|
|||||
|
|
|
|
|
|
|
y |
|
y' |
|
|
Уравнение |
|
Эйлера |
|
принимает |
вид |
||||||
2 y' 32 y |
d |
(2 y' 2 y) 0 2 y' 32 y 2 y'' 2 y' 0 y'' 16 y 0. |
|
|
|||||||
dx |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Получили дифференциальное уравнение второго порядка с постоянными коэффициентами. Составим характеристическое уравнение
p2 16 0 p 4i корни чисто мнимые. Значит, |
решение надо искать в |
|
виде |
y a cos 4x bsin 4x. |
Проверим, |
y' 4a sin 4x 4b cos 4x, |
y'' 16(a cos 4x bsin 4x) 16y y'' 16y 0. |
|
Экстремаль имеет вид |
y a cos 4x bsin 4x, a,b - произвольные постоянные. |
|
Задача 6.
Найти экстремали функционала
1
J y (xy' y'2 )dx . Причем y(0) 1, y(1) 2.
0
Решение Запишем уравнение Эйлера
F |
|
d |
F |
0 . |
|
|
|
|
y |
|
|
|
|
|
|||
|
dx y' |
|
|
|
|
|
||
В данном случае F xy' y'2 . Тогда |
F |
0, |
F |
x 2 y'. |
||||
|
|
|
|
|
y |
|
y' |
|

Уравнение Эйлера принимает вид |
|
d |
(x 2 y' ) 0 x 2 y' |
C |
const. |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Отсюда y' |
|
1 |
(C x) dy |
|
1 |
(C x)dx y |
|
1 |
(C x)dx C |
|
1 |
(C x |
x2 |
|
)dx C . |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
2 |
1 |
|
|
|
2 |
|
1 |
|
|
|
|
|
|
|
|
2 |
|
|
1 |
2 |
2 |
|
|
1 |
2 |
|
|
|
|
2 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Экстремаль |
|
|
имеет |
вид |
|
|
|
y |
x2 |
|
|
1 |
C x C . |
|
Найдем |
C ,C |
|
из |
|
условия |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
4 |
|
2 |
|
1 |
|
|
2 |
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||
y(0) 1, y(1) 2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
y(0) C C 1. y(1) |
1 |
|
1 |
C C 2 |
1 |
|
|
1 |
C 2 C 1 |
1 |
C 1 |
1 |
|
5 |
C |
5 |
. |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
2 |
2 |
|
4 |
|
2 |
|
1 |
2 |
|
|
|
|
|
4 |
|
2 |
|
1 |
2 |
2 |
|
1 |
|
|
4 |
|
4 |
1 |
2 |
|
|||||||||||
Значит y x2 5 x 1. 4 4
Задача 7.
Найти экстремаль функционала
1
J y ey' tgy'dx . Причем y(0) 1, y(1) 1.
0
Решение
Запишем уравнение Эйлера
F d F 0 .y dx y'
|
|
|
|
|
|
|
y' |
' |
|
|
|
F |
|
' |
|
|
В данном случае |
F e |
|
tgy |
. Значит |
|
|
0 . |
|
||||||||
|
y |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Уравнение Эйлера принимает вид |
|
d F |
0 |
F const C. |
|||||||||||
|
|
|
||||||||||||||
|
dx y' |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y' |
||
|
F |
ey' tgy' ey' |
1 |
|
ey' (tgy' |
1 |
) C y' const C . |
|||||||||
|
y' |
cos2 |
y' |
cos2 y' |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|||||
|
dy |
C dy C dx y C x C |
. |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|||||||||
|
dx |
1 |
1 |
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Находим y(0) C2 |
0 |
|
C2 0. y(1) C1 C2 1 C1 1. |
|||||||||||||
Окончательно, искомая экстремаль есть y x . |
|
|||||||||||||||
2. Обобщения основной задачи вариационного исчисления.
1. Необходимые условия экстремума функционалов, зависящих от нескольких функций.
Рассмотрим |
множество |
функций |
одной |
переменной |
||||
M y y(x), z z(x),..., x [a,b] , |
таких , что все функции |
из |
М |
|||||
удовлетворяют условиям |
|
|
|
|
|
|
|
|
|
y(a) y1, y(b) y2 |
|
|
|
|
|||
|
z(a) z1, |
z(b) z2 . |
|
|
|
(1) |
||
|
............................... |
|
|
|
|
|||
Введем функцию |
F(x, y(x), y (x), z(x), z (x)) , |
где |
y(x), z(x) |
- |
две |
|||
произвольные функции и построим интеграл |
|
|
|
|
||||
|
|
b |
|
|
|
|
|
|
|
J [ y, z] F (x, y(x), y (x), z(x), z (x))dx . |
|
|
|
(2) |
|||
a
Рис. 3. |
|
|
|
|
|
Рис.4. |
|
|
|||
Выражение (2) является функционалом, зависящим от двух функций |
|||||||||||
y(x), z(x) . Задача ставится так: найти две |
y y0 (x) и |
z z0 (x) для которых |
|||||||||
данный функционал (2) имеет экстремум. |
|
|
|
|
|
||||||
Решение задачи проводится совершенно аналогично тому как это |
|||||||||||
было сделано в §1. Пусть при |
|
|
|
y y0 (x) , z z0 (x) |
функционал (2) имеет |
||||||
экстремум. Рассмотрим |
J[ y0 αδy, z0 βδz] , где α |
и β - произвольные |
|||||||||
вещественные переменные, а δy(x) , δz(x) |
- произвольные функции. Так как |
||||||||||
J [ y0 , z0 ] есть экстремальное значение, то |
|
|
|
|
|
||||||
|
dJ [ y0 |
αδy, z0 |
] |
|
0, |
dJ [ y0 , z0 βδz] |
|
0 . |
|||
|
|
|
|||||||||
|
|
dα |
|
|
|
dβ |
|
|
|
||
|
|
|
|
|
α 0 |
|
|
|
β 0 |
||
|
|
|
|
|
|
|
|
|
|
||
Повторяя буквально рассуждения §1 находим

F |
d F |
0, |
F |
|
d |
F |
0 . |
(3) |
|||
|
|
|
|
|
|||||||
dx y |
z |
dx z |
|||||||||
y |
|
|
|
|
|
||||||
Полученные |
уравнения |
также |
называются |
уравнениями Эйлера- |
|||||||
Лагранжа. Чтобы найти искомые функции y y0 (x), z z0 (x) надо решить систему из двух дифференциальных уравнений второго порядка Эйлера-
Лагранжа (3). |
|
|
|
|
|
Уравнения (3) можно обобщить на случай, |
когда |
функционал |
|||
зависит от произвольного числа |
функций |
y1(x), y2 (x),..., yn (x) . |
Рассмотрим |
||
функционал |
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
J [ y1,..., yn ] F (x, y1(x),..., yn (x), y1(x),..., yn (x))dx . |
|
||||
a |
|
|
|
|
|
Условия экстремума записываются в форме |
уравнений Эйлера- |
||||
Лагранжа |
|
|
|
|
|
F |
d |
F 0, |
i 1, 2,..., n |
|
|
|
|
|
|||
y |
dx y |
|
|
|
|
i |
|
i |
|
|
|
2. Необходимые условия экстремума функционала, зависящего от функции нескольких переменных.
Рассмотрим множество функций |
f (x1, x2 ) , |
зависящих от двух |
||
переменных x , x |
2 |
, изменяющихся в некоторой области G на плоскости 2. |
||
1 |
|
|
|
|
Пусть кривая C - является границей данной области |
G . |
|||
|
|
|
|
|
|
Рис.5. |
|
|
|
|
|
|
|
Предположим, что все рассматриваемые |
функции f (x1, x2 ) |
||||||||||||
принимают одинаковые |
|
значения |
на границе |
|
|
C |
области |
G . Введем |
|||||
функцию F(x , x , f (x , x ), f |
x |
(x , x ), f |
x |
(x , x )) , где |
f |
x |
|
f (x1, x2 ) , f |
x |
|
f (x1, x2 ) |
||
1 2 |
1 2 |
1 2 |
|
1 2 |
|
|
x1 |
|
x2 |
||||
|
|
1 |
|
2 |
|
|
|
1 |
|
2 |
|||
|
|
|
|
|
|
|
|
|
|||||
и построим двойной интеграл

J [ f ] F(x1, x2 , f (x1, x2 ), f x1 (x1, x2 ), f x2 (x1, x2 ))dx1dx2 . |
(4) |
|
G |
|
|
Задача ставится так: из всех функций |
f (x1, x2 ) |
найти такую |
функцию f0 (x1, x2 ) для которой функционал (4) |
принимает экстремальное |
|
значение. Решение осуществляется также как и в §1. Мы рассматриваем
J [ f0 αh] , где α - вещественная |
переменная, а h(x1, x2 ) |
- произвольная |
|||||||||||||||||||||||||||||||
фиксированная функция. Условие экстремума имеет вид |
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
dJ [ f0 αh] |
|
|
|
|
0 . |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
dα |
|
|
|
|
|
α 0 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Но J [ f αh] F(x1, x2 , f αh, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
fx1 αhx1 , fx2 |
αhx2 )dx1dx2 . Значит |
|
|||||||||||||||||||||||||||||||
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
dJ [ f αh] |
|
|
|
|
F |
|
|
|
|
F |
|
|
|
|
|
F |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
|
hx1 |
|
|
|
|
hx2 |
dx1dx2 . |
|
|||||||
|
|
dα |
|
|
|
α 0 |
f |
|
fx1 |
|
|
fx2 |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
F |
|
|
|
|
|
|
|
|
|
F |
|
|
|
|
|
F |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Рассмотрим |
|
|
|
h |
dx dx |
|
|
|
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
h |
|
dx dx |
. |
|||||||
f |
|
|
x |
|
|
|
|
|
|
|
x f |
|
|
||||||||||||||||||||
|
x1 |
|
|
1 2 |
|
f |
|
|
|
|
|
|
|
|
|
1 2 |
|
||||||||||||||||
|
G x1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
x1 |
|
|
|
|
|
1 x1 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Тогда
dJ [ f αh] |
|
|
|
F |
|
F |
|||
|
|
|
|||||||
|
|
|
|
||||||
|
|
|
|
|
|
|
|||
dα |
f |
x1 |
|
fx1 |
|||||
α 0 |
|
|
|
||||||
|
|
|
G |
|
|
|
|
|
|
x2
F |
|
|
|
|
|
|
|
F |
|||
hdx dx |
|
|
|
|
|||||||
|
x |
f |
|
||||||||
f |
|
|
1 2 |
|
|
|
|
||||
|
x2 |
|
|
|
G |
1 |
|
|
x1 |
||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
F |
|
h |
|
|
|
|
|
|
x |
|
f |
|
|||
|
|
2 |
|
x2 |
||
|
|
|
|
|
||
h dx dx
1 2
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
N |
|
|||
|
Второй интеграл имеет вид |
|
|
|
|
|
|
|
|
|
dx1dx2 . |
|||||||||
|
|
|
x1 |
x2 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
G |
|
|
|||||
Грина |
его |
|
можно |
|
|
записать |
|
|
|
|
как |
|||||||||
M |
F |
h(x , x ), |
|
N |
F |
h(x , x ) . |
|
На границе C : |
||||||||||||
|
|
|
||||||||||||||||||
|
1 |
2 |
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
||||
|
fx |
|
|
|
|
|
fx |
|
|
|
|
|
|
|
|
|
|
|
||
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x1, x2 ) |
|
C |
( f (x1, x2 ) αh(x1, x2 )) |
|
C |
h(x1, x2 ) |
|
C |
0 . |
||||||||||
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
M C N C 0 .
Используя теорему
Mdx2 Ndx1 .
C
Но тогда
Остаются
Так как
|
|
|
|
|
|
|
|
|
F |
|
|
F |
|
|
|
|
|
F |
|
|||||||||||
|
dJ [ f αh] |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h(x1, x2 )dx1dx2 . |
||||||
|
dα |
|
|
|
|
|
f |
x |
|
|
f |
|
|
|
|
x |
|
f |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
α 0 |
|
|
G |
|
|
|
|
1 |
|
|
|
x1 |
|
2 |
|
|
x2 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
dJ [ f αh] |
|
|
0 |
|
и |
|
|
h(x1, x2 ) - произвольно, находим |
||||||||||||||||||||||
|
dα |
|
|
α 0 |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
F |
|
|
|
|
F |
|
|
|
|
|
|
F |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 . |
|
|
|
(5) |
|||
|
f |
|
x |
|
f |
|
|
x |
f |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
x1 |
|
|
|
x2 |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||
Полученное дифференциальное уравнение в частных производных также называется уравнением Эйлера-Лагранжа. Чтобы найти искомую функцию f0 (x1, x2 ) надо решить уравнение Эйлера-Лагранжа (5).
Уравнение (5) можно обобщить на случай, когда функционал зависит от функции любого числа переменных. Рассмотрим функционал
J [ f ] .G. .. F(x1, x2 ,..., xn , f (x1, x2 ,..., xn ), fx1 ,..., fxn )dx1...dxn , где G - область в пространстве n.
Условия экстремума записываются в виде уравнений ЭйлераЛагранжа
|
|
|
|
|
F |
n |
|
|
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 . |
|
|
|
|
|
|
|
f |
x |
f |
|
|
|||
|
|
|
|
|
|
i 1 |
i |
|
xi |
|
|
|
Задача 1. |
|
|
|
|
|
|
|
|
|
|
||
Найти экстремали функционала |
|
|
|
|
|
|
|
|||||
J y1, y2 |
b |
|
|
|
|
|
|
|
|
|
|
|
( y1'2 (x) y2'2 (x) y1' (x) y2' (x) y1 (x) y2 (x))dx . |
|
|
||||||||||
|
|
a |
|
|
|
|
|
|
|
|
|
|
Решение |
|
|
|
|
|
|
|
|
|
|
||
Данный функционал зависит от двух функций y1(x) |
и y2 (x) . Функция |
|||||||||||
F(x, y , y , y' |
, y' ) |
в |
данном |
|
|
случае |
имеет |
вид |
||||
1 |
2 |
1 |
2 |
|
|
|
|
|
|
|
|
|
F(x, y1, y2 , y1' , y2' ) y1'2 y2'2 y1' y2' y1 y2 .
Запишем систему уравнений Эйлера
|
F |
|
|
|
d F |
0 , |
F |
|
d F |
0. |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
y |
|
dx y' |
y |
dx y' |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
1 |
|
|
|
|
|
1 |
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||
Имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
F 1, |
F 2 y' |
y' |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
y |
|
|
|
|
|
y' |
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F |
1, |
|
F |
2 y |
' y |
' . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
y2 |
|
|
|
|
y2' |
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Поэтому уравнения Эйлера имеют вид |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
1 |
d |
(2 y' y' |
) 0, |
1 |
d |
(2 y' |
y' ) 0, |
то есть |
d |
(2 y' |
y' |
) 1, |
d |
(2 y' |
y' |
) 1. |
|||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
dx |
1 |
2 |
|
|
|
|
|
dx |
2 |
1 |
|
dx |
1 |
2 |
|
dx |
2 |
1 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Интегрируя обе части, получим |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
2 y' y' |
x C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
1 |
2 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
y' |
x C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
2 y' |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
2 |
1 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
C1,C2 - произвольные постоянные. Получили систему из двух линейных уравнений
для нахождения y1' , y2' . Из этой системы находим
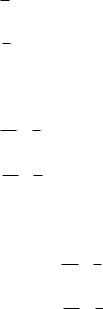
y1' 13 (x 2C1 C2 ), y2' 13 (x 2C2 C1).
Интегрируя обе части, найдем
y1 x2 1 (2C1 C2 )x C3 , 6 3
y2 x2 1 (2C2 C1)x C4 , 6 3
С1,С2 - произвольные коэффициенты.
y1 x2 1 (2C1 C2 )x C3 ,
Ответ: 6 3
y2 x2 1 (2C2 C1)x C4. 6 3
Задача 2.
Найти экстремали функционала
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
J y1, y2 , y3 ( y1'2 y2'2 y3'2 y1' y2' |
|
y1' y3' y2' y3' )dx . |
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Данный |
|
функционал |
зависит |
от |
|
трех |
функций y1(x) , y2 (x) , y3 (x) . |
|||||||||||||||||||||||||||||
Соответствующая функция F(x, y , y , y , y' , y' |
, y' |
) в данном случае имеет вид |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
3 |
1 |
2 |
3 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
F (x, y1, y2 , y3 , y1' , y2' , y3' ) ( y1'2 y2'2 y3'2 y1' y2' |
y1' y3' y2' y3' . |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Запишем систему уравнений Эйлера |
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
F |
|
d |
F |
0 , |
|
F |
|
|
d F |
0, |
|
F |
|
d F |
0. |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
y |
dx y' |
|
y |
dx y' |
|
|
|
dx y' |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|||||||||||||||||||||||
1 |
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
|
3 |
|
|
|
|
||||||
Имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
F |
0, |
|
F |
0, |
|
|
F |
0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
y |
|
y |
2 |
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
1 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
F |
2 y' |
y' |
y' |
, |
F |
2 y' |
y' y' |
, |
F |
|
2 y' |
y' y' . |
|
||||||||||||||||||||||
|
y' |
y' |
y' |
|
||||||||||||||||||||||||||||||||
|
1 |
|
|
2 |
3 |
|
|
|
2 |
|
|
1 |
3 |
|
|
|
|
3 |
1 |
|
2 |
|
||||||||||||||
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|||||||
Поэтому уравнения Эйлера имеют вид |
|
|
|
|
||||||||||||||||||||||||||||||||
|
d |
(2 y' y' y' ) 0, |
|
|
d |
(2 y' |
y' |
y' ) 0, |
d |
(2 y' |
y' |
y' ) 0. |
||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
dx |
1 |
|
2 |
|
3 |
|
|
|
|
|
dx |
2 |
1 |
|
|
3 |
|
|
|
dx |
3 |
|
1 |
2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Отсюда

2 y1' |
y2' |
y3' |
C1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
y1' |
y3' |
C2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 y2' |
|
С1,С2 ,С3 |
- произвольные постоянные. |
|
|
|
||||||||||||||||||
2 y' |
y' |
y' |
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
3 |
1 |
2 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Получили систему из трех линейных уравнений для |
нахождения y' |
, y' |
, y' . |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
Решая эту систему, |
выразим |
y' |
|
из первого уравнения и подставим во |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
второе и третье. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
y' |
C 2y' y' . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
3 |
|
1 |
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
' |
' |
C1 |
' |
|
' |
|
|
|
|
|
|
|
' |
|
' |
C1 |
|
|
|
|
|
||
2 y2 |
y1 |
2 y1 |
y2 C2 |
|
|
y2 y1 C2 |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
) y' |
y' |
C |
|
|
|
|
|
|
y' |
y' |
C |
|
|
|
|||||
2(C 2 y' y' |
|
|
|
|
|
2C 4 y' 2 y' |
|
|
||||||||||||||||
|
|
1 |
1 |
2 |
|
1 |
2 |
3 |
|
|
|
|
|
|
1 |
|
1 |
2 |
1 |
2 |
3 |
|
|
|
|
' |
' |
|
|
|
|
|
y' |
|
1 |
|
(3C C |
|
C ), |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
1 |
|
4 |
|
|
1 |
|
3 |
|
|
|
|
|
|
|
|||
y2 y1 C2 C1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
y' |
2C C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
3y' |
|
' |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
1 |
2 |
|
1 |
3 |
|
|
y2 |
|
|
|
|
(3C2 |
C1 |
C3 ). |
|
|
|
|
|
|
|
||
|
|
|
4 |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Теперь можно найти y' . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y' |
C 2 y' y' |
1 |
(3C C C ). |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
3 |
|
1 |
1 |
|
2 |
4 |
3 |
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Окончательно
y1' 14 (3C1 C2 C3 ), y2' 14 (3C2 C1 C3 ),
y3' 14 (3C3 C1 C2 ).
Интегрируя обе части, получим y1 14 (3C1 C2 C3 )x C4 ,
y2 14 (3C2 C1 C3 )x C5 , y3 14 (3C3 C1 C2 )x C6.

y1(x) 14 (3C1 C2 C3 )x C4 , Ответ: y2 (x) 14 (3C2 C1 C3 )x C5 ,
y3 (x) 14 (3C3 C1 C2 )x C6.
Задача 3.
Показать, что уравнения второго закона Ньютона представляют собой уравнения Эйлера для функционала
|
t2 |
mr |
2 |
(t) |
|
( |
|
||
|
|
|
||
S r |
2 |
|
||
|
t1 |
|
||
|
|
|
|
|
t2
V (r(t))dt L(r(t), r (t))dt .
t1
Этот функционал называется действием. Функция L есть разность между
кинетической энергией частицы |
mv 2 |
и потенциальной энергией V (r ) . |
|
2 |
|||
|
|
Решение.
Данный функционал зависит от трех функций x(t) , y(t) , z(t) являющихся компонентами радиус-вектора r (t) , t - независимая переменная. При этом,
как обычно |
v r (t) |
dr (t) |
, |
r 2 v 2 v2 |
v2 |
v2 |
x2 |
y2 z2 .Здесь |
v2 |
, v2 |
, v2 - |
|
|||||||||||
|
|
dt |
x |
y |
z |
|
|
x |
y |
z |
|
|
|
|
|
|
|
|
|
|
|
||
компоненты |
вектора |
скорости |
|
v . |
Роль |
функции |
|||||
F(t, x(t), y(t), z(t), x(t), y(t), z(t)) играет |
|
|
|
|
функция |
||||||
L(r(t), r (t)) L(x(t), y(t), z(t), x(t), y(t), z(t)) . Запишем уравнение Эйлера
L |
d |
L 0 , |
L |
|
d |
L 0, |
L |
|
d |
L |
0. |
|
|||||||||
|
|
y |
|
z |
|
|
|||||||||||||||
x |
dt x |
|
|
dt y |
|
|
dt z |
|
|
|
|
||||||||||
|
|
|
L |
|
V , |
|
L |
V |
, |
L V |
, |
|
|
||||||||
Имеем x |
|
x |
|
y |
|
y |
|
z |
z |
|
|
|
|||||||||
|
|
|
L |
mx, |
L my, |
L mz. |
|
|
|
|
|||||||||||
|
|
|
x |
|
|
y |
|
|
z |
|
|
|
|
|
|
|
|||||
Поэтому уравнения Эйлера имеют вид |
|
|
|
||||||||||||||||||
V |
|
d |
|
(mx) 0, |
V |
|
d |
(my) 0, |
V |
|
d |
(mz) 0. |
|||||||||
|
|
z |
|
||||||||||||||||||
x |
|
dt |
|
|
|
|
y |
|
dt |
|
|
|
|
|
|
dt |
|
||||
Или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
mx V |
, |
my |
V , |
mz V . |
|
|
|
|
|||||||||||||
|
|
|
x |
|
|
|
y |
|
|
|
z |
|
|
|
|
||||||
Но |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V F , |
V F , |
V F , |
где F , F , F |
- компоненты вектора силы F . |
|||||||||||||||||
x |
|
|
x |
|
y |
y |
z |
|
z |
|
|
|
x |
y z |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Таким образом
mx Fx , |
my Fy , |
mz Fz . |
Но это ничто иное, как уравнения второго закона Ньютона.
Задача 4.
Найти экстремали функционала
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||
|
J y1, y2 ( y1' y2' |
|
y12 |
y22 )dx . |
|
|
|
|
|
|
|
||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Решение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Данный |
|
|
функционал |
|
зависит |
от |
двух |
функций y1(x) |
и y2 (x) . |
||||||||||||||||||||||||||
Соответствующая |
|
функция |
F(x, y , y , y' |
, y' |
) в |
данном случае |
имеет вид |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
1 |
2 |
|
|
|
|
F (x, y , y |
|
, y' |
, y' |
) y' y' |
|
1 |
y2 |
|
1 |
y |
2. . |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
1 |
|
2 |
|
1 |
2 |
|
|
|
1 |
|
|
2 |
2 |
|
1 |
2 |
|
2 |
|
|
|
|
|
|
||||||||
Запишем уравнения Эйлера |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
F |
|
d |
F |
0 , |
|
F |
|
|
d F |
0. |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
y |
dx y' |
|
y |
dx y' |
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
Имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
F |
y , |
|
F |
y' |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
y |
|
|
|
1 |
|
|
y' |
|
2 |
|
|
v cex |
de x , |
|
|
|
|
|
|
|
||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
F |
y |
, |
|
|
F |
|
y |
' . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
y2 |
|
|
|
2 |
|
|
|
y2' |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Поэтому получаем уравнения |
|
|
|
|
|
|
|||||||||||||||||||||||||||||
y |
d |
y' , |
|
|
y |
d |
|
y' . |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
1 |
|
dx |
|
|
2 |
|
|
|
|
2 |
|
dx |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
y y , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
2 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
y y |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Получили систему из двух линейных дифференциальных уравнений. Сложим эти уравнения, а затем вычтем, будем иметь
y y ( y y |
), |
|||
2 |
1 |
1 |
2 |
|
y y ( y y |
). |
|||
2 |
1 |
1 |
2 |
|
Обозначим |
u y1 |
y2 , |
v y1 y2 . Значит |
|
u u, |
|
|
|
|
|
|
|
|
|
v v. |
|
|
|
|
Решение первого |
уравнения |
есть u a cos x bsin x , решение второго |
||
уравнения |
есть v cex |
de x , |
где a,b, c, d - произвольные постоянные. |
|
Проверим что это действительно решения.
