
Комплексные и гиперкомплексные числа
..pdf
Томский государственный университет
систем управления и радиоэлектроники
М. А. Приходовский
«Комплексные и гиперкомплексные числа»
Учебное пособие
Томск
2013
УДК 511(075)
ББК 22.141
П77
Приходовский М.А.
Комплексные и гиперкомплексные числа: учебное пособие /
М.А. Приходовский - Томск: Изд-во «Иван Фёдоров», 2013. -
32с.
Впособии изложены действия над комплексными числами, вводятся некоторые из основных функций, которые в дальнейшем изучаются в курсе ТФКП, даны некоторые обобщения (гиперкомплексные числа).
© Приходовский М.А., 2013
© ТУСУР, 2013
2
Оглавление
Введение ………………………………………………........... 4
§1. Действительная ось и комплексная плоскость ………….. 5
§2. Умножение на комплексное число и сравнение с
действием линейного оператора в плоскости……………… |
9 |
§ 3. Тригонометрическая и показательная формы записи |
11 |
комплексного числа…………………………………………… |
|
§ 4. Умножение и деление в тригонометрической и |
14 |
показательной форме…………………………………………… |
|
§ 5. Степень и корень. Формула Муавра. Формула |
16 |
извлечения корня……………………………………………… |
|
§ 6. Логарифм комплексного числа. Задачи на вычисление |
19 |
логарифма ……………………………………………………… |
§7. Отображения (функции) и их графическое представление …………………………………………………. 22
§8. Дифференцируемость и аналитичность. Восстановление
аналитической функции по её действительной или мнимой части ……………………………………………………………. 25
§9. Обобщения комплексных чисел. Системы
гиперкомплексных чисел……………………………………… |
28 |
Литература …………………………………………………… |
32 |
3
Введение
В пособии подробно с примерами и иллюстрациями изложены действия над комплексными числами, вводятся некоторые из основных функций, которые в дальнейшем будут изучаться в курсе теории функций комплексного переменного,
даны некоторые обобщения - гиперкомплексные числа.
Пособие рассчитано как на студентов ММФ ТГУ,
изучающих основы данной темы, так и на студентов любых факультетов и специальностей ТУСУРа, изучающих курс высшей математики. Данное пособие также может представлять интерес для студентов как материал для самостоятельной работы, а также для преподавателей при планировании занятий по данной теме.
4

§ 1. Действительная ось и комплексная плоскость
При изучении числовых систем в школе становится привычным понятие «действительная ось», «действительные» («вещественные») числа. Но эта система чисел является неполной, так как не содержит корни некоторых, казалось бы,
простых уравнений, например x2 1 0. Если у квадратичного уравнения ax2 bx c 0 отрицательный дискриминант, то есть b2 4ac 0, то на действительной оси нет ни одного корня уравнения. Однако существует система условных, обобщённых чисел, где и такие уравнения тоже имеют решения. Они называются комплексными числами и геометрически соответствуют точкам на плоскости, а известная ранее действительная ось - это горизонтальная ось Ох в данной плоскости.
Корень  1 обозначили символом i и назвали «мнимой единицей», то есть имеет место равенство i2 1. На плоскости число 1 (действительная единица) соответствует точке (1,0),
1 обозначили символом i и назвали «мнимой единицей», то есть имеет место равенство i2 1. На плоскости число 1 (действительная единица) соответствует точке (1,0),
потому что расположено на оси Ох, так что вполне логично и легко запомнить, что мнимая единица соответствует точке (0,1), то есть находится на конце второго базисного вектора плоскости (и расположена на оси 0y). Любая точка плоскости, имеющая координаты (x, y), в векторной записи соответствует xe1 ye2 ,
где е1 и е2 - это базисные векторы, координаты которых (1,0) и (0,1). В комплексной плоскости первый базисный вектор соответствует 1, второй числу i, поэтому координаты произвольной точки плоскости будут иметь вид: x 1 y i , то есть их можно записать как x yi. Это число называется комплексным числом, записанным в алгебраической форме. (Куда ставить ударение в этом слове, не так важно, потому что даже на одной и той же кафедре одни математики говорят
5

кОмплексное, другие - комплЕксное число, окончательный вариант так и не установился).
Сложение и вычитание комплексных чисел определяется аналогично сложению и вычитанию векторов в плоскости. Сумма векторов (a,b)+(c,d) есть вектор (a+c, b+d). Если это записать с помощью обозначения базисных векторов, то
(ae1 be2 ) + (ce1 de2 ) = (a c)e1 (b d)e2 .
А в плоскости комплексных чисел это действие имеет вид:
(a bi) (c di) (a c) (b d)i .
С определением умножения также особых проблем не возникает, при умножении нужно сначала раскрыть скобки так же, как это делается в любом арифметическом выражении, а
затем |
учесть, |
что |
i2 1. |
Итак, |
(a bi) (c di) ac adi bci bdi2 , |
дальше эти |
четыре |
||
слагаемых надо перегруппировать, и выражение содержащее i2 ,
присоединяется к 1-му слагаемому, ведь i2 это действительное число (-1). Получаем (ac bd) (ad bc)i.
Число z a bi называется сопряжённым для z a bi.
Интересно, что при умножении двух сопряжённых чисел в ответе всегда получится действительное число:
zz =(a bi)(a bi)=a2 b2i2 abi abi= a2 b2 .
6

И этим свойством пользуются при делении комплексных чисел: нужно домножить числитель и знаменатель на число, сопряжённое знаменателю, чтобы знаменатель стал числом действительным
|
a bi |
= |
|
(a bi) (c di) |
= |
ac bd bci adi |
= |
|
|
||||||||||
|
c di |
(c di) (c di) |
|
c2 d2 |
|
|
|
||||||||||||
|
ac bd |
|
|
bc ad |
i |
|
|
|
|
|
|
|
|
|
|
|
|||
|
c2 d2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
c2 d2 |
|
|
|
|
|
|
|
|
|
|
|
||||||
Пример. Выполнить деление z |
2 3i |
. |
|
|
|
||||||||||||||
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 4i |
|
|
|
|||
Решение. z |
2 3i |
= |
2 3i |
|
1 4i |
= |
2 12 3i 4i |
= |
10 7i |
||||||||||
|
|
|
|
|
|
1 4i |
1 4i |
1 4i |
|
|
12 42 |
17 |
|||||||
Ответ: z = 10 7 i
17 17
Запомните полезную схему расположения точек на плоскости в зависимости от знака действительной и мнимой части. Она пригодится при изучении тригонометрической формы комплексного числа, чтобы правильно определять, в какой четверти находится та или иная точка.
7

Вычисление корней через дискриминант с помощью комплексных чисел можно проводить по известным для действительных чисел формулам, только надо учитывать, что
D<0, поэтому при вычислении квадратного корня из дискриминанта появится мнимая единица.
Пример. Решить уравнение x2 2x 2 0.
Решение. Находим D b2 4ac 4 8 4. Таким образом,
корни:
2 
 4 2
4 2 
 4
4
 1 2 2i 1 i .
1 2 2i 1 i .
2 2 2
Если подставить решение в исходное выражение и вычислить по правилам действий с комплексными числами, то можно проверить, что это и есть корни,
( 1 i)( 1 i) 2( 1 i) 2 (1 i i 1) 2 2i 2 0 ( 1 i)( 1 i) 2( 1 i) 2 (1 i i 1) 2 2i 2 0
Из формул нахождения корня через дискриминант,
следует, что если z является корнем уравнения, то и сопряжённое к нему число - тоже является корнем этого уравнения.
Пример. Найти корни уравнения x2 4x 20 0.
Решение. Находим D b2 4ac 16 80 64
Таким образом, корни:
4 
 64 4
64 4 
 64
64
 1 4 8i 2 4i .
1 4 8i 2 4i .
2 2 2
8
§ 2. Умножение на комплексное число и сравнение с
действием линейного оператора в плоскости
Рассмотрим умножение произвольного комплексного числа на фиксированное комплексное число (a bi) (x yi) =
(ax by) (ay bx)i .
Если поочерёдно рассмотреть координаты, то их преобразование эквивалентно линейному отображению в
плоскости:
x |
|
ax by |
, |
что равносильно умножению |
a |
b x |
, |
|||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
a |
|
|
|
y |
|
bx ay |
|
|
b |
|
y |
|
||||
таким |
образом, |
|
умножение на комплексное |
число |
|
a bi |
||||||
изменяет положение точек в комплексной плоскости в точности
так же, как линейный оператор, имеющий матрицу |
a |
b |
|||||
|
|
. |
|||||
|
|
|
|
|
|
a |
|
|
|
|
|
|
b |
|
|
Введём величину |
|
a2 b2 тогда |
a,b |
|
можно |
||
представить в таком виде: |
a cos , |
b sin для |
|||||
некоторого , ведь геометрически в этом случае |
a,b - |
катеты |
|||||
прямоугольного треугольника, 
 a2 b2 - его гипотенуза.
a2 b2 - его гипотенуза.
9
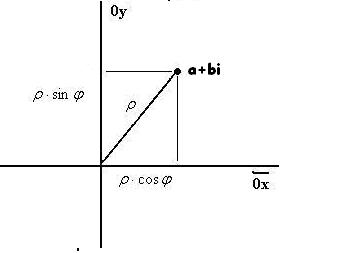
Абсцисса и ордината точки a,b это длины проекций на
две оси, они равны cos и sin соответственно. Кстати, |
|
эти величины |
и называются полярными координатами |
точки на плоскости. Итак, действие «умножение на
фиксированное комплексное число» |
соответствует линейному |
|||
оператору, |
задающему |
в |
плоскости |
растяжение |
пропорционально коэффициенту |
|
одновременно с поворотом |
||
на угол : |
|
|
|
|
|
|
cos |
sin |
|
|
|
|
|
|
|
|
|
|
|
|
|
sin |
cos |
|
В частности, умножение на i соответствует линейному |
||||
оператору с матрицей |
0 |
1 |
, то есть оператору поворота на |
|
|
|
|
||
|
|
1 |
|
|
|
|
0 |
|
|
90 градусов против часовой стрелки.
10
