
Математические модели динамических систем в форме уравнений для переменных состояния
..pdf
Пусть желаемые полюсы : λ1= -3, λ2= -2
Желаемый характеристический полином:
φ=(λ+3)(λ+1)= λ |
2+4 λ +3; α =4, α =3. |
||
|
|
1 |
2 |
Тогда k1 = a2 |
- α2 = 2 - 3 = -1, |
k2 = a1- α1 = -3 - 4 = -7. |
|
|
|
K = |-1 -7| |
|
Следовательно: v = u - x1 -7x2
Вычислив матрицу перехода P от исходной к нормальной форме
P = 1 −0.5 , 1 0
можно получить матрицу обратной связи для исходного представления системы: Kос = K.P.
41

Структура системы с ОС по переменным состояния
 -7
-7
u + v |
|
|
x2 |
|
x1 |
+ |
1 |
1 |
|||
|
|
p |
|
p |
|
3
 -2
-2
1
42
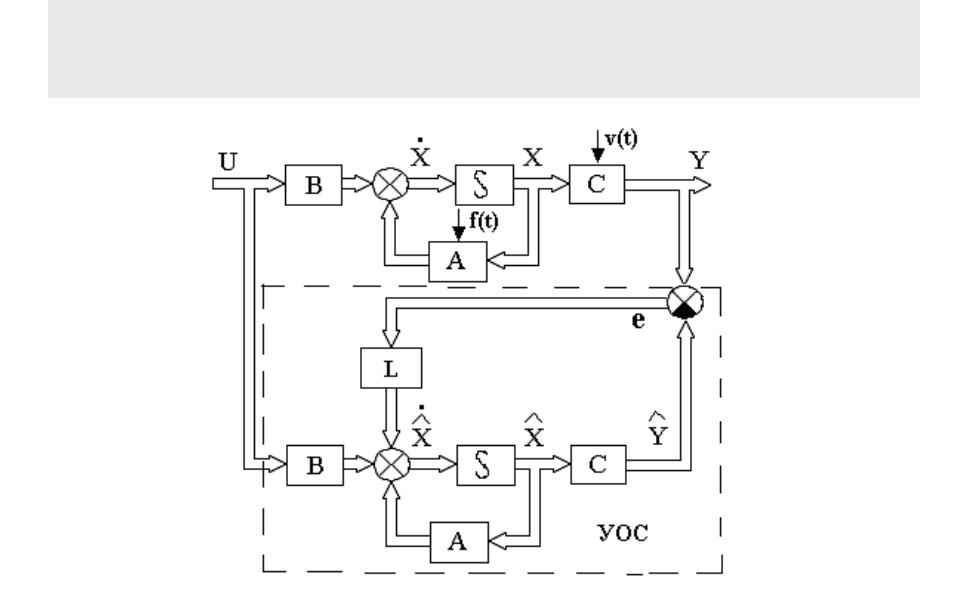
Оценивание вектора состояния
(наблюдатель Люенбергера)
43

Источниками ошибки e(t) являются начальное рассогласование, возмущение и помеха ( "шум" ) измерений.
Уравнение объекта:
Модель объекта:
Ошибка оценивания:
Выбором матрицы L можно обеспечить требуемое быстродействие и точность процесса оценивания.
44
