Министерство цифрового развития, связи и массовых коммуникаций

Российской Федерации Ордена Трудового Красного Знамени

федеральное государственное бюджетное образовательное

учреждение высшего образования

Московский технический университет связи и информатики

Кафедра «Теории электрических цепей»

Лабораторная работа №33

«Исследование активных интегрирующих и дифференцирующих цепей»

Москва 2021

Содержание

1. Цель работы 2

2. Ход работы 3

2.1. Предварительный расчет 3

2.2. Анализ интегрирующей цепи при синусоидальном воздействии 4

2.3. Анализ интегрирующей цепи при прямоугольном воздействии 5

2.4. Анализ интегрирующей цепи при треугольном воздействии 6

2.5. Анализ дифференцирующей цепи при синусоидальном воздействии 6

2.6. Анализ дифференцирующей цепи при прямоугольном воздействии 7

2.7. Анализ дифференцирующей цепи при треугольном воздействии 8

3. Вывод 9

4. Ответы на вопросы 9

1. Цель работы

С помощью машинного эксперимента получить форму напряжения на выходе активных интегрирующих и дифференцирующих цепей при различных формах напряжения на входе. Сравнить полученные характеристики с помощью программы Micro-Cap с аналогичными характеристиками, полученными расчётным путём.

2. Ход работы

   1. Предварительный расчет

Входное напряжение

u₁(t)=U_msin(2πft),- синусоидальное входное напряжение

где U_m=1 B- амплитуда входного напряжения;

f=2кГц- частота входного напряжения

t∈[0;1] мс- время

u₁(t) – прямоугольное входное напряжение

VZERO = 1 – минимальное значение, B;

VONE = 1 – максимальное значение, B;

P1 = 0 – начало переднего фронта, с;

P2 = 0 – начало плоской вершины импульса, с;

P3 = 0.25e-3 – конец плоской вершины импульса, c;

P4 = 0.25e-3 – момент достижения уровня VZEO, с;

P5 = 0.5e-3 – период следования импульсов, c;

U₁(t) – треугольное входное напряжение;

VZERO = -1, VONE = 1,

P1 = 0, P2 = 0.25e-3, P3 = 0.25e-3, P4 = 0.5e-3, P5 = 0.5e-3.

Для интегрирующей цепи

u₂(t)=K₁ ,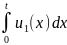

где u₂(t) - выходное напряжение;

K₁- коэффициент пропорциональности.

Для активной интегрирующей цепи

U₂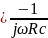 U₁- комплексный ток

Для дифференцирующей цепи

u₂(t)=K_{2 ,}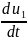

где u₂(t)- выходное напряжение

K₂- коэффициент пропорциональности

Для активной дифференцирующей цепи

U₂₌ -jωRCU₁

2.2. Анализ интегрирующей цепи при синусоидальном воздействии

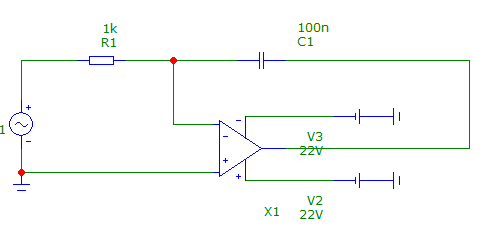
Рисунок 1 - Интегрирующая цепь при синусоидальном воздействии

На рисунке 2 представлен график зависимости напряжений на входе и выходе интегрирующей цепи от времени при синусоидальном воздействии.

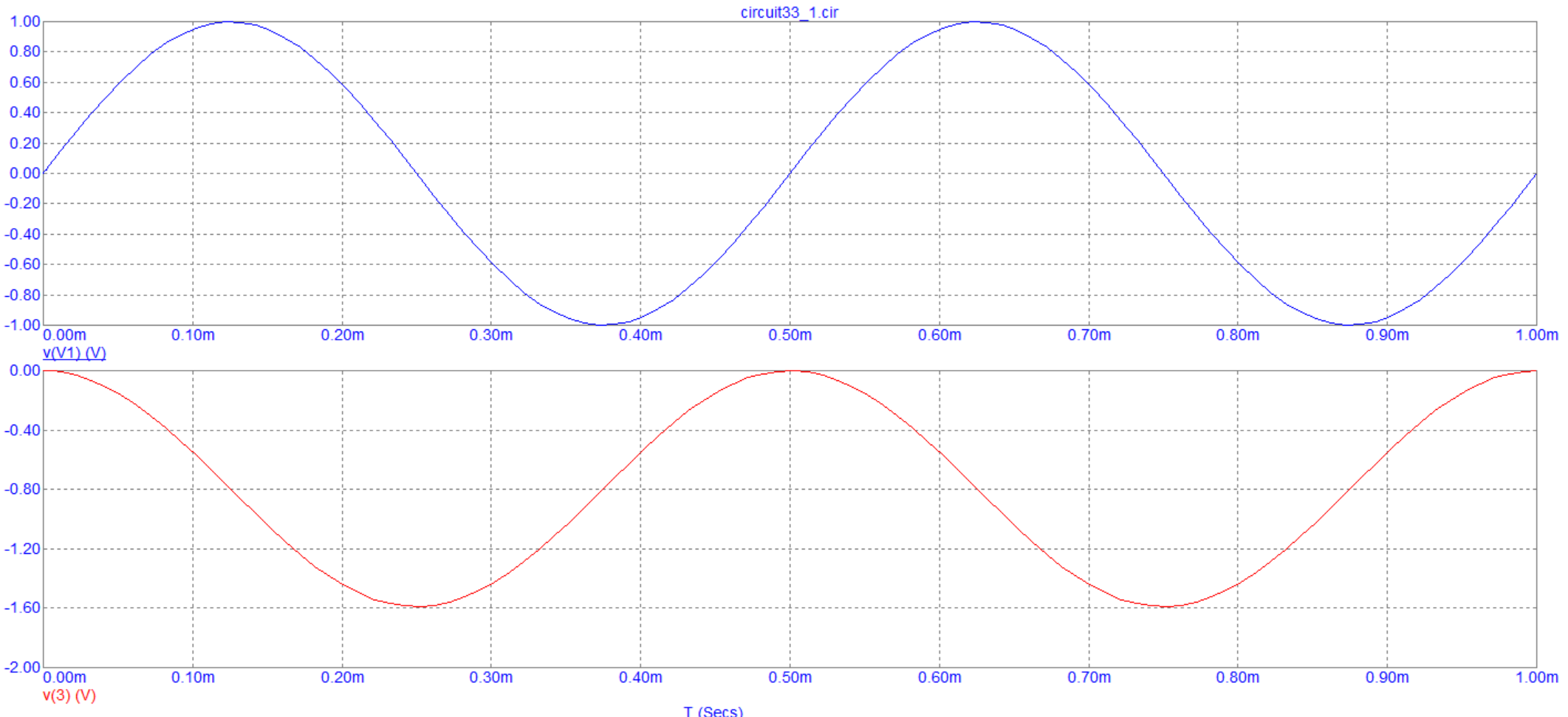
Рисунок 2 - График зависимости напряжений на входе и выходе интегрирующей цепи от времени при синусоидальном воздействии.

2.3. Анализ интегрирующей цепи при прямоугольном воздействии

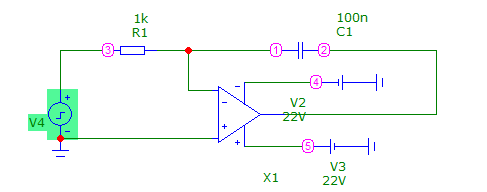
Рисунок 2 - Интегрирующая цепь при прямоугольном воздействии

На рисунке 3 представлен график зависимости напряжений на входе и выходе интегрирующей цепи от времени при прямоугольном воздействии.

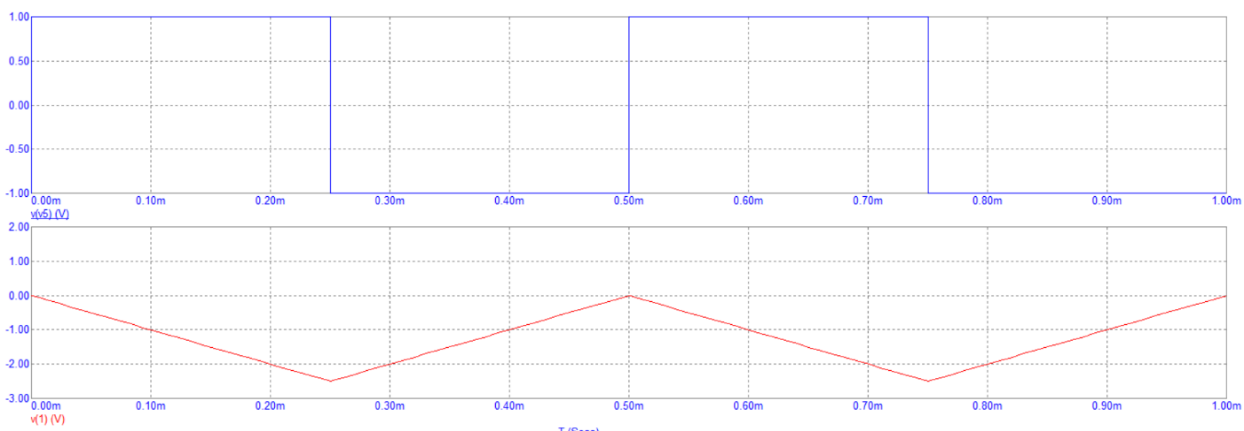
Рисунок 3 - График зависимости напряжений на входе и выходе интегрирующей цепи от времени при прямоугольном воздействии

2.4. Анализ интегрирующей цепи при треугольном воздействии

Рисунок 4 - Интегрирующая цепь при треугольном воздействии

На рисунке 5 представлен график зависимости напряжений на входе и выходе интегрирующей цепи от времени при треугольном воздействии.

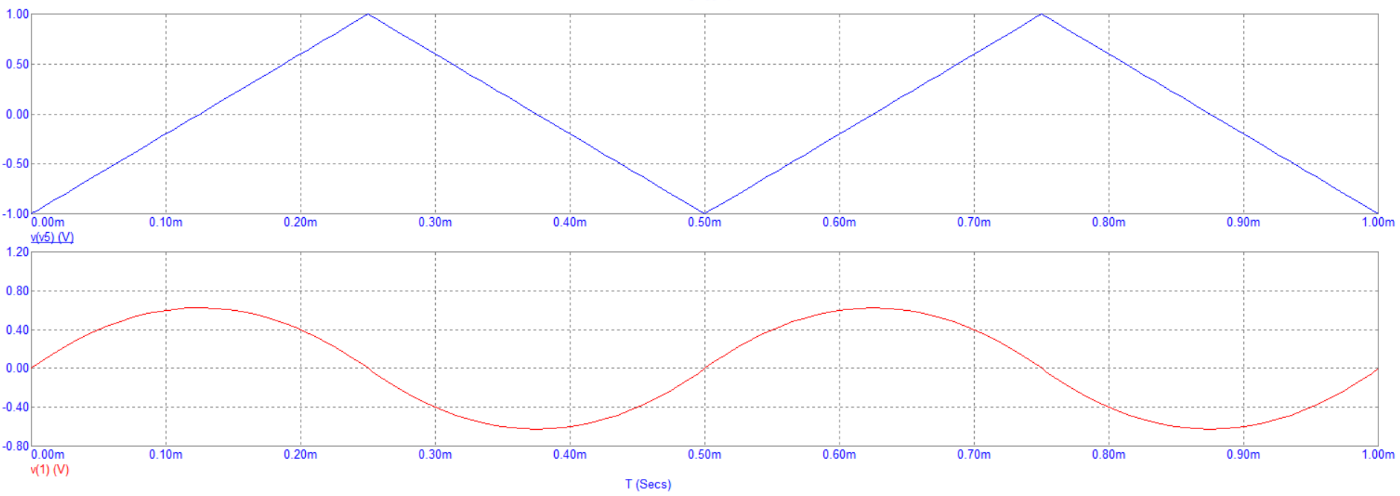
Рисунок 5 – График зависимости напряжений на входе и выходе интегрирующей цепи от времени при треугольном воздействии.

2.5. Анализ дифференцирующей цепи при синусоидальном воздействии

Рисунок 6 – Схема дифференцирующей цепи при синусоидальном воздействии

На рисунке 7 представлен график зависимости напряжений на входе и выходе дифференцирующей цепи от времени при синусоидальном воздействии.

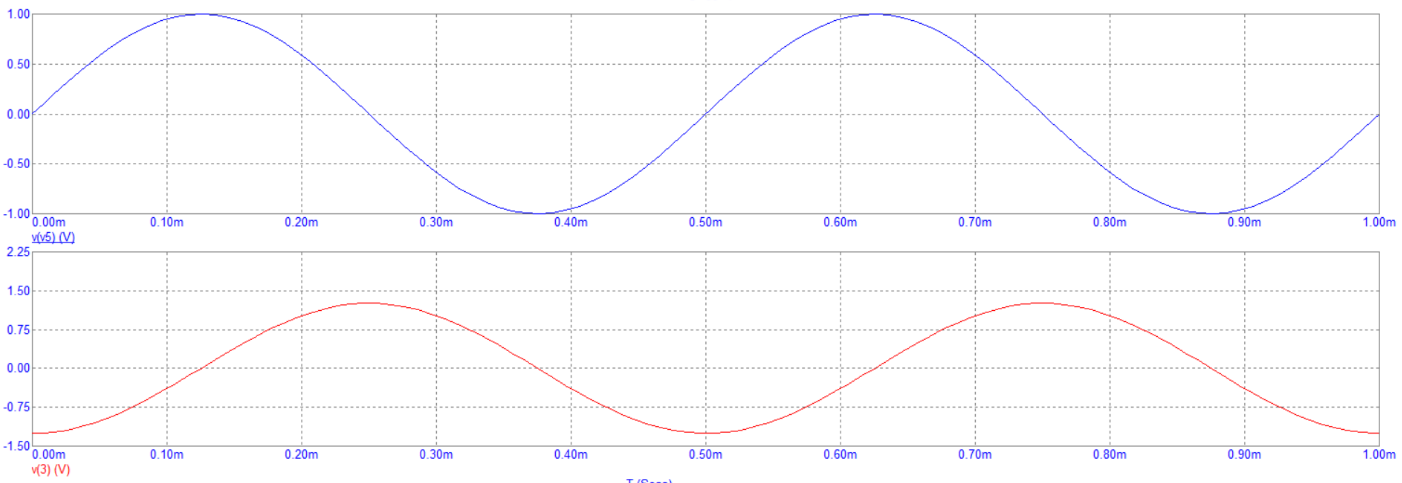
Рисунок 7 – График зависимости напряжений на входе и выходе дифференцирующей цепи от времени при синусоидальном воздействии.

2.6. Анализ дифференцирующей цепи при прямоугольном воздействии

Рисунок 8 – Схема дифференцирующей цепи при прямоугольном воздействии

На рисунке 9 представлен график зависимости напряжений на входе и выходе дифференцирующей цепи от времени при прямоугольном воздействии.

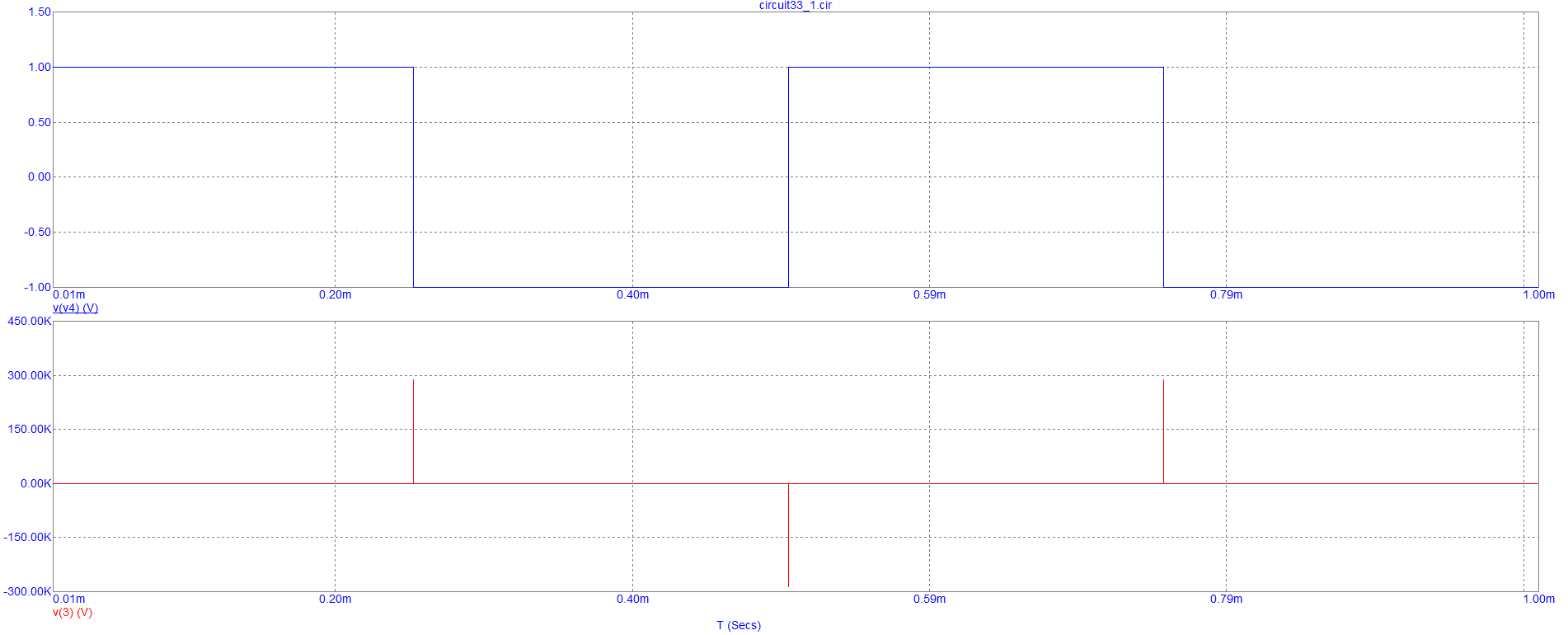
Рисунок 9 – График зависимости напряжений на входе и выходе дифференцирующей цепи от времени при прямоугольном воздействии.

2.7. Анализ дифференцирующей цепи при треугольном воздействии

Рисунок 10 – Схема дифференцирующей цепи при треугольном воздействии

На рисунке 11 представлен график зависимости напряжений на входе и выходе дифференцирующей цепи от времени при треугольном воздействии.

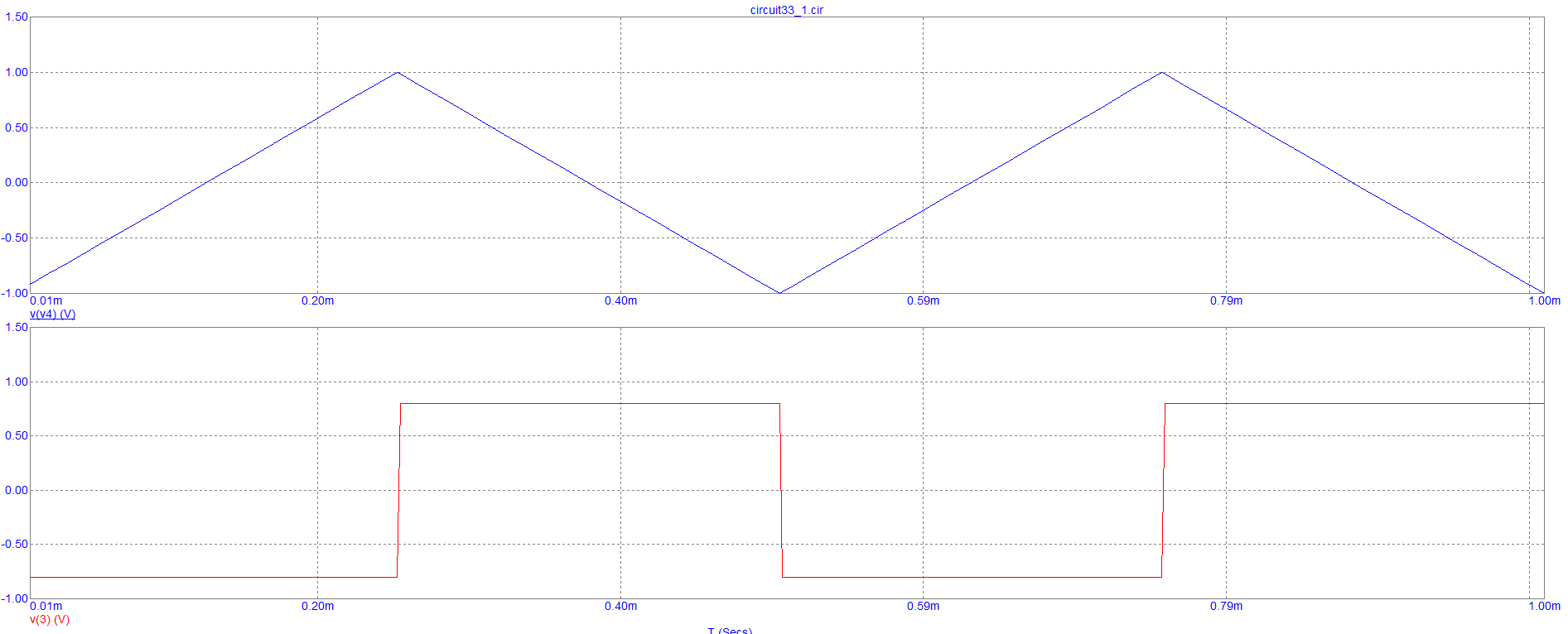
Рисунок 11 – График зависимости напряжений на входе и выходе дифференцирующей цепи от времени при треугольном воздействии.

3. Вывод

С помощью машинного эксперимента были получены формы напряжения на выходе активных интегрирующих и дифференцирующих цепей при различных формах напряжения на входе. Характеристики, полученные с помощью программы Micro-Cap, были сравнены с аналогичными характеристиками, полученными расчётным путём.

4. Ответы на вопросы

1. Какие цепи являются интегрирующими? Приведите пример.

Интегрирующие цепи – такие цепи, у которых выходное напряжение пропорционально интегралу входного напряжения. Примеры: Нелинейный интегратор, фильтр нижних частот, линии задержки сигналов.

2. Какие цепи являются дифференцирующими? Приведите пример.

Дифференцирующие цепи – такие цепи, у которых выходной сигнал прямо пропорционален производной входного сигнала. Пример: фильтр верхних частот.

3. В каких случаях применяются интегрирующие цепи?

Интегрирующие цепи применяют для выполнения операций интегрирования в аналоговых вычислительных устройствах.

4. В каких случаях применяются дифференцирующие цепи?

Дифференцирующие цепи применяют тогда, когда требуется преобразовать входное напряжение в сигнал, изменяющийся по закону производной входного напряжения.

5. Нарисуйте схему интегратора на ОУ и выведите его передаточную функцию Н?

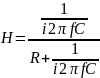
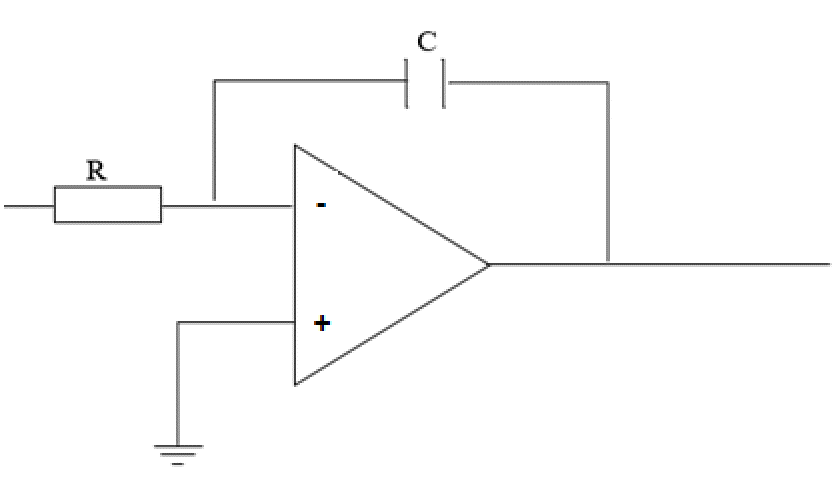
Рисунок 12 – Схема интегратора

6. Нарисуйте схему дифференциатора на ОУ и выведите его передаточную функцию Н?

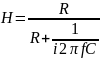
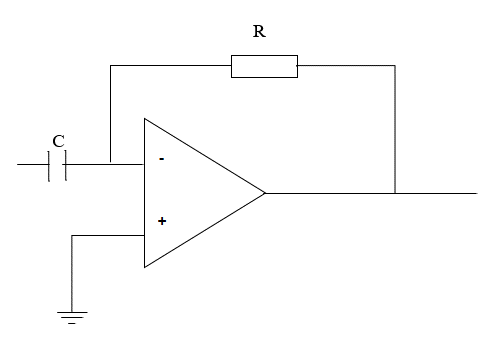
Рисунок 13 – Схема дифференциатора