
- •Практические занятия по физике
- •Часть 1
- •Учебное пособие
- •Краткие теоретические сведения и основные формулы
- •Величина полного ускорения
- •Поступательное движение
- •В случае равномерного вращательного движения угловая скорость
- •Алгоритм решения задач
- •Вращательное движение
- •Примеры решения задач
- •Решение
- •Решение
- •Уравнение движения при равноускоренном движении имеет вид
- •Решение
- •Решение
- •Задачи для самостоятельного решения
- •Краткие теоретические сведения и основные формулы
- •Выражение (2.5) можно записать в виде
- •Примеры решения задач
- •Решение
- •Решение
- •Решение
- •Подставив это выражение в уравнение (2), найдём
- •Решение
- •Подставляя численные значения, получаем
- •Решение
- •Решение
- •Задачи для самостоятельного решения
- •Занятие 3
- •Законы сохранения импульса и момента
- •Импульса. Энергия. Работа. Мощность
- •Контрольные вопросы для подготовки к занятию
- •Краткие теоретические сведения и основные формулы
- •Потенциальная энергия упруго деформированного тела
- •Полная механическая энергия:
- •Для переменного момента силы:
- •Примеры решения задач
- •Решение
- •Решение
- •Перепишем векторное уравнение (1) в скалярном виде
- •Кинетическая энергия начального положения тела
- •Решение
- •Подставив числовые значения, получим
- •Решение
- •Решение
- •Кинетическая энергия диска, вращающегося вокруг своей оси
- •Решение
- •Решение По закону сохранения энергии
- •Задачи для самостоятельного решения
- •Занятие 4
- •Краткие теоретические сведения и основные формулы
- •Примеры решения задач
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Тогда – плотность газа равна произведению массы одной молекулы на концентрацию молекул. Получим
- •Отсюда получаем изменение давления при утечке газа
- •Задачи для самостоятельного решения
- •Занятие 5
- •Явления переноса. Распределение молекул
- •По энергиям.
- •Контрольные вопросы для подготовки к занятию
- •Краткие теоретические сведения и основные формулы
- •Примеры решения задач
- •Решение
- •Решение Барометрическая формула
- •Задачи для самостоятельного решения
- •Занятие 6 первое и второе начала термодинамики Контрольные вопросы для подготовки к занятию
- •Краткие теоретические сведения и основные формулы Первое начало (закон) термодинамики выражает закон сохранения энергии:
- •На основании первого начала термодинамики
- •Адиабатный процесс
- •Работа, совершаемая газом при адиабатном процессе:
- •Теплоемкость одного моля и удельная теплоемкость при постоянном давлении:
- •Методика решения задач
- •I часть Примеры решения задач
- •Решение
- •Задачи для самостоятельного решения
- •II часть Примеры решения задач
- •Решение
- •Тогда работа
- •Вычислим
- •Решение
- •Решение
- •Задачи для самостоятельного решения
- •Занятие 7 закон кулона. Теорема остроградского – гаусса Контрольные вопросы для подготовки к занятию
- •Краткие теоретические сведения и основные формулы
Примеры решения задач
Задача
1. Груз массой
т
= 100 кг равномерно перемещают по
горизонтальной поверхности, прилагая
силу
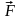 под углом
= 300
к горизонту. Коэффициент трения равен
0,3. Найти величину этой силы.
под углом
= 300
к горизонту. Коэффициент трения равен
0,3. Найти величину этой силы.
 Дано:
Решение
Дано:
Решение
= 300 Покажем все силы, действующие на тело на чертеже
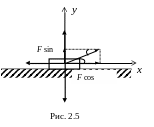 т
= 100 кг (рис. 2.5),
т
= 100 кг (рис. 2.5),
= 0,3
g = 9,8 м/с2
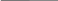 F
- ?
F
- ?
Так как тело движется равномерно, то по первому закону Ньютона, записанному в векторном виде, имеем
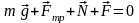 .
.
Чтобы решить задачу, надо записать это уравнение в скалярной форме. Для этого введем координатные оси ox и oy. На эти оси спроецируем силы, действующие на тело:
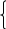 ox:
ox:
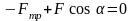 ;
(1)
;
(1)
oy:
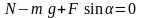 .
(2)
.
(2)
По определению, сила трения
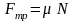 .
.
Из
уравнения (2) находим, что
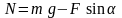 ,
поэтому
,
поэтому
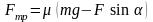 .
.
Подставляя последнее выражение в уравнение (1), получим
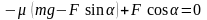 ;
;
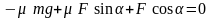 ;
;
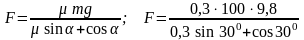 =
289 Н.
=
289 Н.
Ответ: F = 289 Н.
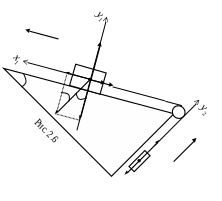
Задача 2. Груз массой 5 кг, связанный нерастяжимой нитью, перекинутой через неподвижный блок, с другим грузом массой 2 кг, движется вниз по наклонной плоскости. Найти натяжение нити и ускорение грузов, если коэффициент трения между первым грузом и плоскостью 0,1, угол наклона плоскости к горизонту 360. Массами нити и блока, а также трением в блоке можно пренебречь.
 Дано:
Дано:
m1 = 5 кг
m2 = 2 кг
= 0,1
= 360
g = 9,8 м/с2
а - ? T - ?
Решение
Сделаем рисунок и покажем все силы, действующие на тела и их ускорение, а также выберем системы координат, связанные с каждым телом в отдельности.
Запишем уравнение второго закона Ньютона для первого тела в векторной форме:
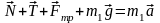 .
.
Проецируя это уравнение на выбранные направление осей x1 и y1, получим
 х1:
х1:
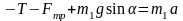 ;
(1)
;
(1)
y1:
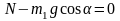 ;
(2)
;
(2)
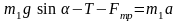 ;
(3)
;
(3)
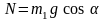 .
.
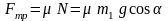 ,
подставим в выражение (3):
,
подставим в выражение (3):
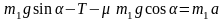 .
(4)
.
(4)
Запишем уравнение второго закона Ньютона для второго тела в векторной форме:
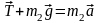 .
.
Спроецировав это уравнение на ось y2, получим
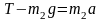 .
(5)
.
(5)
Решим систему уравнений (4) и (5):
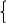 ;
;
.
Сложив почленно, получим
а
=
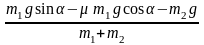 ;
;
а
=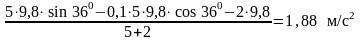 .
.
Cилу натяжения определим из уравнения (5):
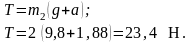
Ответ: a = 1,88 м/с2; T = 23,4 Н.
Задача 3. К концам невесомой и нерастяжимой нити, перекинутой через невесомый неподвижный блок, подвешены два груза массой по 100 г каждый. На один из грузов положен перегрузок массой 10 г. Найти силу, с которой перегрузок давит на груз, силу давления на ось блока, ускорение грузов и силу натяжения нити.
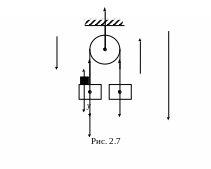

Дано:
m1 = m2 = 0,1 кг
m
=
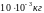
g = 9,8 м/с2
 F
- ?, Fд
- ?,
F
- ?, Fд
- ?,
a - ?, T - ?
4
