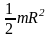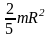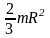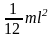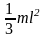Выражение (2.5) можно записать в виде

(2.6)

Векторная величина, равная произведению силы и времени ее действия называется импульсом силы ( 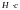). Импульс силы равен изменению импульса тела – второй закон Ньютона в импульсном виде.

III закон Ньютона: тела действуют друг на друга с силами, которые численно равны и направлены в противоположные стороны вдоль прямой соединяющей центры этих тел:

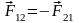. (2.7)

Сила возникает как при непосредственном контакте (давление прижатых друг другу тел, трения), так и через посредство создаваемых телами полей (поле тяготения, электромагнитное поле).

Сила трения – сила сопротивления, направленная противоположно относительному перемещению данного тела и приложенная по касательной к соприкасающимся поверхностям:

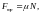(2.8)

где  – коэффициент трения скольжения, зависящий от свойств соприкасающихся поверхностей; N – сила нормального давления.

Сила, вызванная деформацией тел и препятствующая изменению объёма или формы тела, называется силой упругости.

При небольших деформациях растяжения или сжатие x сила упругости прямо пропорциональна деформации и направлена в сторону, противоположную ей (закон Гука):

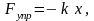(2.9)

где k – коэффициент упругости, зависит от свойств материала и геометрии деформируемого тела.

Закон Гука может быть записан в виде

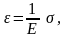(2.10)

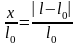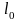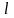где  = – относительная деформация; – длина тела до деформации (начальная длина); – длина тела после деформации; 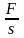 = – напряжение, возникающее в твердом теле, S – площадь сечения, на которую действует сила F; E – модуль Юнга.

Все тела притягиваются друг к другу. Для материальной точки (или шаров) закон всемирного тяготения имеет вид:

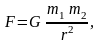(2.11)

где 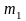и – массы тел, r – расстояние между материальными точками или центрами шаров; 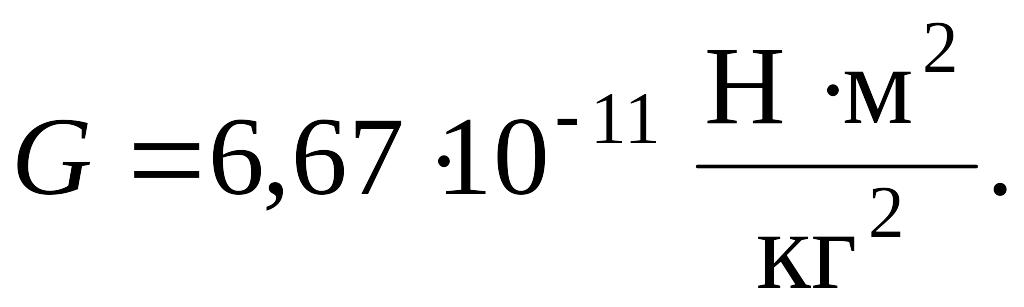– гравитационная постоянная.

Закон всемирного тяготения для тела находящегося у поверхности Земли

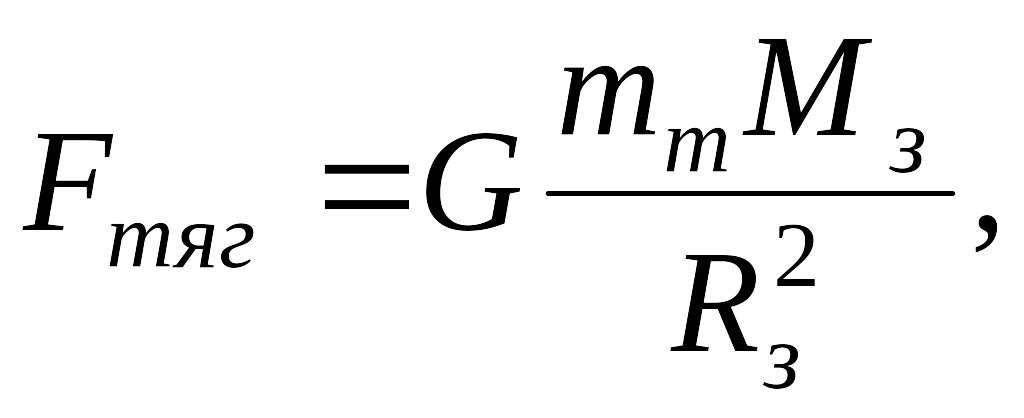
Если тело массой m находится над поверхностью Земли на высоте h, то на него действует сила тяготения

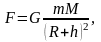(2.12)

где М – масса Земли, R = 6,37^.10⁶ м – радиус Земли.

Вес ( ) – это сила, с которой тело вследствие тяготения к Земле действует на опору (или подвес), удерживающую тело от свободного падения.

Эта сила равна лишь в том случае если тело и опора (или подвес) неподвижны относительно Земли.

В случае их движения с некоторым ускорением вес не будет равен . Состояние тела, при котором оно движется только под действием силы тяжести, называется состоянием невесомости.

Законы механики Ньютона справедливы и для вращательного движения. Но поскольку вращательное движение тела относительно оси может вызвать не любая сила, а только та, которая не проходит через ось вращения или не параллельна ей, то вводится понятие момента силы.

Моментом силы ( ) относительно оси называется векторное произведение радиуса вектора , проведенного из точки 0 в точку приложения силы , и силы .

.

Момент силы всегда перпендикулярен плоскости, в которой лежат и . Направление вектора определяется по правилу векторного произведения или по правилу правой руки: 4 согнутых пальца указывают направление, в котором сила вращает тело, а большой отогнутый направление – момента силы .

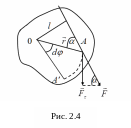Модуль момента силы (из геометрии) численно равен площади параллелограмма построенного на векторах и .

Тогда модуль момента силы , где – плечо силы – длина перпендикуляра, опущенного из точки 0 на линию действия силы . . _.

Если на вращающееся тело действует несколько сил, то результирующий, или главный момент всех внешних сил равен векторной сумме моментов сил, действующих на тело: 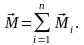Основным уравнением динамики вращательного движения является второй закон Ньютона.

Угловое ускорение, полученное вращающимся телом, прямо пропорционально суммарному (главному) моменту сил, действующих на это тело относительно оси вращения, и обратно пропорционально моменту инерции тела относительно этой же оси вращения:

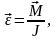
где J – момент инерции тела относительно оси вращения;  – угловое ускорение.

Момент инерции твёрдого тела равен сумме моментов инерции материальных точек, составляющих это тело:

,

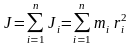
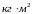где m_i – масса материальной точки; r_i – радиус вращения материальной точки.

Момент инерции тела характеризует инертность тела к изменению им угловой скорости под действием вращающего момента; момент инерции зависит от массы тела и её распределения относительно данной оси вращения.

Моменты инерции некоторых однородных тел вращения относительно заданных осей вращения приведены в табл. 2.1.

Т а б л и ц а 2.1

Тело	Положение оси вращения	J
Полый цилиндр (обруч)	Ось симметрии	J = mR2
Сплошной однородный цилиндр (диск)	Ось симметрии	J =
Сплошной однородный шар	Ось проходит через центр	J =
Сферическая оболочка	Ось проходит через центр	J =
Однородный тонкий стержень	Ось проходит через центр тяжести	J =
Однородный тонкий стержень	Ось проходит через конец	J =

Момент инерции J тела относительно любой оси вращения и момент инерции J₀ тела относительно оси, параллельной данной, и проходящей через центр инерции тела, связаны соотношением (теорема Штейнера)

J = J₀ + m d ²,

где m – масса тела; d – расстояние между осями.

Поскольку угловое ускорение 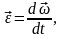то

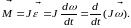
Произведение 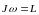называется моментом импульса тела.

Тогда

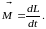
Отсюда следует вторая формулировка основного закона динамики вращательного движения: скорость изменения момента импульса со временем равна суммарному моменту сил, действующих на тело.