Квантово-механическая модель строения атома.

Электрон в атоме не движется по определённым траекториям, а может находиться в любой части околоядерного пространства: не существует вполне определенных круговых орбит электронов, электрон “размазан” в пространстве, подобно “облаку” отрицательного заряда. Размеры и форму электронного облака в заданном состоянии атома можно вычислить с помощью уравнения Шредингера (волновая функция). 

Электрон имеет двойственную природу (корпускулярно-волновую): обладает определенной массой и зарядом, т.е. ведет себя как частица, но в то же время проявляет волновые свойства, (характеризуется способностью к дифракции и интерференции). Для любой элементарной частицы справедливо уравнение (Луи де Бройль), связывающее параметры волны и частицы:

Принцип неопределенности Гейзенберга: микрочастица не может иметь одновременно определённую координату (x,y,z) и определённую соответствующую проекцию момента имплульса (p_x,p_y,p_z).

Магнитные свойства атома. Орбитальный и спиновый магнитные моменты. Полный магнитный момент. Эффект Зеемана.

Механический орбитальный момент импульса электрона связан с его орбитальным магнитным моментом следующим соотношением:

Помимо спинового механического момента, у электрона есть спиновый магнитный момент, который связан с механическим моментом соотношением:

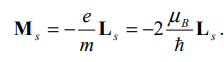
Полный магнитный момент электрона равен сумме векторов орбитального магнитного момента электрона и спинового магнитного момента:

Магнитный момент контура с током. Пусть по контуру с площадью S течет ток I. Величина P_m = I*S называется магнитным моментом контура с током. Магнитный момент контура с током — это вектор, который направлен перпендикулярно плоскости контура и связан с направлением тока правилом правого буравчика. Единицей магнитного момента в СИ является ампер на квадратный метр (А*м²).

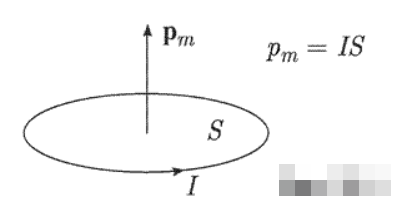
Магнитный момент является характеристикой не только контура с током, но и многих элементарных частиц (протонов, нейтронов, электронов и др.), ядер, атомов и молекул, определяя их поведение в магнитном поле.

Орбитальный магнитный момент электрона. Используя аналогию с контуром, вычислим магнитный момент, соответствующий орбитальному движению электрона (р_орб). Сила тока, соответствующая вращению электрона по круговой орбите, определяется формулой I = е/Т, где е — заряд электрона, Т - период его обращения. Так как период Т = 2πr/V (r — радиус орбиты, V — скорость электрона), то сила тока равна I = eV/2πr. Площадь контура — это площадь круга S=πr². Теперь можно рассчитать орбитальный магнитный момент электрона:

р_орб =IS = (eV/2πr)* πr²= eVr/2.

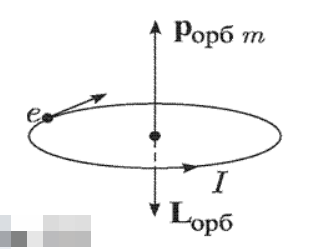
Орбитальный механический момент импульса электрона. В физических экспериментах обычно измеряют не сам орбитальный магнитный момент, а его отношение к другой характеристике орбитального движения — орбитальному механическому моменту импульса электрона.

L_орб = mVr, где m - масса электрона

Направления векторов L_op6 и р_орб показаны на рисунке.

Поскольку электрон — отрицательная частица, то его вращению по часовой стрелке соответствует «ток», текущий против часовой стрелки.

G_op6 = р_орб / L_op6 = е/2m (гиромагнитное отношение)

Спиновый магнитный момент электрона. Обнаружилось, что электрон, помимо орбитального момента импульса, обладает и собственным моментом импульса, который называется спином. Первоначально это связывали с вращением электрона вокруг собственной оси (отсюда и название спин — волчок). Позже выяснилось, что эта наглядная аналогия является очень грубой. Поэтому физики от нее отказались и считают спин неотъемлемой характеристикой элементарных частиц, присущей их природе. Со спином электрона (и других частиц) связан еще один магнитный момент, который называется спиновым магнитным моментом (р_cп). Для электрона отношение спинового магнитного момента к механическому спиновому моменту импульса вдвое больше, чем для орбитального движения:

G_cп = p_cп/L_cп = e/m

Множитель (фактор) Ланде (g-фактор). Формулы можно записать в обобщенном виде: p/L= g(e/2m). Для орбитального движения электрона он равен 1, для спина электрона он равен 2.

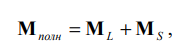
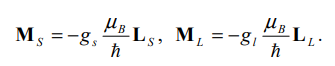
Модуль полного магнитного момента можно аналогично орбитальному и спиновому моментам записать в виде:

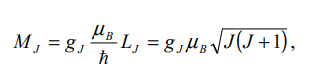
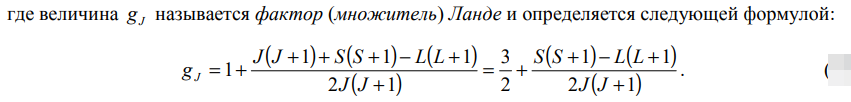
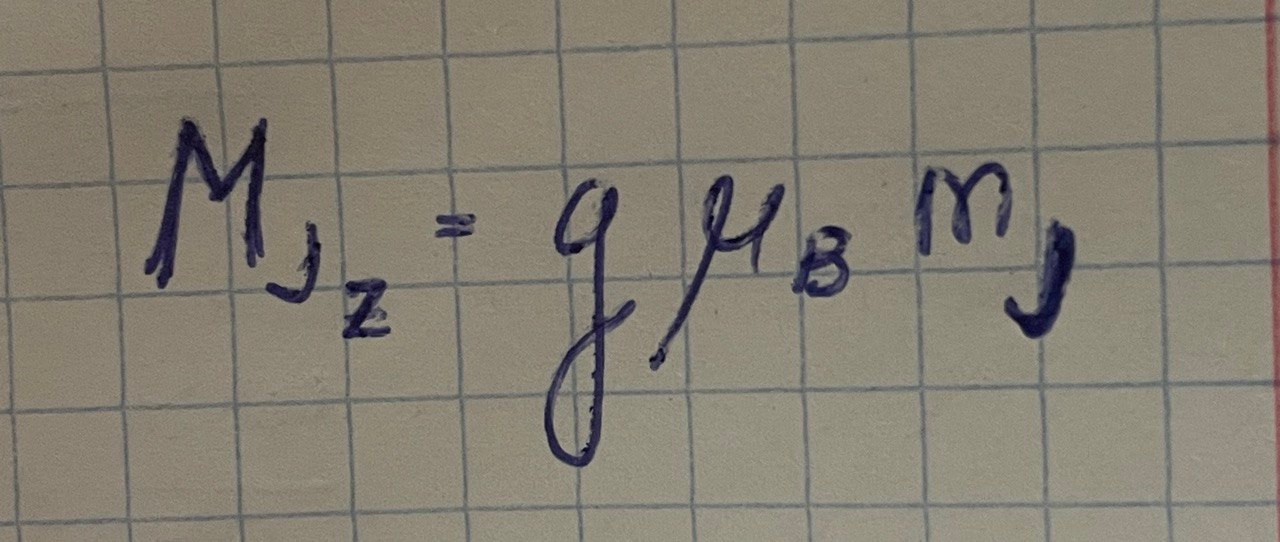
Иногда при факторе Ланде ставят «-». Это обусловлено тем, что заряд электрона -e.

Эффект Зеемана

Расщепление энергетических уровней электрона в магнитном поле.

Энергия атома в магнитном поле с учетом того, что в отсутствие поля энергия атома равна Е0, определяется формулой:

Так как магнитное квантовое число m_J может принимать 2J + 1 значений от +J до J, то следует, что каждый энергетический уровень при помещении атома в магнитное поле расщепляется на 2J +1 подуровней. Это схематически показано на рисунке для J = 1/2. Разность энергий между соседними подуровнями равна:

Е = g_БВ.

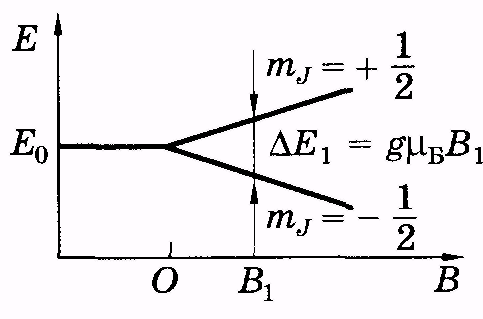
Расщепление энергетических уровней приводит и к расщеплению спектральных линий атомов, помещенных в магнитное поле. Это явление называют эффектом Зеемана.

Запишем выражение для двух подуровней Е₁ и Е₂, образованных при наложении магнитного поля:

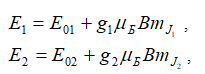
где Е₀₁ и Е₀₂ — энергетические уровни атома в отсутствие магнитного поля.

Частота спектральной линии в отсутствии магнитного поля:

Расщепление спектральной линии в магнитном поле.  зависит от магнитного квантового числа, множителя Ланде и магнитной индукции поля. Если g_l = g₂ = g, то

Согласно правилам отбора для магнитного квантового числа, имеем:

Это соответствует трем возможным частотам: ₀ + g_БB/h, 0, ₀  g_БB/h, т. е. в магнитном поле спектральная линия расщепляется и превращается в триплет. Такое расщепление называется нормальным или простым эффектом Зеемана. Он наблюдается в сильных магнитных полях или при g₁ = g₂.

В слабых магнитных полях или при g₁  g₂ существует аномальный эффект Зеемана, и расщепление спектральных линий значительно более сложное.