Уравнение Шредингера. Волновая функция и ее статистический смысл.

Д ля описания движущихся микрочастиц в квантовой теории разработан некий математический формализм, суть которого в следующем. Каждой микрочастице ставится в соответствие некоторая функция, значение которой зависит от координат и времени – это так называемая пси-функция. Формально пси-функция обладает своством классической волны, поэтому её часто называют волновой функцией. Волновая функция является основным носителем информации о волновых и квантовых свойствах частицы и полностью описывает их состояние.

Квадрат модуля волновой функции пропорционален вероятности обнаружить частицу в момент времени t в элементе объёма dV = dx*dy*dz:

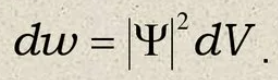
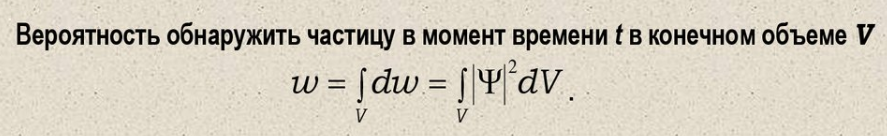
Волновая функция удовлетворяет условию нормировки:

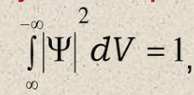
т.е. обнаружить частицу в бесконечном объёме есть достоверное событие.

Согласно опытным данным, параллельный пучок микрочастиц обладает свойствами плоской волны, распространяющейся в направлении движения частиц со скоростью V. Уравнение плоской волны в общем виде:

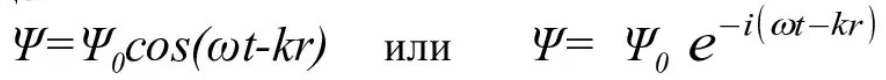
Чтобы это уравнение описывало процесс распространения волн де Бройля (движение микрочастиц), необходимо ввести в него характеристики частицы:

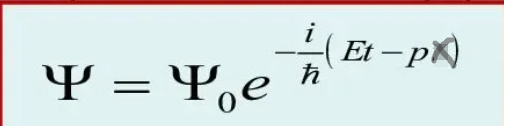r = x

Основным уравнением квантовой механики является уравнение Шредингера. Состояние микрочастиц в квантовой механике описывается волновой функцией или Ψ (пси)-функцией. Эта функция является функцией координат и времени и может быть найдена путем решения уравнения ((общее нестационарное уравнение Шредингера):

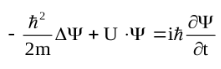
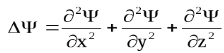
Уравнение Шредингера, как и уравнение Ньютона в классической механике, не может быть получено теоретически, а представляет собой обобщение большого числа опытных фактов. Справедливость этого соотношения доказывается тем, что все вытекающие из него следствия самым точным образом согласуются с опытными фактами.

Из уравнения Шредингера следует, что вид волновой функции Ψ определяется потенциальной энергией U, т.е. характером тех сил, которые действуют на частицу. В общем виде потенциальная энергия U есть функция координат и времени. Для стационарного (не меняющегося во времени) силового поля потенциальная энергия U явно от времени не зависит. В этом случае волновая функция Ψ распадается на два множителя, один из которых зависит только от времени, второй – только от координат.

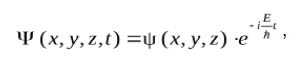
Подставляя эту функцию в уравнение Шредингера, получим:

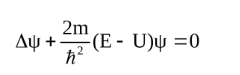
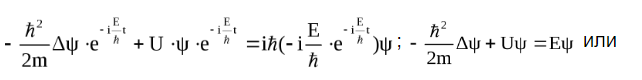
Это уравнение Шредингера для стационарных состояний. Оба уравнения справедливы для любой частицы, движущейся с малой (V«c) скоростью. Кроме того, на волновую функцию накладываются дополнительные условия:

Потенциальный порог (потенциальная ступень). Прохождение частицей потенциального барьера конечной высоты. Туннельный эффект.

Потенциальный порог

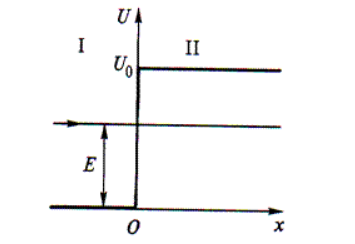
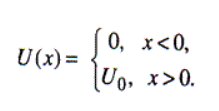
Пусть слева на порог налетает частица с полной энергией Е. На языке квантовой теории это означает, что на порог слева «падает» дебройлевская волна.

Низкий потенциальный порог (E>U₀)

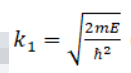
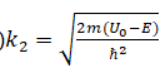
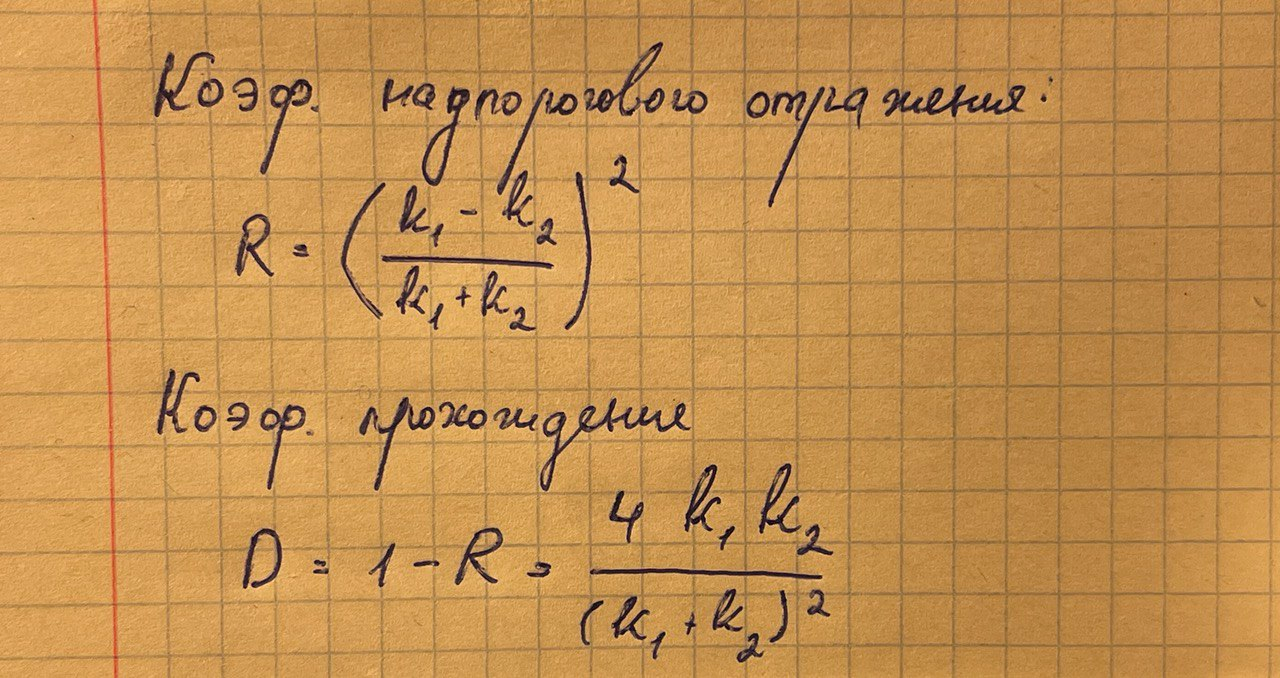
В классическом случае при E>U₀ должно быть R = 0. Эффект надбарьерного отражения(R>0) является чисто квантовым и объясняется наличием у частицы волновых свойств.

Высокий потенциальный порог (E<U₀)

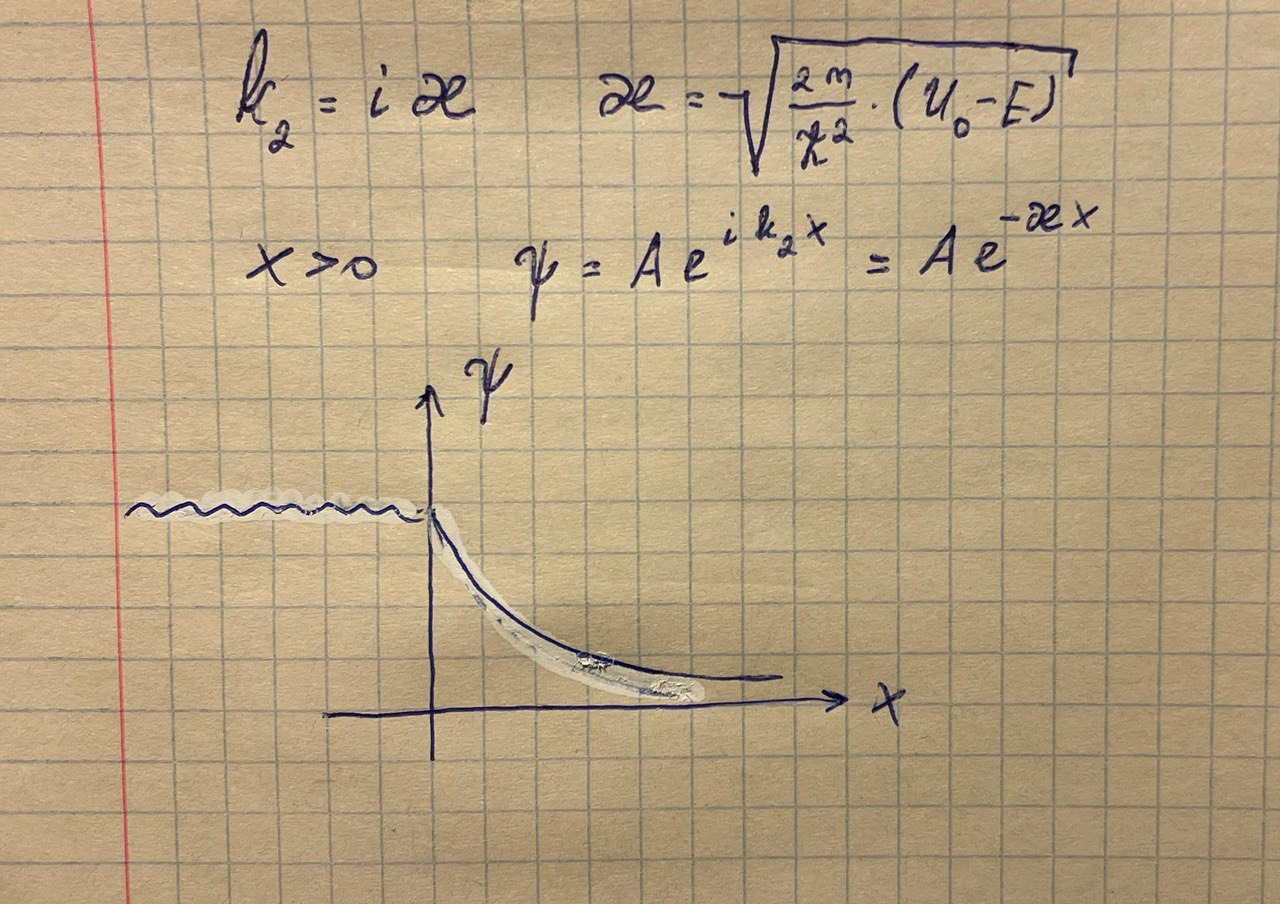
В этом случае хотя и наблюдается явление полного отражения, имеется отличная от нуля вероятность найти частицу в области II, правда, она экспоненциально убывает с уве­личением х. Микрочастица благодаря своим волновым свойствам мо­жет проникать в области, «запрещенные» для классических частиц.

Потенциальный барьер

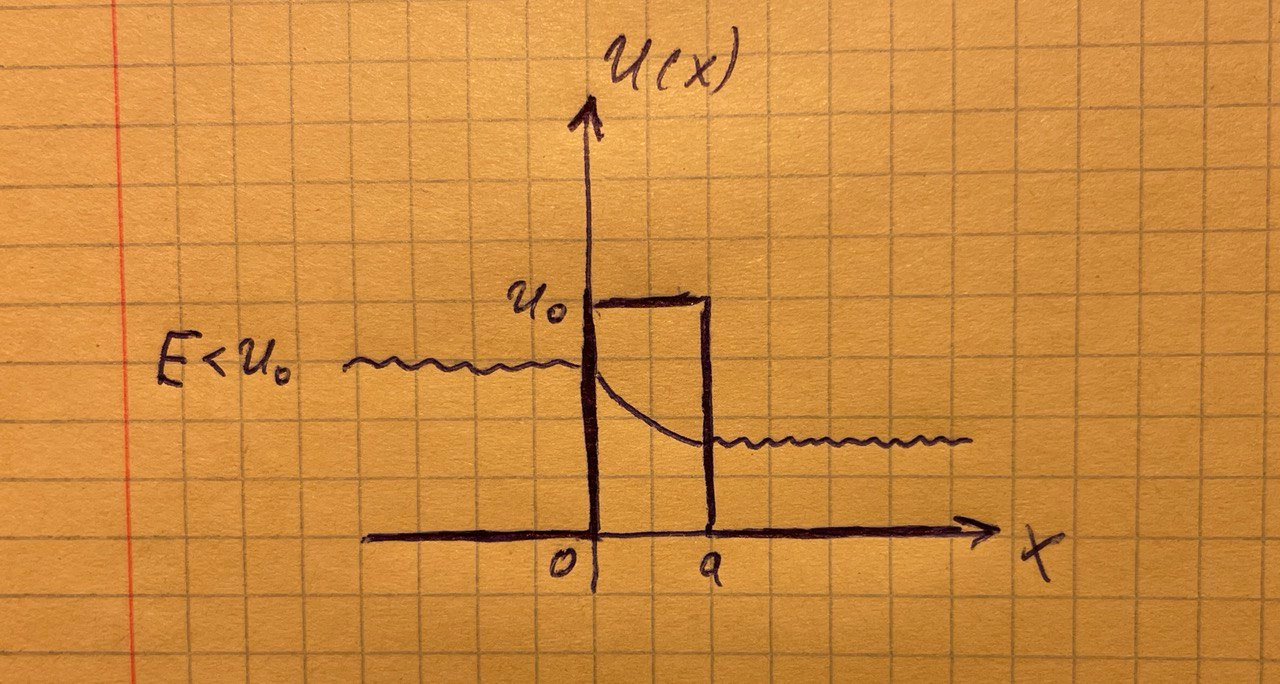
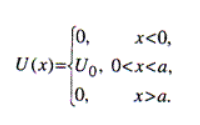
Есть ненулевая вероятность пройти (просачиться) частице через ту область (с уменьшением амплитуды), которую по классическим представлениям она проходить не должна. Это явление называется туннельным эффектом.

Туннельный эффект – явление просачивание частицы через потенциальный барьер.

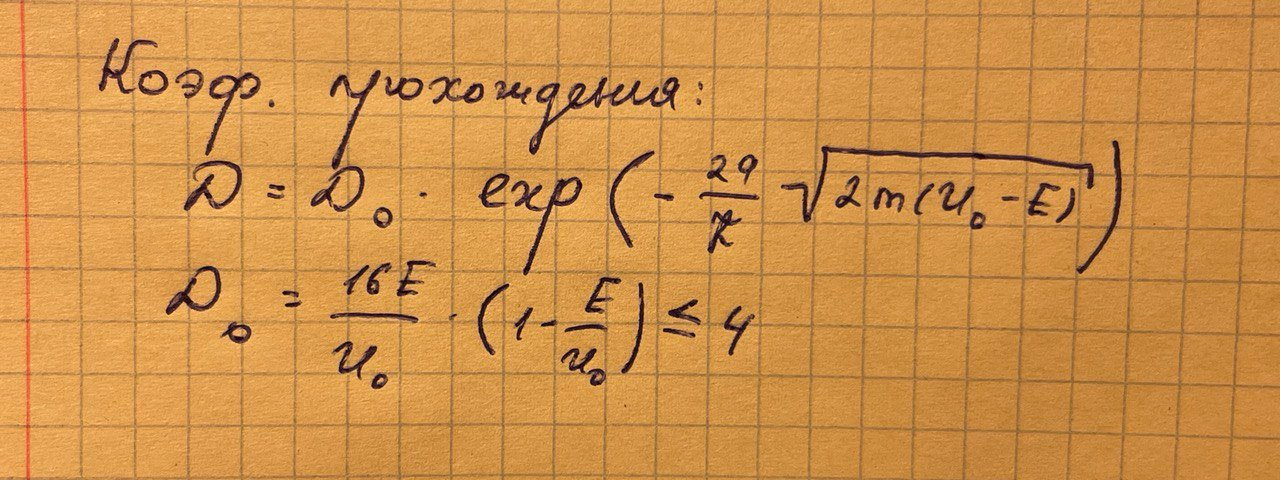
Для потенциального барьера произвольной формы:

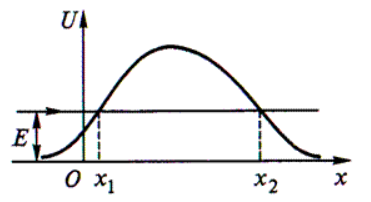
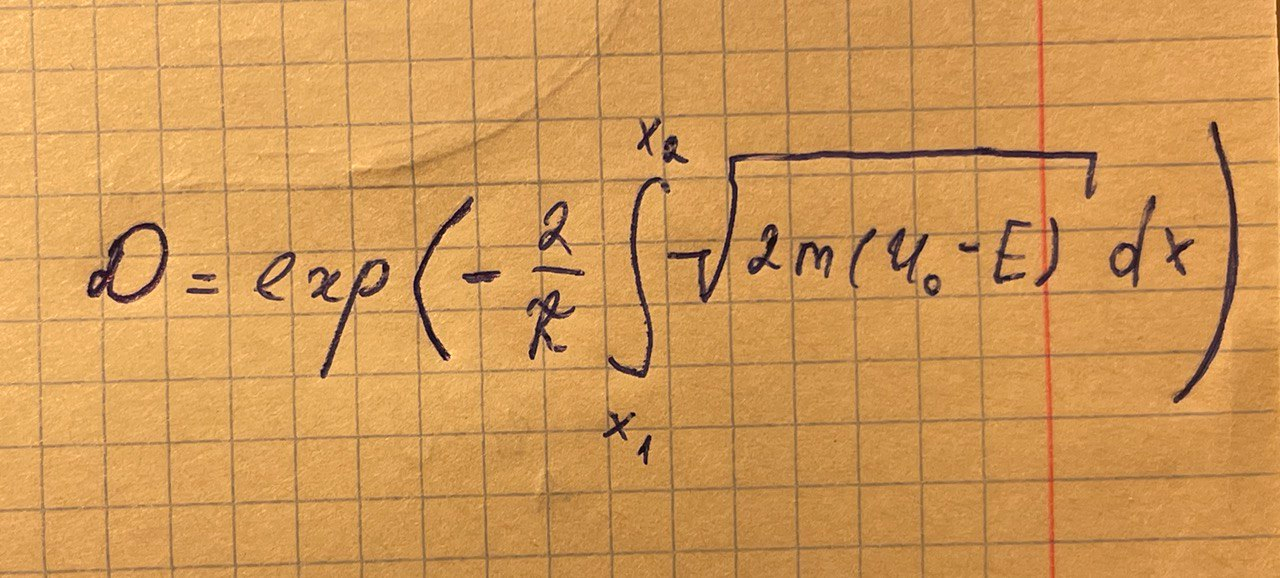
Пределы интегрирования х₁ и х₂ определяют из решения уравнения U(x) = E.