
Проба005
.pdf
Вариант 3. Созинов Максим, группа ПИН-11Д.
Задача 1. |
|
Описать последовательность преобразований графиков |
|
. Функция |
задана на промежутке |
, где
Построить хорошие графики. Один под другим. С обозначением осей координат. Со вспомогательными линиями.
Решение
. Сдвиг вправо по Ох на 1.
. Проведение оси симметрии в х=0 (правую сторону от оси симметрии отражаем зеркально влево).
. Сдвиг вправо по Ох ещё на 2 (т.е. и ось симметрии теперь в х=2). То есть теперь относительно y=cos(x) сдвинуто вправо на три, и в х=2 проведена ось симметрии.
In [1]: import matplotlib.pyplot as plt import numpy as np
x = np.linspace(-2 * np.pi, 2 * np.pi, 1000)
def goPlt(a,b,d,ris): plt.figure(figsize=(10,4)) plt.axhline(y=0, color='k') plt.axvline(x=0, color='k') plt.plot(x, np.cos(a), b, label=d) plt.legend() plt.axis([-7,7,-1.25,1.25]) plt.minorticks_on()
plt.grid(which='major',color = 'k',linewidth = 0.3) plt.grid(which='minor', color = 'k',linewidth = 0.2,linestyle = ':') plt.xlabel('x')
plt.ylabel('y')
plt.title('(рис.{0}) График функции '.format(ris)+d) plt.show()
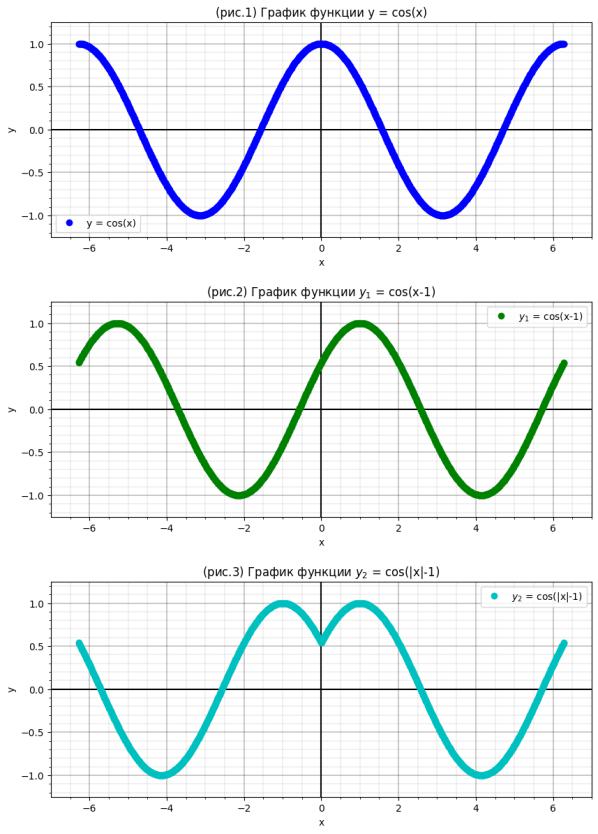
goPlt(x, 'bo', 'y = cos(x)',1) goPlt(x-1, 'go', '$y_1$ = cos(x-1)',2)
goPlt(np.abs(x)-1, 'co', '$y_2$ = cos(|x|-1)',3) goPlt(np.abs(x-2)-1, 'mo', '$y_3$ = cos(|x-2|-1)',4)
In [2]: import matplotlib.pyplot as plt import numpy as np
x = np.linspace(-2*np.pi, 2*np.pi, 200) y = np.cos(x)
y1 = np.cos(x - 1)
y2 = np.cos(np.abs(x) - 1)
y3 = np.cos(np.abs(x - 2) - 1) plt.figure(figsize=(12,5))
plt.plot(x, y, 'b', label='$y = cos(x)$') plt.plot(x, y1, 'go', label='$y_1 = cos(x-1)$') plt.plot(x, y2, 'c', label='$y_2 = cos(|x|-1)$') plt.plot(x, y3, 'm', label='$y_3 = cos(|x-2|-1)$') plt.xlabel('X')
plt.ylabel("Y") plt.legend(facecolor = 'oldlace') plt.axhline(y=0, color='k') plt.axvline(x=0, color='k')
plt.axvline(x=2, linestyle='--',color='0.6')
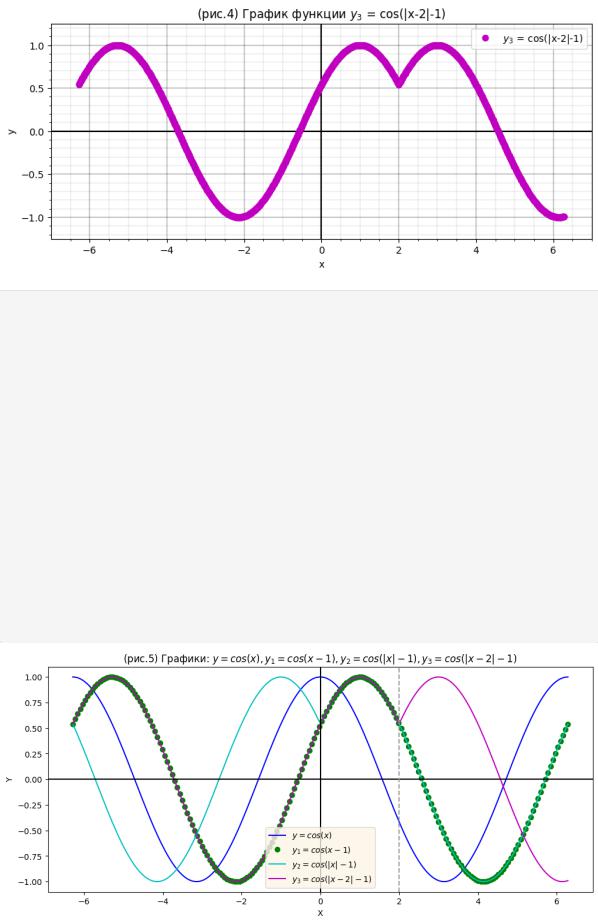
plt.title('(рис.5) Графики: $y = cos{(x)}, y_1=cos{(x - 1)}, y_2=cos{(|x| - 1)}, y_ plt.show()
Так же из рисунка "5" видно: |
на промежутке |
на |

промежутке |
на промежутке |
. |
|
|
|
|
|
|
Задача 2.
Найти приближённые и точные значения в алгебраической форме корней сначала письменно, используя формулу Муавра для извлечения корней.
Что такое модуль комплексного числа. Что такое главный аргумент комплексного числа? В каких пределах он задается? Используя операции отношения для приближённых значений корней выяснить какие корни лежат на мнимой оси, какие корни имеют главный аргумент равный . Сделать
три рисунка, дать им описание (что мы на них видим и почему)
1)На первом рисунке изобразить комплексную плоскость, окружность и все найденные корни.
2)На втором рисунке изобразить комплексную плоскость, отметить окружность и только те корни., которые лежат на мнимой оси.
3)На третьем рисунке отметить корни, главный аргумент которых равен |
. |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Комплексное число |
|
|
|
|
|
|
|
, модуль комплексного числа - это длина его |
|
||||||||||
радиус-вектора. |
|
|
|
|
|
. |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|||||||||||||
Тригонометрическая запись комплексного числа |
, |
|
|||||||||||||||||
где главный аргумен комплексного числа. Это угол, образуемый между радиус- |
|
||||||||||||||||||
вектором и положительной полуоси действительной части комплексного числа. |
|
||||||||||||||||||
|
|
|
|
|
. Задаётся в пределах: |
. |
|
||||||||||||
|
|
|
|
|
|
||||||||||||||
По формуле Муавра |
|
|
|
- имеет n корней ( |
). |
|
|||||||||||||
|
|
|
|
||||||||||||||||
Корни |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
(остальные целые будут лишь повторять эти корни). |
|
|
|||||||||||||||||
Представим наше число |
|
|
в тригонометрической форме: |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
. |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
Запишем формулу корней в общем виде:
Подставим
Подставим
-(корень с главным аргументом
)
Подставим

т к |
то вычтем |
-(т.к. действительная часть равна нулю, значит лежит на мнимой оси)
In [3]: import matplotlib.pyplot as plt import numpy as np
import sympy as sp
def znk(b, a): print(b,'значения:')
z = ['z\u2080','z\u2081','z\u2082'] for i in range(3):
print(z[i],' = ',end='') sp.pprint(a[i])
print()
def goPlt(Zn,ris): plt.axhline(y=0, color='k') plt.axvline(x=0, color='k')
t = np.linspace(0,2*np.pi,100) plt.plot(r**(1/3)*np.cos(t),r**(1/3)*np.sin(t),':') nol = np.zeros(3)
plt.quiver(nol, nol, np.real(Zn), np.imag(Zn),angles='xy', scale_units='xy', sc plt.scatter(np.real(Zn),np.imag(Zn), marker="*", color="red", s=200) plt.xlabel('Re(z)')
plt.ylabel('Im(z)') plt.axis('equal') plt.grid(True) plt.title(ris) plt.show()
z = 27j
r = np.abs(z)
phi = np.angle(z) k = np.arange(0,3)
Zn = r**(1/3)*(np.cos((phi+2*np.pi*k)/3)+1j*np.sin((phi+2*np.pi*k)/3))
znk('Приближённые', np.round(Zn,2))
Zk = [0,0,0]
for i in range(3):
Zk[i] = r**(1/3)*(sp.cos((sp.pi/2+2*sp.pi*i)/3)+1j*sp.sin((sp.pi/2+2*sp.pi*i)/3
znk('Точные',Zk)
L1 = np.isclose(np.real(Zn),0) print(np.round(Zn[L1],2),' - лежит на мнимой оси')
L2 = np.isclose(np.angle(Zn),5*np.pi/6) print(np.round(Zn[L2],2),' - имеет главный аргумент 5\u03C0/6')
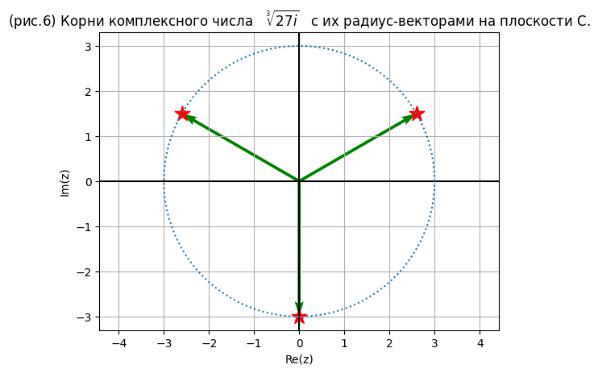
goPlt(Zn,'(рис.6) Корни комплексного числа $\sqrt[3]{27i}$ с их радиус-векторам
goPlt(Zn[L1],'(рис.7) |
Корень |
комплексного |
числа |
$\sqrt[3]{27i}$, |
который |
лежит |
на |
goPlt(Zn[L2],'(рис.8) |
Корень |
комплексного |
числа |
$\sqrt[3]{27i}$, |
который |
имеет |
гл |
|
|
|
|
|
|
|
|
Приближённые значения: z = (2.6+1.5j)
z = (-2.6+1.5j) z = (-0-3j)
Точные значения: z = 1.5 √3 + 1.5
z = -1.5 √3 + 1.5 z = -3.0
[-0.-3.j] |
- лежит на мнимой |
оси |
[-2.6+1.5j] |
- имеет главный |
аргумент 5π/6 |
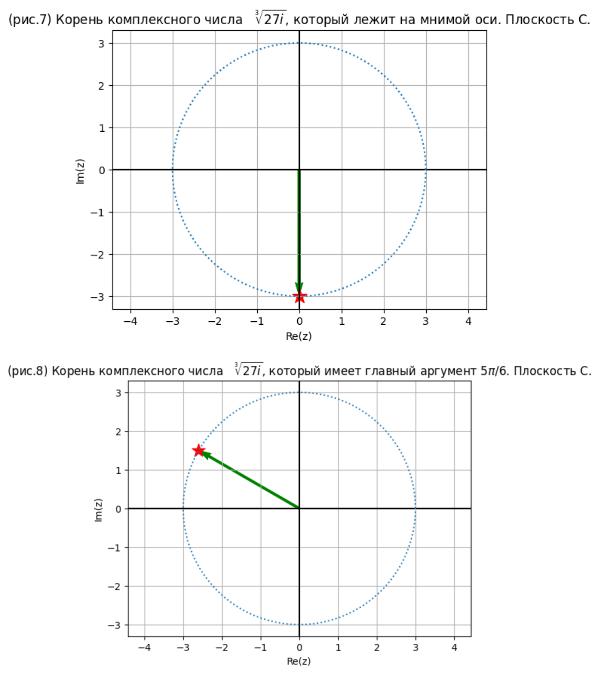
Красными звёздочками ( ) на рисунках 6,7,8 отмечены комплексные числа на комплексной плоскости "C".
Горизонтальная ось (Real или сокращенно Re(z)) - действительная часть комплексного числа. ("действительная ось")
Вертикальная ось (Imag или сокращенно Im(z)) - мнимая часть комплексного числа. ("мнимая ось")
Модуль комплексного числа - это радиус окружности, на которой и расположены комплексные числа.
Зелёными стрелками ( ) на рисунках изображены радиус-векторы комплексных чисел.
По формуле Муавра наши корни |
|
|
|
|
|
|
|
, |
|
|
||
|
|
|
|
|
|
|||||||
где |
|
- начальный угол, откладываемый от положительной части |
|
|
|
|||||||
|
|
|
|
|||||||||
"действительной оси" до радиус-вектора первого корня комплексного числа |
|
; |
||||||||||
|
||||||||||||

а- это угол между радиус-векторами корней нашего комплексного числа
.
Соответственно, построение можно делать как с помощью этих углов и модуля комплексного числа, так и по координатам действительной и мнимой частей комплексного числа.
Ну и соответственно, если комплексное число лежит на мнимой оси, значит действительная часть равна нулю; если на действительной оси, значит мнимая часть
равна нулю. |
|
У корня " |
Re(z)>0 и Im(z)>0, поэтому он в первой четверти. |
У корня " |
Re(z)<0 и Im(z)>0, поэтому он во второй четверти. |
У корня " |
Re(z)=0 и Im(z)<0, поэтому он на мнимой оси с нижней |
стороны. |
|
|
|
|
|
Задача 3.
Построить графики функций |
.Решить неравенства |
, получить |
|
точные и приближённые ответы так, как этому учили в лабораторных |
|||
практикумах: |
б |
|
|
a) |
. |
|
|
В отчёт вставить графики, точный и приближённый ответы в виде промежутков, объяснить результаты.
Решение . a)
In [4]: import matplotlib.pyplot as plt import numpy as np
x= np.linspace(-5, 11, 100) plt.figure(figsize=(10,5)) plt.plot(x, x**3-10*x**2-2 ,'b') plt.axhline(y=0, color='k') plt.axvline(x=0, color='k') plt.axis([-5,11,-155,30]) plt.xlabel('x')
plt.ylabel('y') plt.grid(True)
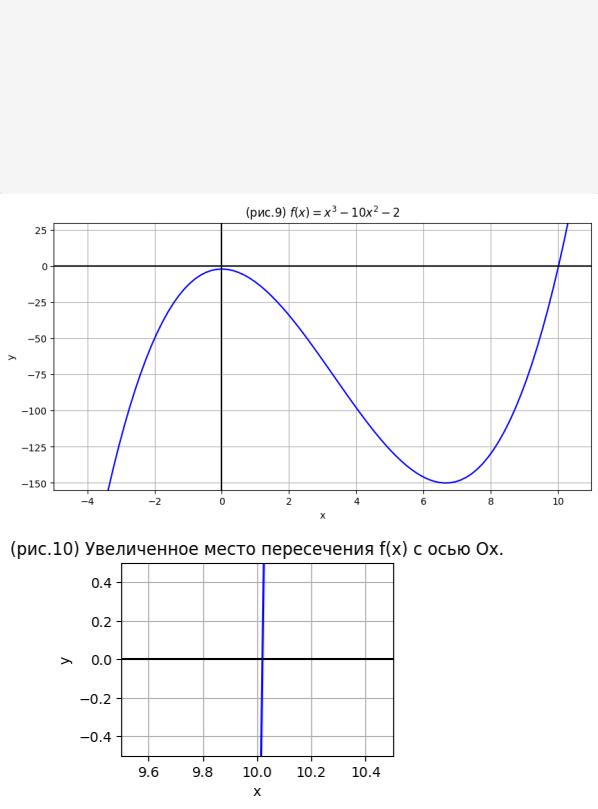
plt.title('(рис.9) $f(x)=x^3-10x^2-2$') plt.show()
x= np.linspace(9.5, 10.5, 50)
plt.figure(figsize=(3.5,2.5)) plt.plot(x, x**3-10*x**2-2 ,'b') plt.axhline(y=0, color='k') plt.axvline(x=0, color='k') plt.axis([9.5,10.5,-0.5,0.5])
plt.xlabel('x') plt.ylabel('y') plt.grid(True)
plt.title('(рис.10) Увеличенное место пересечения f(x) с осью Ox.') plt.show()
import sympy as sp
from sympy.abc import x
a = sp.solve_univariate_inequality(x**3 - 10*x**2>=2,x,relational=False) sp.pprint(a)
sp.N(a,4)
|
|
|
|
|
|
______________ |
|
|
|
|
100 |
10 |
|
√6081 |
1027 |
||
──────────────────── + ── + 3 |
───── + ──── , ∞ |
|||||||
|
|
|
______________ 3 |
|
9 |
27 |
|
|
|
|
|
√6081 |
1027 |
|
|
|
|
9 |
|
3 |
───── + ──── |
|
|
|
|
|
|
|
9 |
27 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
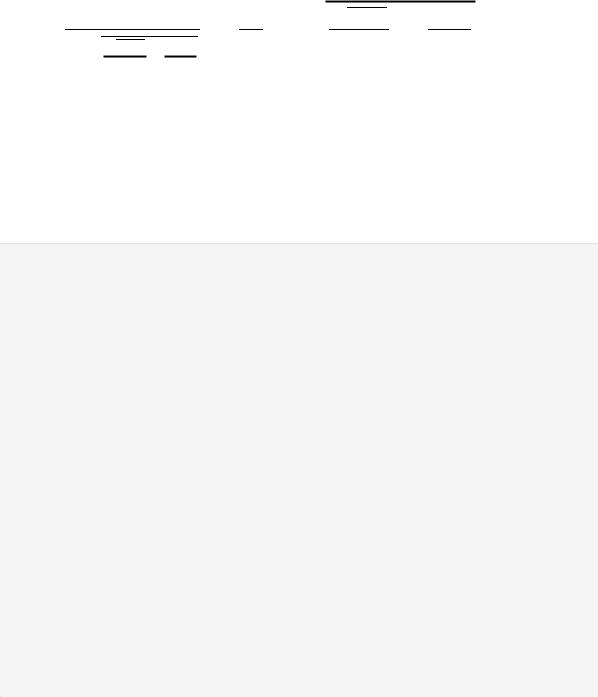
Out[4]:
-
точное значение.
- приближённое значение (до 2 знаков
после запятой).
б
In [5]: import matplotlib.pyplot as plt import numpy as np
x = np.linspace(-5, 11, 100) plt.figure(figsize=(10,5)) plt.plot(x, x**3-10*x**2+15 ,'g') plt.axhline(y=0, color='k') plt.axvline(x=0, color='k') plt.axis([-5,11,-140,30]) plt.xlabel('x')
plt.ylabel('y') plt.grid(True)
plt.title('(рис.11) $f(x)=x^3-10x^2+15$') plt.show()
import sympy as sp x = sp.symbols('x')
Xn = sp.solve('x**3-10*x**2+15', x) print('(Точное значение) x\u2081 =') sp.pprint(Xn[1])
print('----\n\n(Точное значение) x\u2082 =') sp.pprint(Xn[0])
print('----\n\n(Точное значение) x\u2083 =') sp.pprint(Xn[2])
a = sp.solve_univariate_inequality(x**3 - 10*x**2>=-15.0,x,relational=False) sp.N(a,3)
