3. Аналитические вычисления

Задание 1: Определить точку пересечения двух прямых, описываемых уравнениями

х + 2∙π∙у = а

4∙х + у = b

3.1.1. Запустите программу MathCad.

3.1.2. Введите ключевое слово given.

3.1.3. Введите уравнения прямых.

3.1.4. Введите функцию find, перечислив в качестве параметров неизвестные х, у. Затем введите оператор аналитического вычисления комбинацией клавиш CTRL и . или ввести команду Вычислить, Вычислить в символах из меню ″Символика″.

3.1.5. Щелкните за пределами данного блока, и программа MathCad произведет анали­тическое решение системы уравнений.

Задание 2: Найти все корни уравнения:

(1 + y – y²)² +y = 2

Это уравнение четвертого порядка. Легко подобрать один корень (у = 1). Остающееся уравнение третьего порядка не имеет рациональных корней, так что поиск других корней этого уравнения – дело непростое. Неясно даже, сколько еще действительных корней имеет данное уравнение. Результаты численного решения зависят от подбора начального приближения и поэтому не гарантируют отыскание всех корней уравнения. Мы же решим это уравнение аналитически.

3.2.1. Введите заданное уравнение. Чтобы раскрыть скобки, в начале выделите все выражение, а затем дайте команду Symbolics → Simplify (Аналитические вычисления → Упростить).

3.2.2. Выделите в полученном уравнении независимую переменную (в данном слу­чае у) и выберите Решить относительно переменной из меню ″Символика″.

Программа MathCad выдаст вектор, элементами которого являются корни дан­ного уравнения.

3.2.3. Для упрощения полученного выражения вначале выделите его, а затем дайте команду Symbolics → Simplify (Аналитические вычисления → Упростить).

3.2.4. Чтобы получить результат в числовом виде (1, 1.802, -1.247, 0.445), достаточно ввести в конце выраже­ния (итогового или на любой из предыдущих стадий) команду вычисления (=).

Задание 3: Вычислить интеграл от х²∙е^х в общем виде.

3.3.1. Запустите программу MathCad.

3.3.2. Введите заданную функцию.

3.3.3. Щелкните на х (после этого она будет выделена в виде черного прямоугольника).

3.3.4. Выберите команду Интегрировать по переменной из меню ″Символика″.

3.3.5 Или

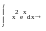
Содержание отчета: 1) задание на работу; 2) исходные данные, математические формулы и результаты расчетов; 3) выводы по работе.

4. Решение дифференциальных уравнений

З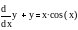 адание: Найти функцию у(х), удовлетворяющую дифференциальному уравнению

и имеющую значение 0 при x = 0.

Это простое дифференциальное уравнение допускает точное аналитическое решение, однако в данном упражнении предполагается использование стандартной функции программы MathCad, осуществляющей численное решение данного урав­нения. Результат вычислений можно после этого сравнить с точным решением.

4.1. Запустите программу MathCad.

4.2. Задайте начальное значение функции как элемент вектора у, размерность которого соответствует числу решаемых уравнений: у₀:= 0.

4.3. Создайте функцию Т(х, у), которая вычисляет значение производной при задан­ных значениях независимой переменной и неизвестной функции:

T(x, y) := –y₀ + x∙cos(x).

4.4. Определите начальное (точка 0) и конечное значение отрезка интегрирования. a :=0, b := 12∙.

4.5. Укажите число шагов интегрирования К:=20.

4.6. Вычислите численное решение уравнения при помощи функции rkfixed.

Z:= rkfixed(y,a,b,K,T).

Результат вычислений – матрица Z с двумя столбцами, первый из которых содержит значения независимой переменной, а второй — соответствующие зна­чения функции.

4.7. Постройте график полученного решения.

4.8. Измените число шагов, на которые делится отрезок интегрирования, и иссле­дуйте, как изменяется результат расчета при уменьшении и увеличении этого параметра.

Содержание отчета: 1) задание на работу; 2) исходные данные, математические формулы и результаты расчетов; 3) графики; 4) выводы по работе.