
X
- •ТЕОРИЯ
- •Лекция 2
- •Двухстороннее преобразование Фурье
- •Обратное преобразование Фурье
- •Фурье. Теорема линейности
- •дифференцирования
- •Теорема интегрирования оригинала
- •Теорема
- •масштабирования
- •Молния
- •Franklin
- •Трагическая гибель
- •Релея
- •Вывод
- •Пример
- •Найдем спектральную плотность F(j )
- •Вывод
- •ФЧХ ( ) arctg ( )
- •передачи сигналов через ЭЦ
- •f1(t) – входной сигнал, f2(t) – выходной сигнал
- •Математическое условие
- •Неискажающая
- •спектральным
- •Спектральную плотность входного сигнала
- •Спектральную плотность выходного сигнала
- •Найдем передаточную функцию такой цепи
- •Акустическая система
- •акустической системы
- •АЧХ акустической
- •Идеальные АЧХ колонок с сабвуфером
- •Реальные АЧХ колонок с сабвуфером
- •искажений
- •плотности токов и
- •спектров
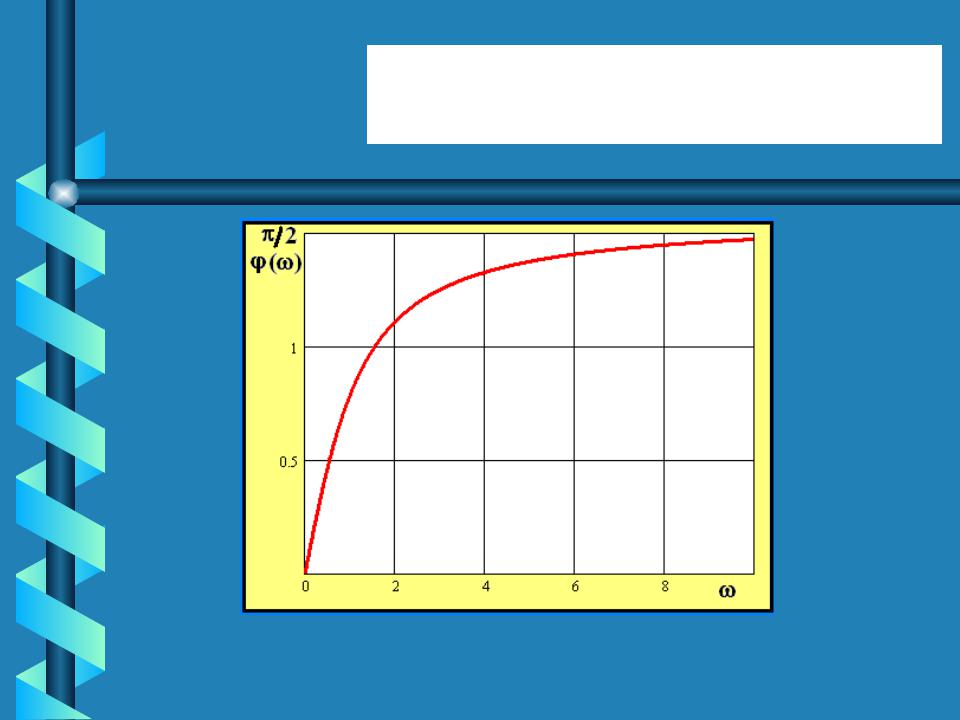
 ФЧХ ( ) arctg ( )
ФЧХ ( ) arctg ( )
21

передачи сигналов  через ЭЦ
через ЭЦ
•Рассмотрим условия, которым должны удовлетворять частотные характеристики цепи, чтобы сигнал, проходил через цепь без искажения своей формы
22
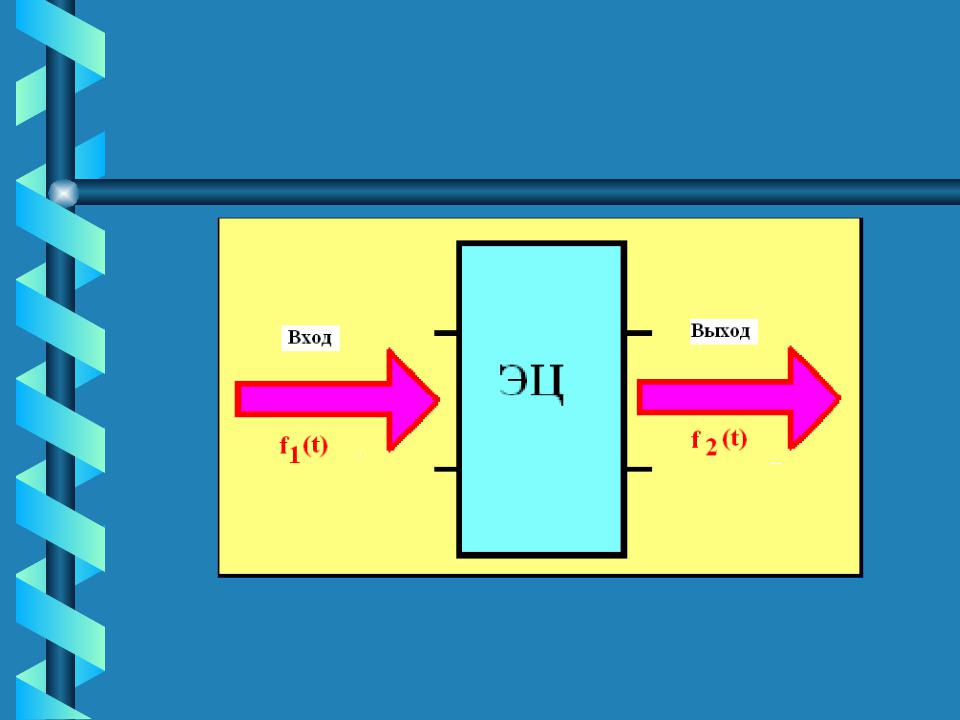
f1(t) – входной сигнал,  f2(t) – выходной сигнал
f2(t) – выходной сигнал
23

Математическое условие
 неискаженной передачи
неискаженной передачи
f2 (t) k f1 (t t0 ),
 • k – постоянный множитель;
• k – постоянный множитель;
• t0 – время запаздывания. 24

Неискажающая
 цепь
цепь
 • Если форма сигнала сохраняется неизменной, то передача сигнала называется неискаженной, а сама цепь называется
• Если форма сигнала сохраняется неизменной, то передача сигнала называется неискаженной, а сама цепь называется
неискажающей. 25
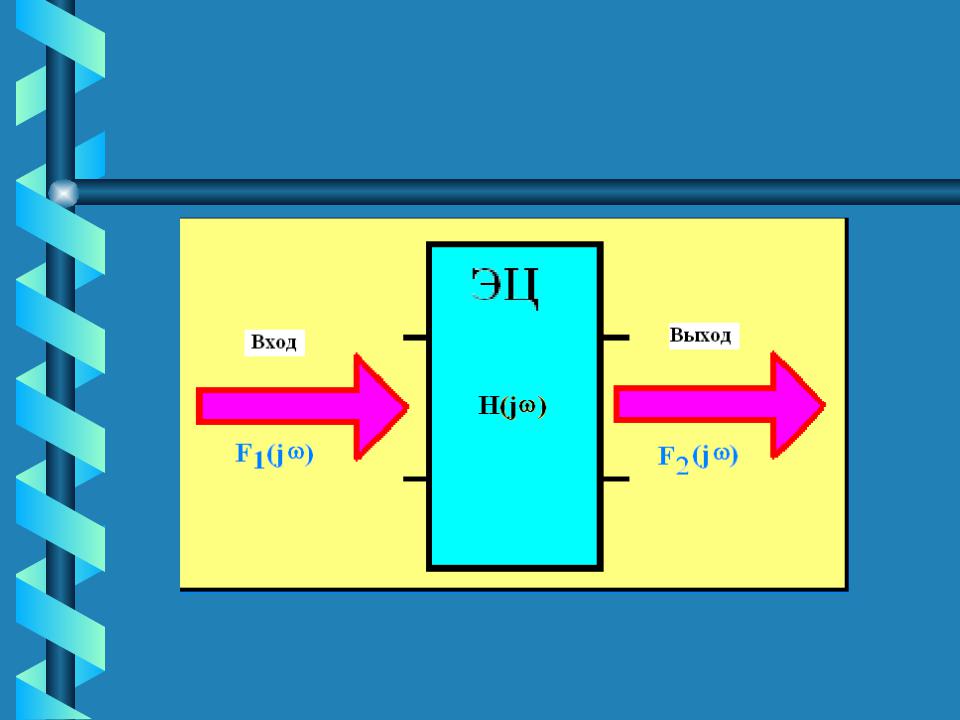
спектральным
 плотностям
плотностям
26

Спектральную плотность  входного сигнала
входного сигнала
F1 ( j ) f1 (t)e j t dt,
27

Спектральную плотность  выходного сигнала
выходного сигнала
28

Найдем передаточную  функцию такой цепи
функцию такой цепи
H H ( j ) F2 ( j ) k F1 ( j ) e j t0 F1 ( j ) F1 ( j )
k e j t0 H ( )e j ( ) ,
H ( ) k,
 ( ) t0 .
( ) t0 .
29
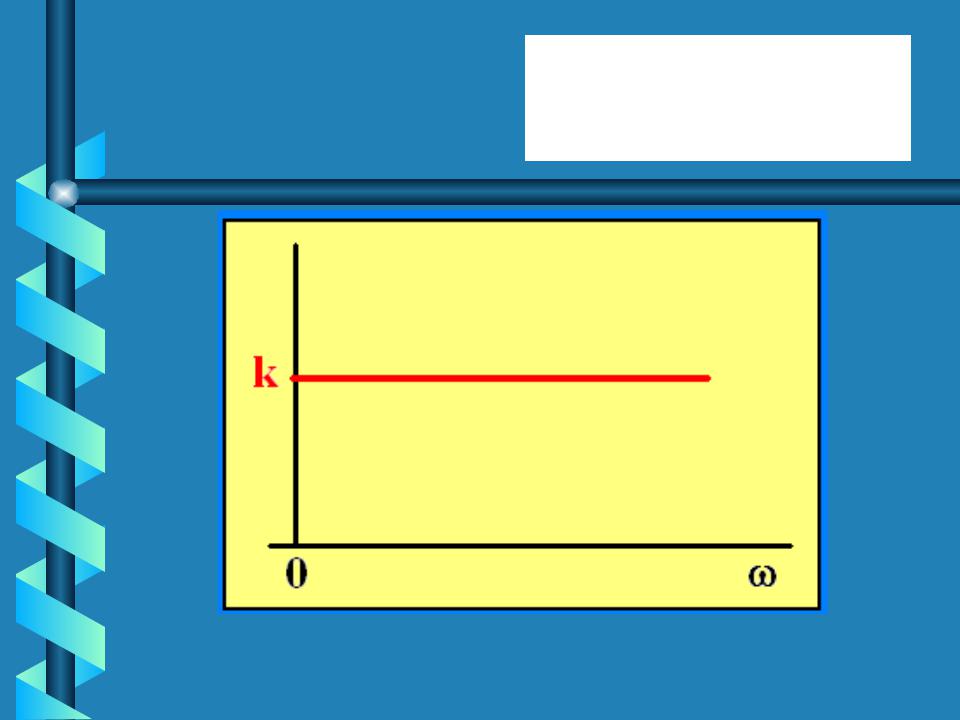
 АЧХ H ( ) k
АЧХ H ( ) k
30
Х |
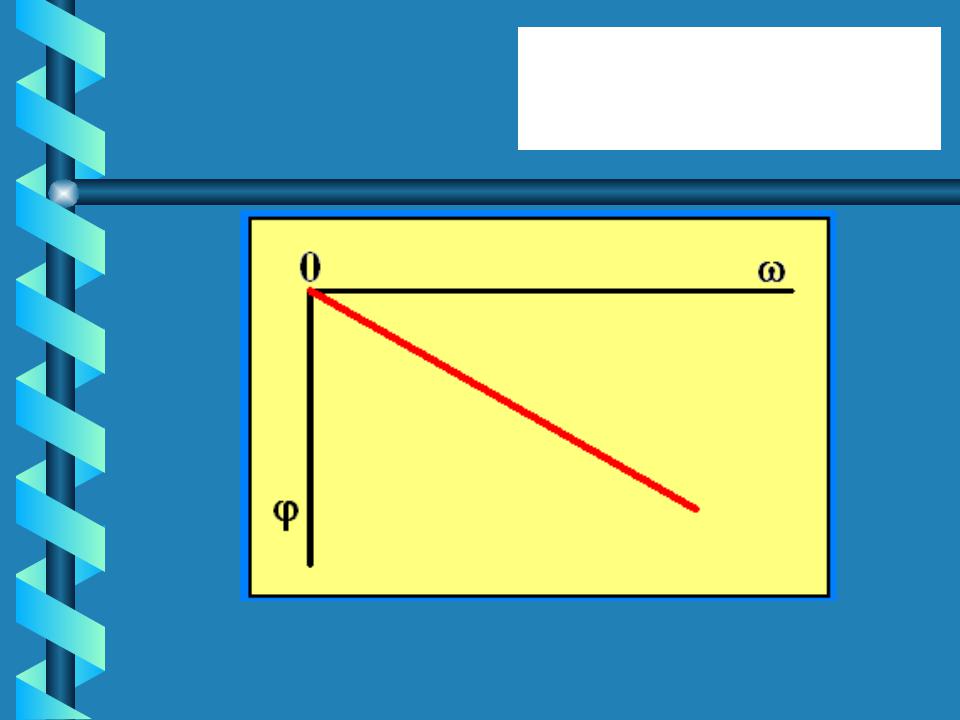
( ) t0 |
|
31
Соседние файлы в папке Лекции
