А) коагуляционно – тиксотропные; Б) конденсационно-кристаллизационные;
В) обратимые дилатантные (жидкокристаллические). 7. Коагуляционные структуры образуются:
А) в лиофобных дисперсных системах, если концентрация частиц Б) в лиофобных дисперсных системах, если концентрация частиц
дисперсной фазы мала, а частицы коагулируют во втором потенциальном минимуме;
В) если между частицами возникают атомные контакты и по всему объёму системы образуется пространственная сетка;
Г) если в системе возникает пространственная сетка в результате взаимофиксации частиц во втором потенциальном минимуме.
8. В дисперсных системах конденсационные структуры образуются при: А) коагуляции частиц во втором потенциальном минимуме; Б) образовании пространственной сетки в результате взаимофик-
сации частиц через прослойки дисперсионной среды; В) возникновении пространственной сетки в результате непосред-
ственных контактов между частицами и образования химических связей.
8.2.Моделирование реологических свойств
1.Реологическая модель вязкопластичного тела Бингама состоит из идеальных моделей:
|
А) одной; |
Б) двух; |
В) трёх; |
Г) четырёх. |
2. |
Реологическая модель вязкоупругого тела Кельвина-Фойгта состоит из |
|||
идеальных моделей: |
|
|
|
|
|
А) одной; |
Б) двух; |
В) трёх; |
Г) четырёх. |
3. |
Реологические свойства каких тел описывает модель Бингама: |
|||
|
А) вязких; |
Б) упругих; |
В) пластических; |
|
|
Г) вязкопластических. |
|
|
|
4. |
Реологические свойства каких тел описывает модель Кельвина-Фойгта: |
|||
|
А) вязких; |
Б) упругих; |
В) вязкоупругих; |
|
109
Г) пластических Д) вязкопластических.
5.Реологические свойства каких тел описывает модель Сен-Венана– Кулона:
А) вязких; Б) упругих;
В) пластических; Г) вязкопластичных.
6.Идеально упругое тело моделируется:
А) идеально упругой пружиной; Б) движением перфорированного поршня в цилиндре, заполнен-
ном идеально вязкой жидкостью; В) твёрдым телом, скользящим по поверхности.
7. Идеально вязкое тело моделируется: А) идеально упругой пружиной;
Б) движением перфорированного поршня в цилиндре, заполненном идеально вязкой жидкостью;
В) твёрдым телом, скользящим по поверхности. 8. Идеально пластическое тело моделируется:
А) идеально упругой пружиной; Б) движением перфорированного поршня в цилиндре, заполнен-
ном идеально вязкой жидкостью; В) твёрдым телом, скользящим по поверхности.
9. Элементарными (идеальными) реологическими моделями являются модели:
А) Гука; |
Б) Бингама; |
В) Сен-Венана-Кулона; |
В) Максвелла; |
Г) Кельвина-Фойгта; |
Д) Ньютона. |
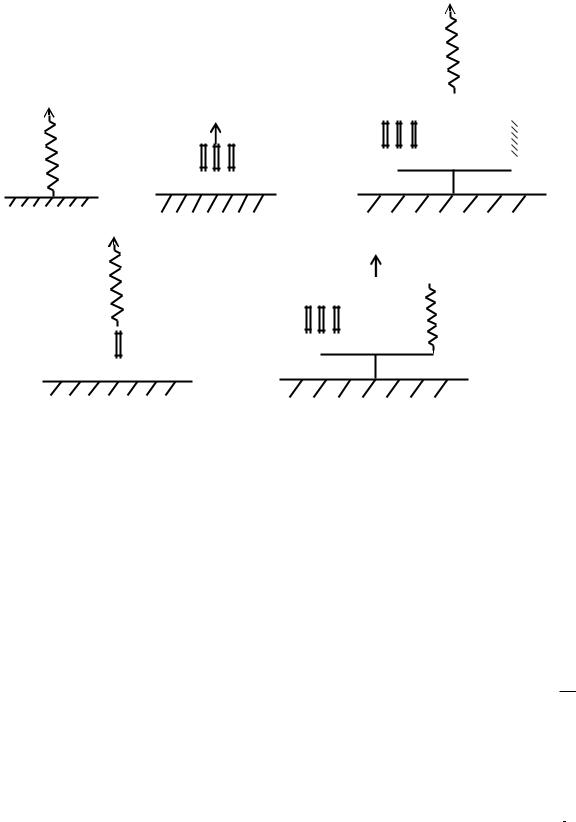
10. Установите соответствие между названиями реологических моделей и их схематическим представлением:
1)идеально вязкое тело Ньютона;
2)упруговязкое тело Максвелла;
3)идеально упругое тело Гука;
4)вязкопластичное тело Бингама;
5)вязкоупругое тело Кельвина-Фойгта.
110
А) |
Б) |
|
|
В) |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Г) |
|
|
Д) |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11. Установите соответствие между реологическими параметрами и еди-
ницами их измерения: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1) деформация; |
2) напряжение сдвига; |
|
|
|
|
3) вязкость; |
|
|
||||||
4) скорость деформации. |
|
|
|
|
|
|
|
|
|
|
|
|||
А) Па.с; |
Б) Па; |
|
В) безразмерная величина; |
|
Г) с–1 |
|||||||||
12. Закон Ньютона выражается уравнением: |
|
|
|
|
|
|
|
|
|
|
||||
|
|
dy |
|
|
dy |
n |
|
– |
т |
|
||||
А) P = Ey ; |
Б) P = 1 |
; |
В) P k |
|
; |
Г) |
л |
, |
||||||
|
|
|
|
P = P е |
||||||||||
|
|
|||||||||||||
|
|
dт |
|
|
|
|
|
|
0 |
|
|
|||
|
|
|
|
dт |
|
|
|
|
|
|||||
где Р – механическое напряжение, Р0 – начальное механическое напряже-
ние, Е – модуль Юнга, y – деформация, 1 – динамическая вязкость, dy – dт
скорость деформации.
13. Поведение вязкопластичных тел Бингама (кривую течения) описывает уравнение:
|
|
|
|
|
|
|
|
n |
|
|
|
А) P = Ey ; |
Б) P = 1 |
dy |
; |
|
В) P k |
|
dy |
|
; |
Г) P P + 1* dy , |
|
|
|
||||||||||
|
|
dт |
|
|
|
|
|
T |
dт |
||
|
|
|
dт |
|
|
||||||
где Р – механическое напряжение, Е – модуль Юнга, |
y – деформация, 1 – |
||||||||||
вязкость, 1* – пластическая вязкость; |
dy |
– скорость деформации, РT – пре- |
|||||||||
|
|||||||||||
dт
дел текучести.
111
14. Закон Гука описывается уравнением: |
|
|
dy n |
|
|
|
|
|||||||||
|
|
dy |
|
|
|
|
|
|
Г) P P + 1* |
dy |
||||||
А) P = Ey ; |
Б) P = 1 |
|
; |
|
|
В) |
P k |
|
|
|
|
; |
|
, |
||
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|||
|
|
dт |
|
|
|
|
|
dт |
|
|
dт |
|||||
где Р – механическое напряжение, Е – модуль Юнга, |
y – деформация, |
1 – |
||||||||||||||
вязкость, 1* – пластическая вязкость; |
dy |
|
– скорость деформации, РT – пре- |
|||||||||||||
dт |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
дел текучести. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15. Поведение упруговязких тел Максвелла описывается уравнением: |
|
|
||||||||||||||
|
Б) P = 1 |
dy |
; |
|
|
В) |
|
dy n |
|
|
|
|
||||
А) P = Ey ; |
|
|
|
P k |
|
|
; |
|
|
|
||||||
|
|
|
|
|
|
|
||||||||||
|
|
dт |
|
|
|
|
|
dт |
|
|
|
|
||||
|
|
|
|
|
|
dy |
Д) P = P е– |
т |
|
|
|
|
|
|
|
|
|
|||||
Г) P – P |
|
= 1* |
|
|
л , |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
T |
|
|
dт |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где Р – механическое напряжение, Р0 – начальное механическое напряже- |
||||||||||||||||||||||
ние, Е – модуль Юнга, |
y – деформация, 1 – вязкость, 1* – пластическая |
|||||||||||||||||||||
вязкость; |
dy |
– |
|
скорость деформации, |
РT – |
предел текучести, т – время |
||||||||||||||||
|
|
|||||||||||||||||||||
|
dт |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
действия нагрузки, л – время релаксации напряжения. |
|
|
|
|
|
|
|
|||||||||||||||
16. Установите соответствие между реологическими моделями и уравне- |
||||||||||||||||||||||
ниями, описывающими их поведение: |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
1) идеально упругое тело Гука; |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
2) идеально вязкое тело Ньютона; |
|
|
|
|
|
|
|
|
|
|||||||||||||
3) упруговязкое тело Максвелла; |
|
|
|
|
|
|
|
|
|
|||||||||||||
4) вязкоупругое тело Кельвина-Фойгта; |
|
|
|
|
|
|
|
|||||||||||||||
5) вязкопластическое тело Бингама. |
|
|
|
|
|
|
|
|
|
|||||||||||||
А) P = Ey ; |
|
|
|
Б) P = 1 dy |
; |
|
В) y = P0 |
|
|
|
т |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 – exp |
– |
|
; |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
dт |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
E |
|
|
|
0 |
||||||||
|
т |
|
|
|
Д) P P + 1* dy |
|
|
|
|
|
|
|
|
|
||||||||
Г) P = P е – л |
; |
|
|
, |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
0 |
|
|
|
|
T |
|
dт |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где Р – механическое напряжение, Р0 – начальное напряжение, Е – модуль |
||||||||||||||||||||||
Юнга, y – деформация, |
1 – вязкость, |
dy |
– скорость деформации, РT – пре- |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
dт |
||||||||||||
дел текучести, |
т – время действия нагрузки, |
л – время релаксации напря- |
||||||||||||||||||||
жения, 0 – время релаксации деформации. |
|
|
|
|
|
|
|
|
|
|||||||||||||
112
17. Жидкость ведёт себя как твёрдое тело при следующем соотношении между временем приложения напряжения т и временем релаксации
напряжения л : |
|
|
|
А) т = л ; |
Б) т > л ; |
В) т >> л ; |
Г) т << л . |
18. Твёрдое тело ведёт себя как жидкость при следующем соотношении между временем приложения напряжения т и временем релаксации
напряжения л : |
|
|
|
А) т = л ; |
Б) т > л ; |
В) т >> л ; |
Г) т << л . |
19. Время релаксации напряжения л в уравнении реологической модели
– т
упруговязкого тела Максвелла P = P0е л – это время, в течение которого начальное напряжение в теле:
А) остаётся постоянным; Б) уменьшается до нуля; Г) уменьшается в е раз.
20. Время релаксации деформации 0 в уравнении реологической модели
– т
вязкоупругого тела Кельвина-Фойгта y = y0e 0 – это время, в течение которого деформация в теле после снятия нагрузки:
А) остается постоянной; Б) уменьшается до нуля; Г) уменьшается в е раз.
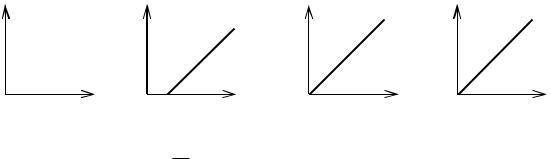
21. Реологическому поведению идеально вязкого тела Ньютона соответствует зависимость:
А) y |
|
Б) |
dy |
В) |
dy |
Г) y |
|
dт |
dт |
|
|||
|
|
|
|
|
||
|
|
|
|
|
|
|
P P P P
(y – величина деформации; dy – скорость деформации; Р – механическое dт
напряжение).
22. Реологическое поведение идеально упругого тела Гука отражает зависимость:
113