7.13 Применение производной второго порядка к исследованию функции

График функции называется выпуклым на интервале, если он расположен ниже касательной, проведенной к кривой в любой точке этого интервала (рис. 3.7)

y=ƒ(x)

0 a b x

Рис. 7.7 График функции, выпуклой на (a;b)

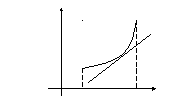
График функции называется вогнутым на интервале, если он расположен выше касательной, проведенной к кривой в любой точке этого интервала (рис. 7.8).

y y=ƒ(

ƒна (a;b)

ƒ′′(x)>0

0 a b x

Рис. 7.8 График функции вогнутой на (a;b)

Теорема (Достаточное условие выпуклости (вогнутости) графика функции). Пусть функция дважды дифференцируема на интервале. Если ƒ′′(х) <0 на (a;b), то график функции выпуклый на (a;b); если ƒ′′(х)>0 на (a;b), то график функции вогнутый на (a;b).

Точкой перегиба называется точка графика функции, отделяющая его выпуклую часть от вогнутой, и наоборот. (рис. 3.9)

y=ƒ(x)

ƒ′′( x₀)=0

0 x₀ x

Рис. 7.9 Точка перегиба графика функции

Теорема (необходимое условие точки перегиба). Если х₀ – точка перегиба графика функции y=ƒ(x) и существует вторая производная в ней, то ƒ′′( х₀)=0.

Точки, в которых вторая производная функции равна нулю, называются критическими точками второго рода.

Критические точки могут и не быть точками перегиба.

Теорема (Достаточное условие точки перегиба). Если вторая производная дважды дифференцируемой функции при переходе через критическую точку второго рода х₀ меняет знак, то х₀ есть абсцисса точки перегиба графика этой функции.

Пример:

7.30 Найти интервалы выпуклости (вогнутости) и точки перегиба графика функции

ƒ(х)=3х³+2х²-7х+2

Решение:

Находим вторую производную:

ƒ′(х)=9х²+4х-7;

ƒ′′(х)=18х+4.

Критические точки второго рода:

ƒ′′(х)=0 => 18х+4 =

Знак ƒ′′(х):

- +

ƒ′′(х)>0 на интервале , следовательно график функции вогнутна этом интервале; ƒ′′(х)<0 на интервале, следовательно, график функции выпуклна этом интервале. При переходе через критическую точку второго рода ƒ′′(х) меняет знак, следовательно,- абсцисса точки перегиба.