7.6 Производная обратной функции

Если функция ƒ(х), х є (а;b), и её обратная функция ƒ^-1(y); y₀= ƒ(x₀), имеют производные, то

(ƒ^-1(y₀))´= .(3.7)

Опуская значения аргументов, получаем:

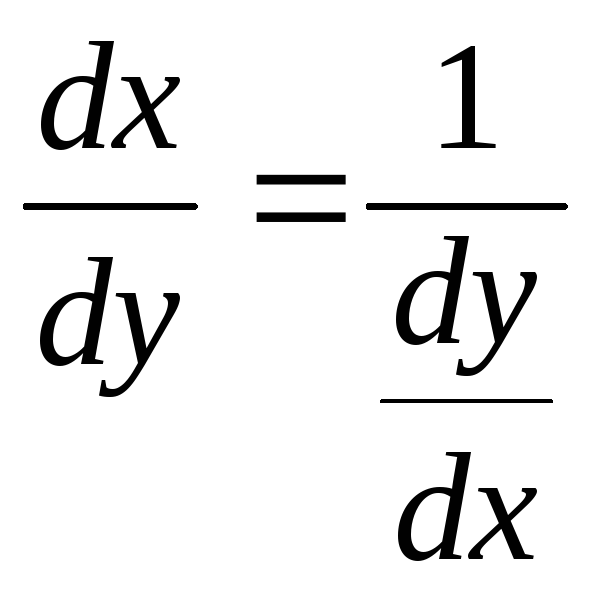или .

7.7 Таблица производных

C’=0; C=const

Правила дифференцирования:

Найти производные следующих функций, применяя таблицу производных и правила дифференцирования.

Пример:

7.6 Используем формулу

(хⁿ)´=nx^n-1

а) (х²)´=2х; б) (х³)´=3х²; в) (5х²+5х+7)´= 5·2х+5=10х+5;

г) при вычислении применяли формулы элементарной математики:

; ;

д) ;

е) найдем производную произведения по формуле (7.4)

((sinx)·e^x)´=(sinx)´· e^x +sin(e^x)´= cosx e^x +sinx e^x= e^x (cosx+sinx);

ж) найдем производную частного по формуле (7.5) .

Упражнения:

7.7 а) y= 3х³- 4х²+5х=7;

б) y= 2х²-6х+7;

в) ;

г) ;

д) ;

е) ;

ж) ;

з) ;

и) y= х²∙lnx;

к) y= (x³+1)arcsinx;

л) y= 2^x·cosx;

м) y= e^x·arccosx;

н) ;

o) .

Найти производные сложных функций по формуле (7.6)

Пример:

7.8 а)(sin2x)´=(cos2x)·(2x)´=(cos2x)·2=2cos2x;

в) ;

б) (sin3x)´=3cos3x;

г) .

Упражнения:

7.9 а) y= cos2x; y= cos3x; y=cos½x; y= cos(2x+3).

Пример:

7.10 Используем формулу:

; u=u(x).

.

Упражнения:

7.11 а) ;

б) ;

в) ;

г) .

Пример:

7.12 Используем формулу:

; u=u(x)

.

Упражнения:

7.13 а) ;

б) ;

в) ;

г) .

Примеры:

7.14 Используем формулу:

; u=u(x)

.

Упражнения:

7.15 а) y= ln tgx;

б) y= ln arcsinx;

в) y= ln(x²+3x+4);

г) y= ln2^x .

Пример:

7.15 Используем формулу

; u=u(x)

.

Упражнения:

7.16 а) y= log₃sinx;

б) y= log₂ctgx;

в) y= log₅(x²+1);

г) y= lg tgx.

Пример:

7.17 Используем формулу

; u=U(x)

(3^х²)´= 3^х²·(ln3)·2x.

Упражнения:

7.18 а) y= 3^х²+4х ;

б) y= 3^sinx;

в) y= 3^arcsinx;

г) y= 10^arccosx.

Пример:

7.19 Использовать формулы

(sin u)´= u´·cos u; u=U(x)

(cos u)´= u´·sin u

а)

б)

в)

г)

Упражнения:

7.20 а) y = sin cosx;

б) y = cos log₂x;

в) y = tg arcsinx;

г) .

Упражнения:

7.21 а) ;

б) ;

в) ;

г) ;

д) ;

е) ;

ж) ;

з) ;

7.8 Производные высших порядков

Рассмотрим функцию y=ƒ(x). Пусть существует производная y´=ƒ´(x) (производная первого порядка); ƒ´(x) также является функцией от х, пусть её можно дифференцировать. Получим производную, которая называется производной второго порядка:

y´´= (y´)´=(ƒ´(x))´=ƒ´´(x)

Аналогично находится производная третьего порядка:

y´´´= (y´´)´=ƒ´´´(x),

Производная n-го порядка:

y⁽ⁿ⁾= (y^(n-1))´=ƒ⁽ⁿ⁾(x)

Пример:

7.22 Найти y´´´, если y= sinx

Решение: Находим последовательно

y´= cosx; y´´= -sinx; y´´´= -cosx.

Упражнения:

7.23 Найти y^IV, если:

а) y= cosx;

б) y= 3x⁵+2x⁴-x²+1;

в) y= e^x;

г) .