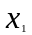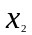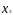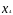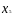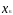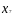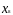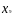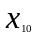Практики / п1
.docxФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ УФИМСКИЙ ГОСУДАРСТВЕННЫЙ АВИАЦИОННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра технической кибернетики
ОТЧЕТ по практической работе по теме: «Проверка гипотезы о положении центра группирования»
по дисциплине: «Основы теории надежности программных средств ВТ и АС»
Вариант – 23
Выполнил: ст. гр. ИВТ-325Б
Колязов К.А.
Проверил: профессор кафедры ТК
Гвоздев В. Е.
Уфа 2022
Практическая работа №1
Проверка гипотезы о положении центра группирования
Цель работы
Изучение методики проверки гипотезы о равенстве эмпирического центра группирования некоторому теоретическому значению.
Задание на работу
По данным таблицы,
приведенной в приложении 2, определить,
насколько
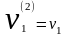 ,
где значение
,
где значение
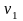 равно номеру варианта задания.
равно номеру варианта задания.
Номер варианта |
|
|
|
|
|
|
|
|
|
|
23 |
18,105 |
30,376 |
28,680 |
21,944 |
16,072 |
20,955 |
22,283 |
24,270 |
21,799 |
25,040 |
= 23;
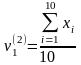 =22,952
=22,952
Найдем среднее квадратическое отклонение средней арифметической:
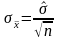 ,где
,где
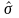 - эмпирическая оценка среднеквадратического
отклонения;
- эмпирическая оценка среднеквадратического
отклонения;
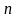 – объем выборки;
– объем выборки;
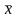 - оценка центра группирования.
- оценка центра группирования.
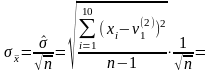 0,582
0,582
Поскольку гипотеза,
конкурирующая с нулевой, состоит в том,
что
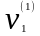
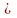
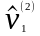 ,
то выберем в качестве критической
область, определяемую соотношением:
,
то выберем в качестве критической
область, определяемую соотношением:
|
-
| >
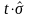 ,
где t
определяется соотношением:
,
где t
определяется соотношением:
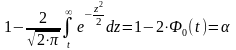
Здесь
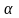 – уровень значимости проверки гипотезы
(определяется в процентах);
– уровень значимости проверки гипотезы
(определяется в процентах);
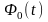 – нормированная функция Лапласа.
– нормированная функция Лапласа.
Возьмем уровень значимости =5%, тогда значение t будет равным
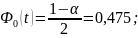
t=1,96.
Таким образом критическая область будет задана неравенством:
| - 23| > 1,96*0,582= 1,142.
Подставляя
значение
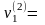 22,952
получаем |22,952-23|=0,048<1,142, что лежит вне
критической области, следовательно,
нет оснований для того, чтобы отвергнуть
гипотезу о равенстве центров группирования.
22,952
получаем |22,952-23|=0,048<1,142, что лежит вне
критической области, следовательно,
нет оснований для того, чтобы отвергнуть
гипотезу о равенстве центров группирования.
Вывод: в ходе данной практической работы была изучена методика проверки гипотезы о равенстве эмпирического центра группирования некоторому теоретическому значению.