
Практикум БСМП Scilab
.pdfСеменова Т.И., Шакин В.Н., Загвоздкина А.В.
Базовые средства математического пакета
Практикум
Москва, 2019 г.
1
Scilab – это математический пакет прикладных программ, предназначенный для численных вычислений и являющийся в этом направлении свободно распространяемым аналогом пакета Matlab. Пакет Scilab версии 6.01, изучению которого посвящен данный практикум, доступен на официальном сайте www.scilab.org.
Данный практикум, может быть использован при изучении различных дисциплин, связанных с численными расчетами при решении прикладных задач. Его целью является – познакомить студентов с назначением основных окон Scilab, элементами меню и содержащихся в них команд, с работой по созданию в Командном окне и текстовом редакторе функций пользователя, операциями над матрицами, возможностью визуализации результатов вычислений и многими другими возможностями Scilab. При этом особое внимание отводится средствам программирования, без которых не может быть выполнен практически ни один сложный расчет.
Материал данного практикума ориентирован на решение задач, носящих вычислительный характер, поэтому большая часть предлагаемых работ посвящена решению вычислительных задач средствами Scilab. В Scilab численные методы реализованы в виде множества встроенных функций, доступных пользователю в ходе проведения расчета. Форматы всех, используемых при выполнении лабораторных работ, функций описаны в учебнике[], а также в справочной системе[], встроенной в Scilab, обращение к которой может быть произведено с использованием соответствующего элемента меню или из командной строки.
Данный лабораторный практикум содержит 6 лабораторных работ:
1.Рабочая среда Scilab и простейшие вычисления.
2.Файловая система Scilab, Редактор SciNotes, sce-сценарии, вводвывод данных.
3.Матрицы – создание, доступ, матричные операции и функции.
4.Построение двумерных и трехмерных графиков.
5.Средства программирования в Scilab.
6.Интегрирование и дифференцирование средствами Scilab.
2
1. Основы работы с математическим пакетом Scilab
1.1. Лабораторная работа по теме «Рабочая среда Scilab и простейшие вычисления»
1.1.1.Вопросы, подлежащие изучению
1)Рабочая среда Scilab и ее элементы.
2)Правила работы в Командном окне.
3)Назначение основных окон рабочей среды: Обозревателя переменных ,Журнала команд и Обозревателя файлов при работе
вКомандном окне.
4)Установка свойств Рабочая среда системы Scilab.
5)Основные объекты системы Scilab.
6)Правила записи и вычисления арифметических выражений.
7)Создание и использование встроенных функциями пользователя при вычислении выражений.
1.1.2.Общее задание
1)Изучите материал учебника (п.п. 1.1-1.2).
2)Выберите вариант индивидуального задания из табл. 1.1-1.
3)При выполнении задания вводите перед каждым пункта задания соответствующие комментарии.
4)Задайте переменным x и yдопустимые числовые значения.
5)Проанализируйте информацию, возникшую в окне Обозреватель
переменных.
6)Введите формулу для вычислений арифметического выражения и получите результат.
7)Измените значения исходных данных.
8)Измените формат вывода результата, выполнив команду format(16), и произведите перерасчет значения выражения.
9)Измените формат вывода данных format(6).
10)Представьте арифметическое выражение в виде правой части функции f(x).
11)Опишите функциюf(x)с помощью оператора deff и вычислите
её числовое значение при новом значении переменной х.
12)Опишите функцию f1(x) с помощью оператора function.
13)Измените значение переменной y, выедите на экран значения описанного в п.10 выражения и функцииf1(x).
3

14)Объясните, почему изменение значения y не привело к изменению значения арифметического выражения, но повлияло на значение функции.
15)Задайте диапазон изменения аргумента функции с шагом,
позволяющим получить таблицу значений функции f(x) и f1(x)для заданных значений аргумента (порядка 8-10 точек), выведете значения функции f(х) в выбранном диапазоне вначале в строку, а затем в столбец.
16)Выполните команду who_user и проанализируйте выведенную
информацию о данных.
17)Сохраните текст рабочего окна на внешнем носителе в Word
18)Предоставьте результаты работы преподавателю и, ответьте на поставленные вопросы.
19)Выполните команды clear и clc для очистки Рабочей среды.
20)Оформите отчет по выполненной работе.
1.1.3.Варианты индивидуальных заданий
Таблица 1.1-1
|
№ |
|
|
|
|
|
|
|
|
|
|
|
|
|
Формулы для |
|
|
№ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Формулы для |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вычислений |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вычислений |
|
||||||||||||||||||||||
|
1. |
|
|
t |
cos |
|
π |
|
|
sin2 (x 8y) |
|
|
|
|
|
|
|
16. |
|
|
b |
|
lg x sin2 xy |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
7 |
|
|
|
|
|
2,7(x π) |
|
|
|
|
|
|
|
|
|
|
|
|
0,8 ln(1 x)2 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
2. |
|
|
|
|
|
|
|
|
(1 exy )2 |
|
|
|
|
|
|
|
|
|
|
|
17. |
|
|
|
|
|
|
|
|
|
|
|
|
2y |
|
|
|
|
|
|
3 |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
10 |
4 |
|
|
e |
|
|
| sin y | |
|
||||||||||||||
|
|
|
|
|
|
|
0,7lg |
1 x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2,5cos2 x |
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
3. |
|
|
h |
|
|
xy sin x |
|
|
|
|
|
|
|
|
|
|
|
18. |
|
|
|
π |
ln x3 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
1 y |
|
ln x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
3 |
|
|
|
|
|
|
|
|
|
x sin y2 |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3y x |
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
4. |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
19. |
|
|
|
|
208 lg x x2 |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
с |
|
|
(yx |
|
|
|
|
|
|
|
1) |
(cos2 y sin x2 ) |
|
|
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
x y2 |
e y |
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
5. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
||
|
|
|
b |
|
|
|
x y |
|
sin(tg2x) |
|
|
|
|
|
|
|
|
|
|
|
|
105 lg |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
0.8x |
e2xy |
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
0,2x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
6. |
|
|
d |
|
|
|
xexy 8 sin2 x |
|
|
|
|
|
|
|
21. |
|
|
b |
|
|
|
|
|
xy |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
x(x y)(3x y) |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
е |
x sin y |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
7. |
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x y2 |
|
|
|
|
|
|
22. |
|
|
c x lg |
|
x |
6 |
|
|
sin x2 |
|
|||||||||||||||||||||
|
|
|
z |
|
|
|
|
|
|
|
2x |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
0,75tg |
x |
y |
|
|
|
|
|
|
|
|
yx3 |
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
8. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
23. |
|
|
|
|
14 sin x y |
2 |
|
|
|
|
|
||||||||||||||||||
|
|
|
d |
|
xy |
2 |
|
|
|
|
x |
2 |
2,5 |
10 |
3 |
y |
0.5 |
|
|
|
|
a |
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2sin xy |
|
|
|
|
|
|
|
|
|
|
|
0.92 cos3 x |
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
9. |
|
|
f |
5,23 |
|
|
|
|
|
|
|
lg(x y) |
|
|
|
|
0.5 |
|
|
24. |
|
|
a |
|
|
|
|
|
|
x2 -xy |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
x |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.7sinln|x| |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0,45 sin(x 8y) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
10. |
|
|
a |
|
|
0,8 10 5 (xe x( y 1,2) yx)3 |
|
|
25. |
|
|
c |
|
2.71x2 cos y |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tg(x2 ) e y |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
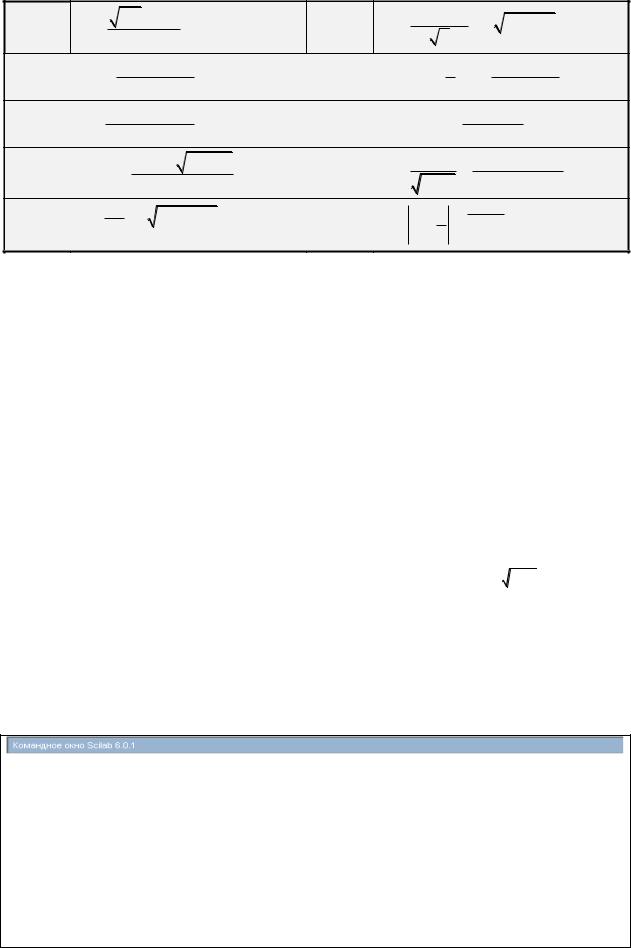
11. |
d |
| x | e |
y |
|
|
|
|
|
26. |
d |
1 tgxy |
2 |
4 x2 0,1 |
|||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
12. |
5,8 cos y3 |
|
|
|
|
|
27. |
|
3 x |
|
|
|
|
|||||||
f |
2x |
2 |
sin x |
2 |
|
|
|
|
f |
0.5 1 |
cos 1 sin xy |
2 |
||||||||
|
|
|
|
|
|
|
|
|
||||||||||||
13. |
|
|
2 e y |
|
|
|
|
|
28. |
|
2 |
|
|
1 sin2 xy |
||||||
h |
3 |
|
x e |
sin y |
|
|
|
|
g |
x e y |
|
2 |
|
|||||||
|
sin |
|
|
|
|
|
|
|
|
|
(x y) |
|
||||||||
14. |
|
0,6x2 y2 |
|
|
|
|
|
29. |
|
|
|
2 cos3 x |
|
|||||||
|
|
ln y2 4 | x y | |
|
|
z |
x y |
|
|
xy2 |
|
||||||||||
|
a |
10 |
|
|
|
1 cos3 y |
|
|
|
x y |
|
sin x2 cos2 y |
||||||||
15. |
|
1 |
|
|
|
|
|
|
|
3 |
|
3 |
|
30. |
|
π x e |
1 sin e y |
|
||
|
c |
2π x |
2,5 10 |
|
y | cos x |
|
| |
|
b |
2x |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
1.1.4. Содержание отчета |
|
|
|
|
||||||||
1) В начале сессии введите в формате комментариев:
xназвание лабораторной работы;
xФИО студента, номер группы;
x№ варианта;
xиндивидуальное задание.
2)Протокол вычислений (сессии) в Командном окне в соответствии с общим заданием, снабженный подробными комментариями.
1.1.5.Пример выполнения задания
1)Пример индивидуального задания.
Решить задачу вычисления арифметического выражения z |
x |
|
x y |
|
|
cos y2 в |
|
|
|
||||||
e |
x y |
2 |
|
|
|||
|
|
ln x |
|
|
|||
соответствии с п.п.3-15 общего задания.
2) Результат выполнения задания.
Протокол сессии в Командном окне:
-->//Практическое занятие 1.1 по теме
-->//«Рабочая среда Scilab и простейшие вычисления»
-->// Вариант 0
-->// Выполнил:Студент группы БИН1801 Иванов И.И.
-->
-->clear // Очистка окна Обозревателя данных
-->clc // Очистка Командного окна
-->//Задание начальных значений x и y -->x=4.55;
5

-->y=1.5;
-->// Ввод арифметического выражения
-->z=(x+sqrt(abs(x*y)))/(exp(x+y)*log(x)^2)-cos(y^2)
z=
0.6355303 -->//Изменение значенийx и y -->x=8.8;y=5.5;
-->//Изменение формата вывода результата
-->format(16); -->//Перерасчет выражения
-->z=(x+sqrt(abs(x*y)))/(exp(x+y)*log(x)^2)-cos(y^2)
z=
-0.3938970292202 -->format(6);
-->//Описание функцииfd с использованием deff
-->
-->deff('f1 = fd(x)','f1 = (x+sqrt(abs(x.*y)))./…
(exp(x+y).*log(x).^2)-cos(y.^2)'); -->
-->//Вызов функцииfdи вычисление ее значения
-->f1=fd(x) f1 =
- 0.394
-->//Описаниефункции ff с использованием function
-->
-->function [f2]=ff(x)
>f2 = (x+sqrt(abs(x.*y)))./(exp(x+y).*log(x).^2)-cos(y.^2); >end
-->
-->//Вызов функции ffи вычисление ее значения
-->f2=ff(x) f2 =
- 0.394 -->//Изменение значенияy -->y=0.1;
-->//Вычисление значения выражения при новомзначении y -->z
z=
- 0.394
-->//Вычисление значения функции ffпри новом значении y -->f2=ff(x)
f2 =
- 1.000
-->//Задание диапазона изменения переменной x -->x=2:0.2:3.8
x=
2. 2.2 2.4 2.6 2.8 3. 3.23.4 3.6 3.8
-->// Вычисление функции fd для заданного диапазона аргумента и
6

-->// вывод полученного результата в строку
-->fd(x) ans =
column 1 to 5
-0.376 -0.570 -0.690 -0.771 -0.827 column 6to 10
-0.868 -0.897 -0.920 -0.937 -0.950
-->// Вычисление функции ff для заданного диапазона аргумента х
-->//вывод в столбец
-->ff(x)' ans = -0.376
-0.570 -0.690 -0.771 -0.827 -0.868 -0.897 -0.920 -0.937 -0.950
--> // Конец сессии ========================================================
1.1.6.Контрольные вопросы по теме
1)Что является основными элементами Рабочей среды Scilab?
2)Каково назначение Командного окна?
3)Каково назначение окна Журнал команд?
4)Каково назначение окна Обозревателя переменных?
5)Каково назначение окна Обозреватель файлов?
6)Как установить текущий каталог в окне Обозреватель файлов?
7)Как установить Конфигурацию рабочего окна?
8)Как называется сеанс работы с пакетом Scilab в Командном окне?
9)Каким образом перенести командную строку из окна Журнал команд в окно Командное окно?
10)Каким образом изменить значение переменной в окне
Обозревателя переменных?
11)Для чего предназначен редактор SciNotes?
12)Как выбрать тип, размер и стиль шрифта в Командном окне?
13)Для чего используется Справочная система Scilab?
14)Как вызвать окно Справочной системы с использованием меню
иосуществить поиск нужной команды?
15)Какой командой вызывается справка из командного окна?
7
16)Что происходит, если, находясь в командной строке, нажать клавишу<↑> или <↓>?
17)Какой символ предназначен для запрета вывода результата выполнения действия на экран?
18)Какой символ служит для переноса части командной строки на следующую строку?
19)Какой формат имеет оператор описания функции deff?
20)Какой формат имеет оператор описания функции function?
21)В каких случаях используется оператор deff, а в каких function?
8
1.2. Лабораторная работа по теме
«Файловая система Scilab, Редактор SciNotes, sce-сценарии, ввод-вывод данных»
1.2.1.Вопросы, подлежащие изучению
1)Файловая система Scilab и Текущая папка.
2)Встроенный текстовый Редактор SciNotes.
3)Типы программных файлов.
4)Sce-сценарии.
5)Сохранение, вызов и выполнение сценария, сохраненного в sce.файле.
6)Cохранение и восстановление переменных Рабочей области.
7)Простейшие операторы ввода/вывода данных.
1.2.2.Общее задание
1)Изучите материал учебника (п. 1.5).
2)Выберете вариант индивидуального задания из табл. 1.2-1.
3)Выполните команды clear и clc для очистки окна Обозревателя переменных и Командного окна.
4)Активизируйте Редактор SciNotes.
5)Создайте sce-сценарий для выполнения индивидуального задания с использованием встроенных функций.
6)Сохраните sce-сценарий в sce-файле со смысловым именем.
7)Проведите отладку сценария и исправьте ошибки.
8)Загрузите sce-сценарий из sce-файла и выполните его в Командном окне, предварительно присвоив исходным данным допустимые значения.
9)Cохраните переменные Рабочей области, обнулите Рабочую область, а затем восстановите.
10)Модернизируйте sce-сценарий, вставив в него операторы ввода исходных данных и вывода результата.
11)Сохраните sce-сценарий под другим именем, исправьте ошибки и
выполните.
12)Сохраните все результаты для отчета.
13)Предоставьте результаты работы преподавателю, ответьте на поставленные вопросы.
14)Оформите отчет по выполненной работе.
9

1.2.3. Варианты индивидуальных заданий
Таблица 1.2-1
|
1 |
|
|
b |
|
π |
x |
|
e |
1 sin e y |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
2x |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
|
|
x2 y2 8sin( x y) cos( x y) |
|
|||||||||||||||||||||||||
|
2 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
c |
x |
2,5 103 y | cos x3 | |
|
|||||||||||||||||||||||||||
|
|
|
|
2π |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin2 (x y) 0.5ex sin( y) |
|
|||||||||||||||||
|
|
|
|
f |
|
x2 |
2 y2 |
|
|||||||||||||||||||||||||
|
3 |
|
|
|
|
|
|
|
|
ln y2 4 |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
a |
10 |
| x y | |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
1 cos3 y |
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
f |
|
x3 2 y2 sin( x y) cos(x y) x 2 y |
|
||||||||||||||||||||||||||
|
4 |
|
|
z |
|
x y |
|
|
|
|
|
|
|
xy |
2 |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
x y |
|
|
|
|
|
|
|
sin x2 cos2 y |
|
||||||||||||||||
|
|
|
|
f |
|
x3 2 y2 sin( x y) cos(x y) x 2 y |
|
||||||||||||||||||||||||||
|
5 |
|
|
h |
sin3 x e sin y |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,6x2 y2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
f 3 |
|
|
x3 2 y3 8sin( x y) cos(x y) 5x |
|
|||||||||||||||||||||||||
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||
|
|
|
|
g |
x e y |
|
|
(x y) |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
2 cos3 x |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
f |
|
3x3 y2 cos(x y) x 2x 9xy |
|
||||||||||||||||||||||||||
|
7 |
|
|
f |
|
2x |
2 |
|
sin x |
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 e y |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
f |
|
x2 |
2 y2 |
sin2 (x y) 0.5ex sin( y) |
|
||||||||||||||||||||||||
|
8 |
|
|
f |
0.5 |
1 |
cos |
1 sin xy |
2 |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
1 sin2 xy |
|
||||||||||
|
|
|
|
f |
3x3 y2 cos(x y) x 2 y 9xy ex cos( y) |
|
|||||||||||||||||||||||||||
|
9 |
|
|
f |
0.5 |
1 |
cos |
1 sin xy |
2 |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
1 sin2 xy |
|
||||||||||
|
|
|
|
f |
3x3 y2 cos(x y) x 2 y 9xy ex cos( y) |
|
|||||||||||||||||||||||||||
|
10 |
|
|
|
1 tgxy |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
d |
|
|
4 x2 0,1 |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
3 x |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
f |
3x3 y2 cos(x y) x 2 y 9xy |
|
|||||||||||||||||||||||||||
|
11 |
|
|
a |
0,8 10 5 (xe x( y 1,2) yx)3 |
|
|||||||||||||||||||||||||||
|
|
|
|
f |
|
x3 y2 x sin2 (x y) 2 y 9xy |
|
||||||||||||||||||||||||||
|
12 |
|
|
c |
2.71x2 cos y |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
tg(x2 ) e y |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
||
