
С2. МОИ. Презентации / Булевы функции 6 (v. 1.1)
.pdf
Задача минимизации схем из ф. э.
Доказательство. Выбор h функциональных элементов можно осуществить не более, чем
.r h способами. При этом p выходов схемы и входы функциональных элементов (а их не более, чем h ) присоединяются либо ко входам схемы либо к выходам функциональных элементов. Вариантов для этих подключений не более, чем (n +h) h +p. В результате получаем утверждение леммы.
 71
71

Функции Шеннона
Далее будем рассматривать задачу синтеза схем, реализующих булевы функции, т.е.
схем, имеющих n входов и p = 1 выходов.
Пусть S f – схема, реализующая булеву функцию f. Обозначим через
L( f ) min L(S f ), |
L(n) max L( f ). |
S f |
f P(n) |
|
2 |
 72
72

Функции Шеннона
Пусть А – некоторый алгоритм синтеза схем,
реализующих булевы функции, а LA ( f ) – сложность схемы, построенной алгоритмом
А и реализующей булеву функцию f. Обозначим через
LA (n) max LA ( f ).
f P2(n)
 73
73

Функции Шеннона
Пусть А – некоторый алгоритм синтеза схем,
реализующих булевы функции, а LA ( f ) – сложность схемы, построенной алгоритмом
А и реализующей булеву функцию f. Обозначим через
LA (n) max LA ( f ). |
|
|
f P(n) |
|
2 |
L( f ) LA ( f ) |
L(n) LA(n) |
 74
74

Элементарные методы синтеза схем из функциональных элементов
 75
75

I. Синтез, основанный на СДНФ
 76
76

Синтез, основанный на СДНФ
f x , x |
,..., x |
|
|
x |
|
|
|
|
n |
|
1 |
... x |
|
|
|||||||
1 2 |
n |
|
(1,..., n) |
1 |
|
n |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
f (1,..., n)1
w( f )
i 1 Ki
 77
77

Синтез, основанный на СДНФ
x1 x2 . . . xn
|
|
|
|
|
|
|
|
|
|
w( f ) |
|
|
|
x |
|
|
K |
|
|||||
f (x , x ,..., x ) |
|
... x |
|
|
|
|
|||||
|
1 |
|
n |
|
i |
||||||
1 2 |
n |
( 1,..., n) |
1 |
n |
|
|
i 1 |
||||
|
|
|
|
|
|
|
|
|
|
||
|
|
f ( 1,..., n) 1 |
|
|
|
|
|
|
|
78 |
|

Синтез, основанный на СДНФ
x1 x2 . . . xn
|
|
|
|
|
|
|
|
|
|
w( f ) |
|
|
|
x |
|
|
K |
|
|||||
f (x , x ,..., x ) |
|
... x |
|
|
|
|
|||||
|
1 |
|
n |
|
i |
||||||
1 2 |
n |
( 1,..., n) |
1 |
n |
|
|
i 1 |
||||
|
|
|
|
|
|
|
|
|
|
||
|
|
f ( 1,..., n) 1 |
|
|
|
|
|
|
|
79 |
|
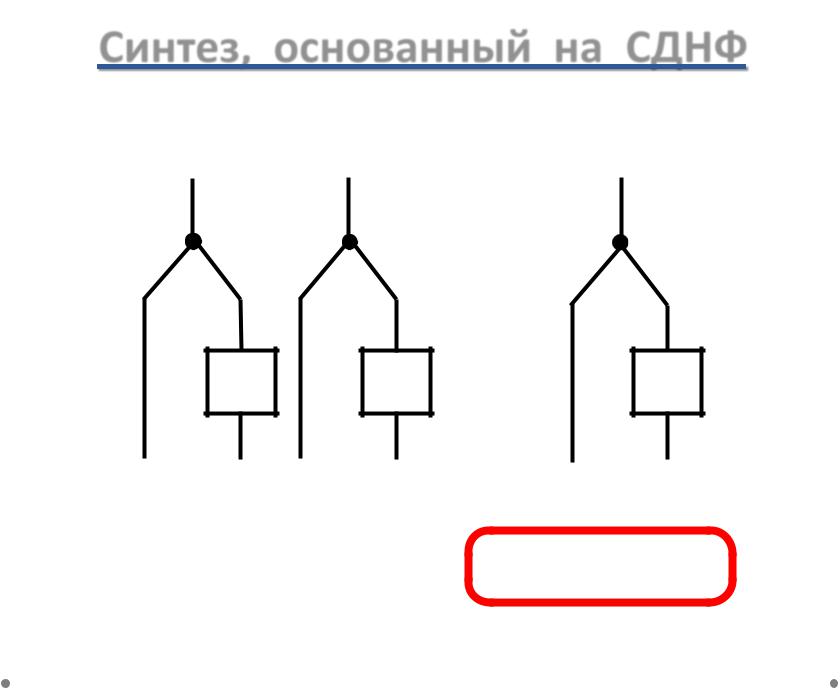
Синтез, основанный на СДНФ
x1 |
x2 |
. . . xn |
|
. . . |
|
|
|
|
|
|
|
|
|
|
|
w( f ) |
|
|
|
x |
|
|
K |
|
|||||
f (x , x ,..., x ) |
|
... x |
|
|
|
|
|||||
|
1 |
|
n |
|
i |
||||||
1 2 |
n |
( 1,..., n) |
1 |
n |
|
|
i 1 |
||||
|
|
|
|
|
|
|
|
|
|
||
|
|
f ( 1,..., n) 1 |
|
|
|
|
|
|
|
80 |
|
